Karatay, Caratal River, Axonopus fissifolius

କରାଟେ: କରାଟାଇ କିମ୍ବା କରାଟାଇ ହେଉଛି ଏକ ତୁର୍କୀ ଶବ୍ଦ ଯାହା ସୂଚାଇପାରେ :
କରାଟାଲ୍ ନଦୀ: କରାଟାଲ୍ ନଦୀ ହେଉଛି ସେଣ୍ଟ ଭିନ୍ସେଣ୍ଟ ଏବଂ ଗ୍ରେନାଡାଇନ୍ସର ଏକ ନଦୀ |
ଆକ୍ସୋନୋପସ୍ ଫିସିଫୋଲିୟସ୍: ଆକ୍ସୋନୋପସ୍ ଫିସିଫୋଲିୟସ୍ ହେଉଛି ଏକ ଘାସ ପ୍ରଜାତି ଯାହା ପ୍ରାୟତ permanent ସ୍ଥାୟୀ ଚାରଣଭୂମି ଭାବରେ ବ୍ୟବହୃତ ହୁଏ |
କାରାଟାସ୍କା ଲାଗୁନ୍: ଉତ୍ତର-ପୂର୍ବ ହୋଣ୍ଡୁରାସର ଗ୍ରାସିଆସ୍ ଏକ ଡାୟୋସ୍ ବିଭାଗରେ କାରାଟାସ୍କା ଲାଗୁନ୍ ଏକ ବଡ଼ ଲାଗୁନ୍ | ବିଭାଗର ରାଜଧାନୀ ପୁଏରୋ ଲେମ୍ପିରା ଏହାର କୂଳରେ ଅବସ୍ଥିତ।
କାରାଟାଉନାସ୍: କାରାଟାଉନାସ୍ ହେଉଛି ସ୍ପେନର ଗ୍ରାନାଡା ପ୍ରଦେଶରେ ଅବସ୍ଥିତ ଏକ ପ ity ରପାଳିକା | 2005 ଜନଗଣନା (INE) ଅନୁଯାୟୀ ଏହାର ଜନସଂଖ୍ୟା 198 ବାସିନ୍ଦା |
କାରାଟାଉନାସ୍: କାରାଟାଉନାସ୍ ହେଉଛି ସ୍ପେନର ଗ୍ରାନାଡା ପ୍ରଦେଶରେ ଅବସ୍ଥିତ ଏକ ପ ity ରପାଳିକା | 2005 ଜନଗଣନା (INE) ଅନୁଯାୟୀ ଏହାର ଜନସଂଖ୍ୟା 198 ବାସିନ୍ଦା |
କାରାଟାଉନାସ୍: କାରାଟାଉନାସ୍ ହେଉଛି ସ୍ପେନର ଗ୍ରାନାଡା ପ୍ରଦେଶରେ ଅବସ୍ଥିତ ଏକ ପ ity ରପାଳିକା | 2005 ଜନଗଣନା (INE) ଅନୁଯାୟୀ ଏହାର ଜନସଂଖ୍ୟା 198 ବାସିନ୍ଦା |
କରାଟେ: କ୍ୟାରେଟ୍ ରେଫର୍ କରିପାରେ:
କ୍ୟାରେଟ୍-କାଲୋ ରେଳ ଷ୍ଟେସନ୍: କ୍ୟାରେଟ୍-କାଲୋ ରେଳ ଷ୍ଟେସନ୍ ହେଉଛି ଇଟାଲୀର ଏକ ରେଳ ଷ୍ଟେସନ୍ | ମୋଞ୍ଜା - ମଲଟେନୋ ରେଳପଥରେ ଅବସ୍ଥିତ, ଏହା ଲୋମ୍ବର୍ଡିରେ କରାଟେ ପ municipal ରପାଳିକାକୁ ସେବା କରେ | ଟ୍ରେନ୍ ସେବାଗୁଡିକ ଟ୍ରେନୋର୍ଡ ଦ୍ୱାରା ପରିଚାଳିତ |
କରାଟେ: କ୍ୟାରେଟ୍ ରେଫର୍ କରିପାରେ:
ପିଣ୍ଟା (ରୋଗ): ପିଣ୍ଟା ହେଉଛି ଏକ ମାନବ ଚର୍ମ ରୋଗ, ଯାହା ସ୍ପିରୋଚେଟ୍ , ଟ୍ରେପୋନେମା କାରାଟେମ୍ ସହିତ ସଂକ୍ରମଣ ଦ୍ caused ାରା ହୋଇଥାଏ , ଯାହା ସିଫିଲିସ୍ ସୃଷ୍ଟି କରୁଥିବା ବ୍ୟାକ୍ଟେରିଆରୁ morphological ଏବଂ serologic ଭିନ୍ନ ନୁହେଁ। ଏହି ରୋଗ ମେକ୍ସିକୋ, ମଧ୍ୟ ଆମେରିକା ଏବଂ ଦକ୍ଷିଣ ଆମେରିକା ପାଇଁ ଏଣ୍ଡେମିକ୍।
କରାଟେ ବିମାନବନ୍ଦର: କରାଟେ ବିମାନବନ୍ଦର ହେଉଛି କୋଷ୍ଟାରିକାର ଓସା ଉପଦ୍ୱୀପରେ ସାଇରେନାର ଉପକୂଳ ଗନ୍ତବ୍ୟସ୍ଥଳକୁ ସେବା କରୁଥିବା ଏକ କଂକ୍ରିଟ୍ ଏୟାରଷ୍ଟ୍ରିପ୍ | ଏହି ବିମାନବନ୍ଦର ମୁଖ୍ୟତ S ସାଇରେନା ଟାଉନ୍ ଏବଂ କର୍କୋଭାଡୋ ଜାତୀୟ ଉଦ୍ୟାନ ନିକଟରେ ଥିବା ପର୍ଯ୍ୟଟକମାନଙ୍କ ସହିତ ଚାର୍ଟର୍ ସେବା ଦ୍ୱାରା ବ୍ୟବହୃତ ହୋଇଥାଏ | ବର୍ତ୍ତମାନ ବିମାନବନ୍ଦରରେ ଅନ୍ୟ କ from ଣସି ବିମାନବନ୍ଦରରୁ ନିର୍ଧାରିତ ସେବା ନାହିଁ।
କରାଟେ ବ୍ରିଆଞ୍ଜା: Carate Brianza ର Monza ଏବଂ Brianza, Lombardy, ଉତ୍ତର ଇଟାଲି ପ୍ରେଦଶ ଏକ ସହର ଏବଂ comune ଅଟେ। ଏହି ସହର ଲମ୍ବ୍ରୋ ନଦୀ ଉପରେ ସମୁଦ୍ର ପତ୍ତନ ଠାରୁ 230 ରୁ 300 ମିଟର ଉଚ୍ଚରେ ଅବସ୍ଥିତ |
କ୍ୟାରେଟ୍ ମିଶ୍ରିତ ବନ୍ୟଜନ୍ତୁ ଶରଣାର୍ଥୀ: କ୍ୟାରେଟ୍ ମିକ୍ସଡ୍ ୱାଇଲ୍ଡ ଲାଇଫ୍ ରିଫ୍ୟୁଜ୍ , କୋଷ୍ଟାରିକାର ଏକ ସଂରକ୍ଷିତ ଅଞ୍ଚଳ, ଓସା ସଂରକ୍ଷଣ କ୍ଷେତ୍ର ଅଧୀନରେ ପରିଚାଳିତ, ଏହା 27471-MINAE ଆଦେଶ ଦ୍ 1998 ାରା 1998 ରେ ସୃଷ୍ଟି ହୋଇଥିଲା |
କ୍ୟାରେଟ୍ ଉରିଓ: କ୍ୟାରେଟ୍ ଉରିଓ ହେଉଛି ଇଟାଲୀର ଲୋମ୍ବାର୍ଡର କୋମୋ ପ୍ରଦେଶର ଏକ କମ୍ୟୁନିଟି ( ପ municipal ରପାଳିକା ), ମିଲାନ୍ର ଉତ୍ତରରେ ପ୍ରାୟ 45 କିଲୋମିଟର (28 ମାଇଲ୍) ଏବଂ କୋମୋ ଠାରୁ ପ୍ରାୟ 6 କିଲୋମିଟର (4 ମାଇଲ୍) ଉତ୍ତର-ପୂର୍ବରେ ଅବସ୍ଥିତ |
କନସୋ ଭାଷା: କୋନ୍ସୋ ହେଉଛି ଦକ୍ଷିଣ-ପଶ୍ଚିମ ଇଥିଓପିଆରେ କଥିତ ଏକ ନିମ୍ନଭୂମି କୁଶୀୟ ଭାଷା | କନସୋ ର ଦେଶୀ ବକ୍ତାମାନେ ପ୍ରାୟ 200,000 | କନସୋ ଦିରାଶା ସହିତ ନିବିଡ ଭାବରେ ଜଡିତ, ଏବଂ କନସୋ ଲୋକଙ୍କ ଅଞ୍ଚଳ ବାହାରେ ଏକ "ବାଣିଜ୍ୟ ଭାଷା" - କିମ୍ବା ଲିଙ୍ଗୁଆ ଫ୍ରାଙ୍କା ଭାବରେ କାର୍ଯ୍ୟ କରେ | ବ୍ଲେଞ୍ଚ (2006) ନିର୍ଦ୍ଦିଷ୍ଟ ଭାଷା ଗାଟୋ ଏବଂ ଟୁରୋକୁ ପୃଥକ ଭାଷା ଭାବରେ ବିବେଚନା କରେ |
କ୍ୟାରେଟିନ୍: କାରେଟେନ୍ ବରଗଡର ରାଜା ଗୁଣ୍ଡୋବାଦ୍ଙ୍କ ପତ୍ନୀ ଥିଲେ। ତାଙ୍କ ସ୍ୱାମୀଙ୍କ ପରି, ଯିଏ ଆରିୟାନ୍ ଥିଲେ, କ୍ୟାରେଟେନ୍ ଜଣେ କ୍ୟାଥୋଲିକ୍ ଥିଲେ | ସେ ବୋଧହୁଏ ବରଗଡର ସିଗିସମୁଣ୍ଡର ମାତା ଥିଲେ |
କରାଥିଆ: କାରାଥିଆ ମାଲକାରିଡା ପରିବାର ମଧ୍ୟରେ ତସମାନିଆ ସ୍ପାଇଡର ଏକ ବଂଶ ଯାହାକି 1986 ମସିହାରେ ଆରଜେ ମୋରାନଙ୍କ ଦ୍ named ାରା ନାମିତ ଏବଂ ବର୍ଣ୍ଣନା କରାଯାଇଥିଲା। ଏହି ନାମ ଅଷ୍ଟ୍ରେଲିଆର ଆଦିବାସୀ ଶବ୍ଦ "ଭଉଣୀ" ରୁ ଆସିଛି। ପ୍ରକାର ପ୍ରଜାତି ହେଉଛି C. parawea | ଏହି ବଂଶର ସ୍ପାଇଡର୍ ପାଇଁ ଅତୁଳନୀୟ ବ features ଶିଷ୍ଟ୍ୟଗୁଡିକ କଣ୍ଡକ୍ଟର ପାଇଁ ଏକ ପତଳା ଟିପ୍, କାରାପେସରେ "ଶିଙ୍ଗ" ର ଅନୁପସ୍ଥିତି, ଏବଂ ମହିଳାମାନଙ୍କ ମଧ୍ୟରେ ଆଭ୍ୟନ୍ତରୀଣ ଯ ital ନାଙ୍ଗ ବଡ଼ ଏବଂ କମ୍ କମ୍ପାକ୍ଟ, ସାଧାରଣତ only କେବଳ ତିନି କିମ୍ବା ଚାରି କୋଇଲ୍ ଧାରଣ କରିଥାଏ |
କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀ: କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀ ଜଣେ ଗ୍ରୀକ୍ ଗଣିତଜ୍ଞ ଥିଲେ ଯିଏକି ତାଙ୍କର ବୃତ୍ତିଗତ ବୃତ୍ତିର ଅଧିକାଂଶ ସମୟ ଜର୍ମାନୀରେ ବିତାଇଥିଲେ | ବାସ୍ତବ ଏବଂ ଜଟିଳ ବିଶ୍ଳେଷଣ, ଭିନ୍ନତାର ଗଣନା, ଏବଂ ମାପ ସିଦ୍ଧାନ୍ତରେ ସେ ମହତ୍ contributions ପୂର୍ଣ ଅବଦାନ ରଖିଥିଲେ | ସେ ଥର୍ମୋଡାଇନାମିକ୍ସର ଏକ ସ୍ୱୀକୃତିପ୍ରାପ୍ତ ସୂତ୍ର ମଧ୍ୟ ସୃଷ୍ଟି କରିଥିଲେ |
କାରାଥୋଡୋରିର ମାନଦଣ୍ଡ: କାରାଥୋଡୋରୀର ମାନଦଣ୍ଡ ହେଉଛି ମାପ ସିଦ୍ଧାନ୍ତର ଏକ ଫଳାଫଳ ଯାହା ଗ୍ରୀକ୍ ଗଣିତଜ୍ଞ କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀ ଦ୍ୱାରା ପ୍ରସ୍ତୁତ କରାଯାଇଥିଲା | ଏହାର ଷ୍ଟେଟମେଣ୍ଟ ନିମ୍ନରେ ଦିଆଯାଇଛି: ଚାଲ | ଲେବସ୍ଗେ ବାହ୍ୟ ମାପକୁ ସୂଚିତ କରେ | , ଏବଂ ଦିଅନ୍ତୁ | । ତା'ପରେ ଯଦି ଏବଂ କେବଳ ଯଦି ଲେବେସଗୁ ମାପଯୋଗ୍ୟ | ପ୍ରତ୍ୟେକଙ୍କ ପାଇଁ , ର ସପ୍ଲିମେଣ୍ଟକୁ ଦର୍ଶାଉଛି | ଧ୍ୟାନ ଦିଅନ୍ତୁ | ଏକ ମାପଯୋଗ୍ୟ ସେଟ୍ ହେବା ଆବଶ୍ୟକ ନୁହେଁ |
କାରାଥୋଡୋରିର ଅସ୍ତିତ୍ୱ ଥିଓରେମ୍: ଗଣିତରେ, କାରାଥୋଡୋରିର ଅସ୍ତିତ୍ୱ ଥିଓରେମ୍ କହିଛି ଯେ ସାମାନ୍ୟ ଭିନ୍ନ ଅବସ୍ଥାରେ ଏକ ସାଧାରଣ ଡିଫେରିଏଲ୍ ସମୀକରଣର ସମାଧାନ ଅଛି | ଏହା Peano ର ଅସ୍ତିତ୍ୱ ଥିଓରେମର ଏକ ସାଧାରଣକରଣ | ପିଆନୋଙ୍କ ଥିଓରେମ୍ ଆବଶ୍ୟକ କରେ ଯେ ଡିଫେରିଏଲ୍ ସମୀକରଣର ଡାହାଣ ପାର୍ଶ୍ୱ ନିରନ୍ତର ରହିବା ଆବଶ୍ୟକ, ଯେତେବେଳେ କି କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ କିଛି ବିଚ୍ଛିନ୍ନ ସମୀକରଣ ପାଇଁ ସମାଧାନର ଅସ୍ତିତ୍ୱ ଦେଖାଏ | ଥିଓରେମ୍ କନଷ୍ଟାଣ୍ଟିନ୍ କାରାଥୋଡୋରୀଙ୍କ ନାମରେ ନାମିତ |
କାରାଥୋଡୋରୀର ବିସ୍ତାର ତତ୍ତ୍ୱ: ମାପ ତତ୍ତ୍ୱ ରେ, Carathéodory ର ବିସ୍ତୃତକରଣ theorem ରାଜ୍ୟ ଯେ R ଦ୍ଵାରା ଆୟୋଜିତ σ-algebra ଉପରେ ଏକ ମାପ ପାଇଁ କୌଣସି ପୂର୍ବରୁ ମାପ ଏକ ପ୍ରଦତ୍ତ ସେଟ୍ Ω ଉପସେଟ ଏକ ପ୍ରଦତ୍ତ ମୁଦି R ଉପରେ ବ୍ୟାଖ୍ୟା ଅନୁଲମ୍ବିତ କରାଯାଇପାରିବ, ଏବଂ ଏହି ବିସ୍ତୃତକରଣ ଯଦି pre- ଅନନ୍ୟ ଅଟେ ମାପ ହେଉଛି σ- ସୀମିତ | ଫଳସ୍ୱରୂପ, ପ୍ରକୃତ ସଂଖ୍ୟାଗୁଡ଼ିକର ସମସ୍ତ ବ୍ୟବଧାନ ଧାରଣ କରିଥିବା ଏକ ରିଙ୍ଗ ଉପରେ ଯେକ any ଣସି ପୂର୍ବ-ମାପ ପ୍ରକୃତ ସଂଖ୍ୟା ସେଟ୍ ର ବୋରେଲ୍ ବୀଜ ବର୍ଣ୍ଣିତକୁ ବିସ୍ତାର କରାଯାଇପାରେ | ମାପ ସିଦ୍ଧାନ୍ତର ଏହା ଏକ ଅତ୍ୟନ୍ତ ଶକ୍ତିଶାଳୀ ଫଳାଫଳ, ଏବଂ ଉଦାହରଣ ସ୍ୱରୂପ, ଲେବେସଗୁ ମାପକୁ ନେଇଥାଏ |
ବାହ୍ୟ ମାପ: ମାପ ତତ୍ତ୍ of ର ଗାଣିତିକ କ୍ଷେତ୍ରରେ, ଏକ ବାହ୍ୟ ମାପ ବା ବାହ୍ୟ ମାପ ହେଉଛି ଏକ କାର୍ଯ୍ୟ ଯାହାକି ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ସେଟ୍ ର ସମସ୍ତ ସବ୍ସେଟରେ ବ୍ୟାଖ୍ୟା କରାଯାଇଥାଏ ଯାହାକି ବର୍ଦ୍ଧିତ ପ୍ରକୃତ ସଂଖ୍ୟାରେ ମୂଲ୍ୟ ସହିତ କିଛି ଅତିରିକ୍ତ ବ technical ଷୟିକ ଅବସ୍ଥା ପୂରଣ କରେ | ମାପ କରାଯାଉଥିବା ସେଟ୍ ଏବଂ ଗଣନାତ୍ମକ ଭାବରେ ଯୋଗୀ ପଦକ୍ଷେପଗୁଡ଼ିକର ତତ୍ତ୍ for ପାଇଁ ଏକ ଅବଷ୍ଟ୍ରାକ୍ଟ ଆଧାର ଯୋଗାଇବା ପାଇଁ ପ୍ରଥମେ କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀ ଦ୍ୱାରା ବାହ୍ୟ ପଦକ୍ଷେପଗୁଡ଼ିକର ସିଦ୍ଧାନ୍ତ ପ୍ରବର୍ତ୍ତିତ ହୋଇଥିଲା | ବାହ୍ୟ ପଦକ୍ଷେପ ଉପରେ କାରାଥୋଡୋରିଙ୍କ କାର୍ଯ୍ୟ ମାପ-ଥିଓରେଟିକ୍ ସେଟ୍ ସିଦ୍ଧାନ୍ତରେ ଅନେକ ପ୍ରୟୋଗ ପାଇଲା, ଏବଂ ହାଉସଡର୍ଫ ଦ୍ by ାରା ଏକ ଡାଇମେନ୍ସନ୍ ପରି ମେଟ୍ରିକ୍ ଇନଭାରିଅଣ୍ଟକୁ ବର୍ତ୍ତମାନ ହାଉସଡର୍ଫ୍ ଡାଇମେନ୍ସନ୍ ଭାବରେ ବ୍ୟାଖ୍ୟା କରିବାକୁ ଏକ ଜରୁରୀ ଉପାୟରେ ବ୍ୟବହୃତ ହୋଇଥିଲା | ଜ୍ୟାମିତିକ ମାପ ସିଦ୍ଧାନ୍ତ କ୍ଷେତ୍ରରେ ବାହ୍ୟ ମାପ ସାଧାରଣତ used ବ୍ୟବହୃତ ହୁଏ |
ଥର୍ମୋଡାଇନାମିକ୍ସର ଦ୍ୱିତୀୟ ନିୟମ: ଥର୍ମୋଡାଇନାମିକ୍ସର ଦ୍ୱିତୀୟ ନିୟମ ଥର୍ମୋଡାଇନାମିକ୍ ସିଷ୍ଟମର ଭ physical ତିକ ସମ୍ପତ୍ତି ଭାବରେ ଏଣ୍ଟ୍ରପି ଧାରଣାକୁ ସ୍ଥାପିତ କରେ | ଏଣ୍ଟ୍ରପି ସ୍ୱତ aneous ପ୍ରବୃତ୍ତ ପ୍ରକ୍ରିୟାର ଦିଗ ପୂର୍ବାନୁମାନ କରେ ଏବଂ ଶକ୍ତି ସଂରକ୍ଷଣର ଆବଶ୍ୟକତା ପାଳନ କରିବା ସତ୍ତ୍ they େ ସେଗୁଡିକ ପ୍ରତ୍ୟାବର୍ତ୍ତନଯୋଗ୍ୟ କିମ୍ବା ଅସମ୍ଭବ କି ନୁହେଁ ତାହା ସ୍ଥିର କରେ, ଯାହା ଥର୍ମୋଡାଇନାମିକ୍ସର ପ୍ରଥମ ନିୟମରେ ପ୍ରତିଷ୍ଠିତ | ଦ୍ law ିତୀୟ ନିୟମ ପର୍ଯ୍ୟବେକ୍ଷଣ ଦ୍ ulated ାରା ପ୍ରସ୍ତୁତ କରାଯାଇପାରେ ଯେ ସ୍ ont ତ aneous ସ୍ପୃତ ବିବର୍ତ୍ତନକୁ ଛାଡି ଦିଆଯାଇଥିବା ପୃଥକ ସିଷ୍ଟମର ଏଣ୍ଟ୍ରପି ହ୍ରାସ ହୋଇପାରିବ ନାହିଁ, କାରଣ ସେମାନେ ସର୍ବଦା ଥର୍ମୋଡାଇନାମିକ୍ ସନ୍ତୁଳନ ସ୍ଥିତିରେ ପହଞ୍ଚନ୍ତି, ଯେଉଁଠାରେ ଏଣ୍ଟ୍ରପି ସର୍ବାଧିକ | ଯଦି ସିଷ୍ଟମରେ ଥିବା ସମସ୍ତ ପ୍ରକ୍ରିୟା ଓଲଟା, ଏଣ୍ଟ୍ରପି ସ୍ଥିର ଅଟେ | ପ୍ରାକୃତିକ ପ୍ରକ୍ରିୟାଗୁଡ଼ିକର ପ୍ରତ୍ୟାବର୍ତ୍ତନ ପାଇଁ ଏଣ୍ଟ୍ରପି ଆକାଉଣ୍ଟଗୁଡିକର ବୃଦ୍ଧି, ସମୟର ତୀର ଧାରାରେ ପ୍ରାୟତ referred କୁହାଯାଏ |
କାରାଥୋଡୋରୀଙ୍କ ଥିଓରେମ୍: ଗଣିତରେ, କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀର ଅନେକ ଫଳାଫଳ ମଧ୍ୟରୁ ଗୋଟିଏକୁ ସୂଚାଇପାରେ: ସୀମା ପର୍ଯ୍ୟନ୍ତ କନଫର୍ମାଲ୍ ମ୍ୟାପିଂର ବିସ୍ତାର ବିଷୟରେ କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ | ଇଉକ୍ଲିଡିଆନ୍ ସ୍ପେସରେ ସେଟ୍ ର କନଭକ୍ସ ହଲ୍ ବିଷୟରେ କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ | ସାଧାରଣ ଡିଫେରିଏଲ୍ ସମୀକରଣର ସମାଧାନର ଅସ୍ତିତ୍ about ବିଷୟରେ କାରାଥୋଡୋରୀର ଅସ୍ତିତ୍ୱ ଥିଓରେମ୍ | ଏକ ମାପର ବିସ୍ତାର ବିଷୟରେ କାରାଥୋଡୋରୀର ବିସ୍ତାର ତତ୍ତ୍। | ଏକ ଜଟିଳ ଆନାଲିଟିକ୍ କାର୍ଯ୍ୟର ସୀମା ବିଷୟରେ ବୋରେଲ୍ - କାରାଥୋଡୋରୀ ଥିଓରେମ୍ | କାରାଥୋଡୋରୀ - ଜାକୋବି - ମିଛ ଥିଓରେମ୍, ସିମ୍ପ୍ଲେକ୍ଟିକ୍ ଟପୋଲୋଜିରେ ଡାରବକ୍ସଙ୍କ ଥିଓରେମର ଏକ ସାଧାରଣକରଣ | କାରାଥୋଡୋରୀର ମାନଦଣ୍ଡ, ଏକ ମାପଯୋଗ୍ୟ ସେଟ୍ ପାଇଁ ଏକ ଆବଶ୍ୟକୀୟ ଏବଂ ପର୍ଯ୍ୟାପ୍ତ ସର୍ତ୍ତ | କାରାଥୋଡୋରୀ କର୍ଣ୍ଣଲ ଥିଓରେମ୍, ଅସମାନ କାର୍ଯ୍ୟଗୁଡ଼ିକର ସ୍ଥାନୀୟ ୟୁନିଫର୍ମ ସମ୍ମିଶ୍ରଣ ପାଇଁ ଏକ ଜ୍ୟାମିତିକ ମାନଦଣ୍ଡ |
କାରାଥୋଡୋରିର ଥିଓରେମ୍ (କନଫର୍ମାଲ୍ ମ୍ୟାପିଙ୍ଗ୍): ଗଣିତରେ, କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ ହେଉଛି ଜଟିଳ ବିଶ୍ଳେଷଣରେ ଏକ ଥିଓରେମ୍, କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀଙ୍କ ନାମରେ ନାମିତ, ଯାହା ରିମାନ୍ ମ୍ୟାପିଙ୍ଗ୍ ଥିଓରେମ୍ ବିସ୍ତାର କରେ | 1913 ରେ ପ୍ରଥମେ ପ୍ରମାଣିତ ହୋଇଥିବା ଥିଓରେମ୍ରେ ଦର୍ଶାଯାଇଛି ଯେ ଜୋର୍ଡାନ ବକ୍ର ଦ୍ୱାରା ସୀମିତ ଜଟିଳ ବିମାନରେ ୟୁନିଟ୍ ଡିସ୍କକୁ ପଠାଉଥିବା କନଫର୍ମାଲ୍ ମ୍ୟାପିଙ୍ଗ୍ କ୍ରମାଗତ ଭାବରେ ୟୁନିଟ୍ ସର୍କଲରୁ ଜୋର୍ଡାନ ବକ୍ର ପର୍ଯ୍ୟନ୍ତ ଏକ ହୋମିଓମୋର୍ଫିଜିମ୍ ପର୍ଯ୍ୟନ୍ତ ବିସ୍ତାର କରିଥାଏ | ଫଳାଫଳ ହେଉଛି ପ୍ରଧାନ ଶେଷରେ କାରାଥୋଡୋରୀର ଫଳାଫଳ ଏବଂ ଅସମାନ ହୋଲୋମୋର୍ଫିକ୍ କାର୍ଯ୍ୟଗୁଡ଼ିକର ସୀମା ଆଚରଣ |
କାରାଥୋଡୋରିର ଥିଓରେମ୍ (କନଭକ୍ସ ହଲ୍): କାରାଥେଡୋରିର ଥିଓରେମ୍ ହେଉଛି କନଭକ୍ସ ଜ୍ୟାମିତିର ଏକ ଥିଓରେମ୍ | ଏହା ହେଉଛି ସବୁଠାରୁ d + 1 ଯଥା ପି ରେ ପଦକ୍ଷେପରେ ଏକ ସେଟ୍ P ର convex Hull ରେ R d ମିଥ୍ଯା ର ଏକ ବିନ୍ଦୁ x, ତେବେ x ର convex ସମଷ୍ଟି ଭାବରେ ଲେଖାଯାଇପାରିବ ଯଦି େସଠାେର ଅଛନ୍ତି P ଏକ ଉପସେଟ୍ P 'ଗଠିତ ଆମେରିକାନ୍ d + 1 କିମ୍ବା କମ୍ ପଏଣ୍ଟଗୁଡିକ ଯେପରିକି x P ର କନଭକ୍ସ ହଲ୍ ରେ ଅଛି | ସମାନ ଭାବରେ, x ଏକ R- ସିମ୍ପ୍ଲେକ୍ସରେ P ରେ ଥିବା ଭର୍ଟିକ୍ସ ସହିତ ଅଛି, ଯେଉଁଠାରେ | । କ୍ଷୁଦ୍ର r ଯାହାକି P ର କନଭକ୍ସ ହଲ୍ ରେ ପ୍ରତ୍ୟେକ x ପାଇଁ ଶେଷ ଷ୍ଟେଟମେଣ୍ଟକୁ ବ valid ଧ କରେ , କାରାଥୋଡୋରୀର P ସଂଖ୍ୟା ଭାବରେ ବ୍ୟାଖ୍ୟା କରାଯାଇଛି | P ର ଗୁଣ ଉପରେ ନିର୍ଭର କରି, କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ ଦ୍ୱାରା ପ୍ରଦତ୍ତ ସୀମାଠାରୁ କମ୍ ଉପର ସୀମା ମିଳିପାରିବ | ଧ୍ୟାନ ଦିଅନ୍ତୁ ଯେ P ନିଜେ କନଭକ୍ସ ହେବା ଆବଶ୍ୟକ ନୁହେଁ | ଏହା ଏକ ପରିଣାମ ଯେ P 'ସର୍ବଦା ହୋଇପାରେ P ରେ extremal, ଭାବରେ ଅଣ-extremal ବିନ୍ଦୁ convex Hull ରେ X ର ସଦସ୍ୟତା ପରିବର୍ତ୍ତନ ନକରି P ଅପସାରିତ ହୋଇପାରିବ ହେଉଛି।
କାରାଥୋଡୋରୀଙ୍କ ଥିଓରେମ୍: ଗଣିତରେ, କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀର ଅନେକ ଫଳାଫଳ ମଧ୍ୟରୁ ଗୋଟିଏକୁ ସୂଚାଇପାରେ: ସୀମା ପର୍ଯ୍ୟନ୍ତ କନଫର୍ମାଲ୍ ମ୍ୟାପିଂର ବିସ୍ତାର ବିଷୟରେ କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ | ଇଉକ୍ଲିଡିଆନ୍ ସ୍ପେସରେ ସେଟ୍ ର କନଭକ୍ସ ହଲ୍ ବିଷୟରେ କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ | ସାଧାରଣ ଡିଫେରିଏଲ୍ ସମୀକରଣର ସମାଧାନର ଅସ୍ତିତ୍ about ବିଷୟରେ କାରାଥୋଡୋରୀର ଅସ୍ତିତ୍ୱ ଥିଓରେମ୍ | ଏକ ମାପର ବିସ୍ତାର ବିଷୟରେ କାରାଥୋଡୋରୀର ବିସ୍ତାର ତତ୍ତ୍। | ଏକ ଜଟିଳ ଆନାଲିଟିକ୍ କାର୍ଯ୍ୟର ସୀମା ବିଷୟରେ ବୋରେଲ୍ - କାରାଥୋଡୋରୀ ଥିଓରେମ୍ | କାରାଥୋଡୋରୀ - ଜାକୋବି - ମିଛ ଥିଓରେମ୍, ସିମ୍ପ୍ଲେକ୍ଟିକ୍ ଟପୋଲୋଜିରେ ଡାରବକ୍ସଙ୍କ ଥିଓରେମର ଏକ ସାଧାରଣକରଣ | କାରାଥୋଡୋରୀର ମାନଦଣ୍ଡ, ଏକ ମାପଯୋଗ୍ୟ ସେଟ୍ ପାଇଁ ଏକ ଆବଶ୍ୟକୀୟ ଏବଂ ପର୍ଯ୍ୟାପ୍ତ ସର୍ତ୍ତ | କାରାଥୋଡୋରୀ କର୍ଣ୍ଣଲ ଥିଓରେମ୍, ଅସମାନ କାର୍ଯ୍ୟଗୁଡ଼ିକର ସ୍ଥାନୀୟ ୟୁନିଫର୍ମ ସମ୍ମିଶ୍ରଣ ପାଇଁ ଏକ ଜ୍ୟାମିତିକ ମାନଦଣ୍ଡ |
ବାହ୍ୟ ମାପ: ମାପ ତତ୍ତ୍ of ର ଗାଣିତିକ କ୍ଷେତ୍ରରେ, ଏକ ବାହ୍ୟ ମାପ ବା ବାହ୍ୟ ମାପ ହେଉଛି ଏକ କାର୍ଯ୍ୟ ଯାହାକି ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ସେଟ୍ ର ସମସ୍ତ ସବ୍ସେଟରେ ବ୍ୟାଖ୍ୟା କରାଯାଇଥାଏ ଯାହାକି ବର୍ଦ୍ଧିତ ପ୍ରକୃତ ସଂଖ୍ୟାରେ ମୂଲ୍ୟ ସହିତ କିଛି ଅତିରିକ୍ତ ବ technical ଷୟିକ ଅବସ୍ଥା ପୂରଣ କରେ | ମାପ କରାଯାଉଥିବା ସେଟ୍ ଏବଂ ଗଣନାତ୍ମକ ଭାବରେ ଯୋଗୀ ପଦକ୍ଷେପଗୁଡ଼ିକର ତତ୍ତ୍ for ପାଇଁ ଏକ ଅବଷ୍ଟ୍ରାକ୍ଟ ଆଧାର ଯୋଗାଇବା ପାଇଁ ପ୍ରଥମେ କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀ ଦ୍ୱାରା ବାହ୍ୟ ପଦକ୍ଷେପଗୁଡ଼ିକର ସିଦ୍ଧାନ୍ତ ପ୍ରବର୍ତ୍ତିତ ହୋଇଥିଲା | ବାହ୍ୟ ପଦକ୍ଷେପ ଉପରେ କାରାଥୋଡୋରିଙ୍କ କାର୍ଯ୍ୟ ମାପ-ଥିଓରେଟିକ୍ ସେଟ୍ ସିଦ୍ଧାନ୍ତରେ ଅନେକ ପ୍ରୟୋଗ ପାଇଲା, ଏବଂ ହାଉସଡର୍ଫ ଦ୍ by ାରା ଏକ ଡାଇମେନ୍ସନ୍ ପରି ମେଟ୍ରିକ୍ ଇନଭାରିଅଣ୍ଟକୁ ବର୍ତ୍ତମାନ ହାଉସଡର୍ଫ୍ ଡାଇମେନ୍ସନ୍ ଭାବରେ ବ୍ୟାଖ୍ୟା କରିବାକୁ ଏକ ଜରୁରୀ ଉପାୟରେ ବ୍ୟବହୃତ ହୋଇଥିଲା | ଜ୍ୟାମିତିକ ମାପ ସିଦ୍ଧାନ୍ତ କ୍ଷେତ୍ରରେ ବାହ୍ୟ ମାପ ସାଧାରଣତ used ବ୍ୟବହୃତ ହୁଏ |
କାରାଥୋଡୋରୀ - ଜାକୋବି - ମିଥ୍ୟା ତତ୍ତ୍ୱ: କାରାଥୋଡୋରୀ - ଜାକୋବି - ମିଛ ଥିଓରେମ୍ ହେଉଛି ସିମ୍ପଲେକ୍ଟିକ୍ ଜ୍ୟାମିତିର ଏକ ଥିଓରେମ୍ ଯାହା ଡାରବକ୍ସଙ୍କ ଥିଓରେମ୍ କୁ ସାଧାରଣ କରିଥାଏ |
କାରାଥୋଡୋରୀ- π ସମାଧାନ: ଏକ କାରାଥୋଡୋରୀ- π ସମାଧାନ ହେଉଛି ଏକ ସାଧାରଣ ଭିନ୍ନ ଭିନ୍ନ ସମୀକରଣର ଏକ ସାଧାରଣ ସମାଧାନ | ଏହି ଧାରଣା I. ମାଇକେଲ ରସଙ୍କ କାରଣରୁ ହୋଇଛି ଏବଂ କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀ ସମ୍ମାନରେ ନାମିତ | ଏହାର ବ୍ୟବହାରିକତା 2008 ରେ ରସ୍ ଏଟ୍ ଦ୍ୱାରା ପ୍ରଦର୍ଶିତ ହୋଇଥିଲା | ଧାରଣାର ଏକ ଲାବୋରେଟୋରୀ କାର୍ଯ୍ୟାନ୍ୱୟନରେ | ମତାମତ ନିୟନ୍ତ୍ରଣକୁ କାର୍ଯ୍ୟକାରୀ କରିବା ପାଇଁ ଏହି ଧାରଣାଟି ଅତ୍ୟନ୍ତ ଉପଯୋଗୀ, ବିଶେଷତ Ross ରସଙ୍କ ସିଉଡୋସ୍ପେକ୍ଟ୍ରାଲ୍ ଅପ୍ଟିମଲ୍ କଣ୍ଟ୍ରୋଲ୍ ସିଦ୍ଧାନ୍ତର ଏକ ପ୍ରୟୋଗ ଦ୍ୱାରା ଉତ୍ପନ୍ନ |
କାରାଥୋଡୋରୀ ଧାରଣା: ଡିଫେରିଏଲ୍ ଜ୍ୟାମିତ୍ରୀରେ , କାରାଥୋଡୋରୀ ଧାରଣା ହେଉଛି ଏକ ଗାଣିତିକ ଧାରଣା ଯାହାକି 1924 ମସିହାରେ ବର୍ଲିନ୍ ଗଣିତ ସୋସାଇଟିର ଏକ ଅଧିବେଶନରେ ହାନ୍ସ ଲୁଡୱିଗ୍ ହେମ୍ବର୍ଗର୍ଙ୍କ ଦ୍ୱାରା କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀ ଦ୍ୱାରା ଦର୍ଶାଯାଇଥିଲା। ଏଥିରେ, ଜନ୍ ଏଡେନ୍ସର୍ ଲିଟିଲଉଡ୍ ଏକ ଗାଣିତିକ ଦାବିର ଉଦାହରଣ ଭାବରେ ଧାରଣା ଏବଂ ହାମବର୍ଗର ଅବଦାନ ବିଷୟରେ ଉଲ୍ଲେଖ କରିଛନ୍ତି ଯାହା କହିବା ସହଜ କିନ୍ତୁ ପ୍ରମାଣ କରିବା କଷ୍ଟକର | ବିମାନ ବକ୍ର ପାଇଁ ଫୋର୍ ଭର୍ଟେକ୍ସ ଥିଓରେମ୍ ସହିତ କନଜେକ୍ଟରର ଆନୁଷ୍ଠାନିକ ଅନୁରୂପରେ ଡିର୍କ ଷ୍ଟ୍ରିକ୍ ବର୍ଣ୍ଣନା କରିଛନ୍ତି | ଧାରଣାକୁ ଆଧୁନିକ ସନ୍ଦର୍ଭଗୁଡ଼ିକ ହେଉଛି ଶିଙ୍ଗ-ତୁଙ୍ଗ ୟାଙ୍କ ସମସ୍ୟା ତାଲିକା, ମାର୍ସେଲ ବର୍ଗର୍ଙ୍କ ପୁସ୍ତକ ଏବଂ ପୁସ୍ତକଗୁଡ଼ିକ |
କାରାଥୋଡୋରୀର ବିସ୍ତାର ତତ୍ତ୍ୱ: ମାପ ତତ୍ତ୍ୱ ରେ, Carathéodory ର ବିସ୍ତୃତକରଣ theorem ରାଜ୍ୟ ଯେ R ଦ୍ଵାରା ଆୟୋଜିତ σ-algebra ଉପରେ ଏକ ମାପ ପାଇଁ କୌଣସି ପୂର୍ବରୁ ମାପ ଏକ ପ୍ରଦତ୍ତ ସେଟ୍ Ω ଉପସେଟ ଏକ ପ୍ରଦତ୍ତ ମୁଦି R ଉପରେ ବ୍ୟାଖ୍ୟା ଅନୁଲମ୍ବିତ କରାଯାଇପାରିବ, ଏବଂ ଏହି ବିସ୍ତୃତକରଣ ଯଦି pre- ଅନନ୍ୟ ଅଟେ ମାପ ହେଉଛି σ- ସୀମିତ | ଫଳସ୍ୱରୂପ, ପ୍ରକୃତ ସଂଖ୍ୟାଗୁଡ଼ିକର ସମସ୍ତ ବ୍ୟବଧାନ ଧାରଣ କରିଥିବା ଏକ ରିଙ୍ଗ ଉପରେ ଯେକ any ଣସି ପୂର୍ବ-ମାପ ପ୍ରକୃତ ସଂଖ୍ୟା ସେଟ୍ ର ବୋରେଲ୍ ବୀଜ ବର୍ଣ୍ଣିତକୁ ବିସ୍ତାର କରାଯାଇପାରେ | ମାପ ସିଦ୍ଧାନ୍ତର ଏହା ଏକ ଅତ୍ୟନ୍ତ ଶକ୍ତିଶାଳୀ ଫଳାଫଳ, ଏବଂ ଉଦାହରଣ ସ୍ୱରୂପ, ଲେବେସଗୁ ମାପକୁ ନେଇଥାଏ |
କାରାଥୋଡୋରୀ କର୍ଣ୍ଣଲ ଥିଓରେମ୍: ଗଣିତରେ, 1912 ମସିହାରେ ଗ୍ରୀକ୍ ଗଣିତଜ୍ଞ କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀଙ୍କ ଦ୍ established ାରା ସ୍ଥାପିତ ଜଟିଳ ବିଶ୍ଳେଷଣ ଏବଂ ଜ୍ୟାମିତିକ ଫଙ୍କସନ୍ ସିଦ୍ଧାନ୍ତରେ କାରାଥୋଡୋରୀ କର୍ଣ୍ଣଲ ଥିଓରେମ୍ ହେଉଛି ଏକ ଫଳାଫଳ | ଏବଂ ଫିକ୍ସିଂ 0, କାର୍ଯ୍ୟଗୁଡ଼ିକର ପ୍ରତିଛବିଗୁଡ଼ିକର ସୀମିତ ଆଚରଣ ଦୃଷ୍ଟିରୁ ଜ୍ୟାମିତିକ ଭାବରେ ନିର୍ଦ୍ଧିଷ୍ଟ ହୋଇପାରିବ | ଅସମାନ କାର୍ଯ୍ୟଗୁଡ଼ିକର ସିଦ୍ଧାନ୍ତରେ କର୍ଣ୍ଣଲ ଥିଓରେମର ବ୍ୟାପକ ପ୍ରୟୋଗ ରହିଛି ଏବଂ ବିଶେଷ ଭାବରେ ଲୋଏନର୍ ଡିଫେରିଏଲ୍ ସମୀକରଣ ପାଇଁ ଜ୍ୟାମିତିକ ଆଧାର ପ୍ରଦାନ କରିଥାଏ |
ବାହ୍ୟ ମାପ: ମାପ ତତ୍ତ୍ of ର ଗାଣିତିକ କ୍ଷେତ୍ରରେ, ଏକ ବାହ୍ୟ ମାପ ବା ବାହ୍ୟ ମାପ ହେଉଛି ଏକ କାର୍ଯ୍ୟ ଯାହାକି ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ସେଟ୍ ର ସମସ୍ତ ସବ୍ସେଟରେ ବ୍ୟାଖ୍ୟା କରାଯାଇଥାଏ ଯାହାକି ବର୍ଦ୍ଧିତ ପ୍ରକୃତ ସଂଖ୍ୟାରେ ମୂଲ୍ୟ ସହିତ କିଛି ଅତିରିକ୍ତ ବ technical ଷୟିକ ଅବସ୍ଥା ପୂରଣ କରେ | ମାପ କରାଯାଉଥିବା ସେଟ୍ ଏବଂ ଗଣନାତ୍ମକ ଭାବରେ ଯୋଗୀ ପଦକ୍ଷେପଗୁଡ଼ିକର ତତ୍ତ୍ for ପାଇଁ ଏକ ଅବଷ୍ଟ୍ରାକ୍ଟ ଆଧାର ଯୋଗାଇବା ପାଇଁ ପ୍ରଥମେ କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀ ଦ୍ୱାରା ବାହ୍ୟ ପଦକ୍ଷେପଗୁଡ଼ିକର ସିଦ୍ଧାନ୍ତ ପ୍ରବର୍ତ୍ତିତ ହୋଇଥିଲା | ବାହ୍ୟ ପଦକ୍ଷେପ ଉପରେ କାରାଥୋଡୋରିଙ୍କ କାର୍ଯ୍ୟ ମାପ-ଥିଓରେଟିକ୍ ସେଟ୍ ସିଦ୍ଧାନ୍ତରେ ଅନେକ ପ୍ରୟୋଗ ପାଇଲା, ଏବଂ ହାଉସଡର୍ଫ ଦ୍ by ାରା ଏକ ଡାଇମେନ୍ସନ୍ ପରି ମେଟ୍ରିକ୍ ଇନଭାରିଅଣ୍ଟକୁ ବର୍ତ୍ତମାନ ହାଉସଡର୍ଫ୍ ଡାଇମେନ୍ସନ୍ ଭାବରେ ବ୍ୟାଖ୍ୟା କରିବାକୁ ଏକ ଜରୁରୀ ଉପାୟରେ ବ୍ୟବହୃତ ହୋଇଥିଲା | ଜ୍ୟାମିତିକ ମାପ ସିଦ୍ଧାନ୍ତ କ୍ଷେତ୍ରରେ ବାହ୍ୟ ମାପ ସାଧାରଣତ used ବ୍ୟବହୃତ ହୁଏ |
କାରାଥୋଡୋରୀ ମେଟ୍ରିକ୍: ଗଣିତରେ, କାରାଥୋଡୋରୀ ମେଟ୍ରିକ୍ ହେଉଛି ଏକ ମେଟ୍ରିକ୍ ଯାହା ଏକ ଜଟିଳ ବନାଚ୍ ସ୍ପେସ୍ ର ଖୋଲା ୟୁନିଟ୍ ବଲ୍ ଉପରେ ବ୍ୟାଖ୍ୟା କରାଯାଇଛି ଯାହାର ହାଇପରବୋଲିକ୍ ଜ୍ୟାମିତିର ପୋଇନାର୍ ମେଟ୍ରିକ୍ ସହିତ ଅନେକ ସମାନ ଗୁଣ ଅଛି | ଗ୍ରୀକ୍ ଗଣିତଜ୍ଞ କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀଙ୍କ ନାମରେ ଏହାର ନାମକରଣ କରାଯାଇଛି |
କାରାଥୋଡୋରୀଙ୍କ ଥିଓରେମ୍: ଗଣିତରେ, କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀର ଅନେକ ଫଳାଫଳ ମଧ୍ୟରୁ ଗୋଟିଏକୁ ସୂଚାଇପାରେ: ସୀମା ପର୍ଯ୍ୟନ୍ତ କନଫର୍ମାଲ୍ ମ୍ୟାପିଂର ବିସ୍ତାର ବିଷୟରେ କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ | ଇଉକ୍ଲିଡିଆନ୍ ସ୍ପେସରେ ସେଟ୍ ର କନଭକ୍ସ ହଲ୍ ବିଷୟରେ କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ | ସାଧାରଣ ଡିଫେରିଏଲ୍ ସମୀକରଣର ସମାଧାନର ଅସ୍ତିତ୍ about ବିଷୟରେ କାରାଥୋଡୋରୀର ଅସ୍ତିତ୍ୱ ଥିଓରେମ୍ | ଏକ ମାପର ବିସ୍ତାର ବିଷୟରେ କାରାଥୋଡୋରୀର ବିସ୍ତାର ତତ୍ତ୍। | ଏକ ଜଟିଳ ଆନାଲିଟିକ୍ କାର୍ଯ୍ୟର ସୀମା ବିଷୟରେ ବୋରେଲ୍ - କାରାଥୋଡୋରୀ ଥିଓରେମ୍ | କାରାଥୋଡୋରୀ - ଜାକୋବି - ମିଛ ଥିଓରେମ୍, ସିମ୍ପ୍ଲେକ୍ଟିକ୍ ଟପୋଲୋଜିରେ ଡାରବକ୍ସଙ୍କ ଥିଓରେମର ଏକ ସାଧାରଣକରଣ | କାରାଥୋଡୋରୀର ମାନଦଣ୍ଡ, ଏକ ମାପଯୋଗ୍ୟ ସେଟ୍ ପାଇଁ ଏକ ଆବଶ୍ୟକୀୟ ଏବଂ ପର୍ଯ୍ୟାପ୍ତ ସର୍ତ୍ତ | କାରାଥୋଡୋରୀ କର୍ଣ୍ଣଲ ଥିଓରେମ୍, ଅସମାନ କାର୍ଯ୍ୟଗୁଡ଼ିକର ସ୍ଥାନୀୟ ୟୁନିଫର୍ମ ସମ୍ମିଶ୍ରଣ ପାଇଁ ଏକ ଜ୍ୟାମିତିକ ମାନଦଣ୍ଡ |
କାରାଥୋଡୋରିର ଥିଓରେମ୍ (କନଫର୍ମାଲ୍ ମ୍ୟାପିଙ୍ଗ୍): ଗଣିତରେ, କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ ହେଉଛି ଜଟିଳ ବିଶ୍ଳେଷଣରେ ଏକ ଥିଓରେମ୍, କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀଙ୍କ ନାମରେ ନାମିତ, ଯାହା ରିମାନ୍ ମ୍ୟାପିଙ୍ଗ୍ ଥିଓରେମ୍ ବିସ୍ତାର କରେ | 1913 ରେ ପ୍ରଥମେ ପ୍ରମାଣିତ ହୋଇଥିବା ଥିଓରେମ୍ରେ ଦର୍ଶାଯାଇଛି ଯେ ଜୋର୍ଡାନ ବକ୍ର ଦ୍ୱାରା ସୀମିତ ଜଟିଳ ବିମାନରେ ୟୁନିଟ୍ ଡିସ୍କକୁ ପଠାଉଥିବା କନଫର୍ମାଲ୍ ମ୍ୟାପିଙ୍ଗ୍ କ୍ରମାଗତ ଭାବରେ ୟୁନିଟ୍ ସର୍କଲରୁ ଜୋର୍ଡାନ ବକ୍ର ପର୍ଯ୍ୟନ୍ତ ଏକ ହୋମିଓମୋର୍ଫିଜିମ୍ ପର୍ଯ୍ୟନ୍ତ ବିସ୍ତାର କରିଥାଏ | ଫଳାଫଳ ହେଉଛି ପ୍ରଧାନ ଶେଷରେ କାରାଥୋଡୋରୀର ଫଳାଫଳ ଏବଂ ଅସମାନ ହୋଲୋମୋର୍ଫିକ୍ କାର୍ଯ୍ୟଗୁଡ଼ିକର ସୀମା ଆଚରଣ |
କାରାଥୋଡୋରିର ଥିଓରେମ୍ (କନଭକ୍ସ ହଲ୍): କାରାଥେଡୋରିର ଥିଓରେମ୍ ହେଉଛି କନଭକ୍ସ ଜ୍ୟାମିତିର ଏକ ଥିଓରେମ୍ | ଏହା ହେଉଛି ସବୁଠାରୁ d + 1 ଯଥା ପି ରେ ପଦକ୍ଷେପରେ ଏକ ସେଟ୍ P ର convex Hull ରେ R d ମିଥ୍ଯା ର ଏକ ବିନ୍ଦୁ x, ତେବେ x ର convex ସମଷ୍ଟି ଭାବରେ ଲେଖାଯାଇପାରିବ ଯଦି େସଠାେର ଅଛନ୍ତି P ଏକ ଉପସେଟ୍ P 'ଗଠିତ ଆମେରିକାନ୍ d + 1 କିମ୍ବା କମ୍ ପଏଣ୍ଟଗୁଡିକ ଯେପରିକି x P ର କନଭକ୍ସ ହଲ୍ ରେ ଅଛି | ସମାନ ଭାବରେ, x ଏକ R- ସିମ୍ପ୍ଲେକ୍ସରେ P ରେ ଥିବା ଭର୍ଟିକ୍ସ ସହିତ ଅଛି, ଯେଉଁଠାରେ | । କ୍ଷୁଦ୍ର r ଯାହାକି P ର କନଭକ୍ସ ହଲ୍ ରେ ପ୍ରତ୍ୟେକ x ପାଇଁ ଶେଷ ଷ୍ଟେଟମେଣ୍ଟକୁ ବ valid ଧ କରେ , କାରାଥୋଡୋରୀର P ସଂଖ୍ୟା ଭାବରେ ବ୍ୟାଖ୍ୟା କରାଯାଇଛି | P ର ଗୁଣ ଉପରେ ନିର୍ଭର କରି, କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ ଦ୍ୱାରା ପ୍ରଦତ୍ତ ସୀମାଠାରୁ କମ୍ ଉପର ସୀମା ମିଳିପାରିବ | ଧ୍ୟାନ ଦିଅନ୍ତୁ ଯେ P ନିଜେ କନଭକ୍ସ ହେବା ଆବଶ୍ୟକ ନୁହେଁ | ଏହା ଏକ ପରିଣାମ ଯେ P 'ସର୍ବଦା ହୋଇପାରେ P ରେ extremal, ଭାବରେ ଅଣ-extremal ବିନ୍ଦୁ convex Hull ରେ X ର ସଦସ୍ୟତା ପରିବର୍ତ୍ତନ ନକରି P ଅପସାରିତ ହୋଇପାରିବ ହେଉଛି।
କାରାଥୋଡୋରୀଙ୍କ ଥିଓରେମ୍: ଗଣିତରେ, କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀର ଅନେକ ଫଳାଫଳ ମଧ୍ୟରୁ ଗୋଟିଏକୁ ସୂଚାଇପାରେ: ସୀମା ପର୍ଯ୍ୟନ୍ତ କନଫର୍ମାଲ୍ ମ୍ୟାପିଂର ବିସ୍ତାର ବିଷୟରେ କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ | ଇଉକ୍ଲିଡିଆନ୍ ସ୍ପେସରେ ସେଟ୍ ର କନଭକ୍ସ ହଲ୍ ବିଷୟରେ କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ | ସାଧାରଣ ଡିଫେରିଏଲ୍ ସମୀକରଣର ସମାଧାନର ଅସ୍ତିତ୍ about ବିଷୟରେ କାରାଥୋଡୋରୀର ଅସ୍ତିତ୍ୱ ଥିଓରେମ୍ | ଏକ ମାପର ବିସ୍ତାର ବିଷୟରେ କାରାଥୋଡୋରୀର ବିସ୍ତାର ତତ୍ତ୍। | ଏକ ଜଟିଳ ଆନାଲିଟିକ୍ କାର୍ଯ୍ୟର ସୀମା ବିଷୟରେ ବୋରେଲ୍ - କାରାଥୋଡୋରୀ ଥିଓରେମ୍ | କାରାଥୋଡୋରୀ - ଜାକୋବି - ମିଛ ଥିଓରେମ୍, ସିମ୍ପ୍ଲେକ୍ଟିକ୍ ଟପୋଲୋଜିରେ ଡାରବକ୍ସଙ୍କ ଥିଓରେମର ଏକ ସାଧାରଣକରଣ | କାରାଥୋଡୋରୀର ମାନଦଣ୍ଡ, ଏକ ମାପଯୋଗ୍ୟ ସେଟ୍ ପାଇଁ ଏକ ଆବଶ୍ୟକୀୟ ଏବଂ ପର୍ଯ୍ୟାପ୍ତ ସର୍ତ୍ତ | କାରାଥୋଡୋରୀ କର୍ଣ୍ଣଲ ଥିଓରେମ୍, ଅସମାନ କାର୍ଯ୍ୟଗୁଡ଼ିକର ସ୍ଥାନୀୟ ୟୁନିଫର୍ମ ସମ୍ମିଶ୍ରଣ ପାଇଁ ଏକ ଜ୍ୟାମିତିକ ମାନଦଣ୍ଡ |
ବାହ୍ୟ ମାପ: ମାପ ତତ୍ତ୍ of ର ଗାଣିତିକ କ୍ଷେତ୍ରରେ, ଏକ ବାହ୍ୟ ମାପ ବା ବାହ୍ୟ ମାପ ହେଉଛି ଏକ କାର୍ଯ୍ୟ ଯାହାକି ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ସେଟ୍ ର ସମସ୍ତ ସବ୍ସେଟରେ ବ୍ୟାଖ୍ୟା କରାଯାଇଥାଏ ଯାହାକି ବର୍ଦ୍ଧିତ ପ୍ରକୃତ ସଂଖ୍ୟାରେ ମୂଲ୍ୟ ସହିତ କିଛି ଅତିରିକ୍ତ ବ technical ଷୟିକ ଅବସ୍ଥା ପୂରଣ କରେ | ମାପ କରାଯାଉଥିବା ସେଟ୍ ଏବଂ ଗଣନାତ୍ମକ ଭାବରେ ଯୋଗୀ ପଦକ୍ଷେପଗୁଡ଼ିକର ତତ୍ତ୍ for ପାଇଁ ଏକ ଅବଷ୍ଟ୍ରାକ୍ଟ ଆଧାର ଯୋଗାଇବା ପାଇଁ ପ୍ରଥମେ କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀ ଦ୍ୱାରା ବାହ୍ୟ ପଦକ୍ଷେପଗୁଡ଼ିକର ସିଦ୍ଧାନ୍ତ ପ୍ରବର୍ତ୍ତିତ ହୋଇଥିଲା | ବାହ୍ୟ ପଦକ୍ଷେପ ଉପରେ କାରାଥୋଡୋରିଙ୍କ କାର୍ଯ୍ୟ ମାପ-ଥିଓରେଟିକ୍ ସେଟ୍ ସିଦ୍ଧାନ୍ତରେ ଅନେକ ପ୍ରୟୋଗ ପାଇଲା, ଏବଂ ହାଉସଡର୍ଫ ଦ୍ by ାରା ଏକ ଡାଇମେନ୍ସନ୍ ପରି ମେଟ୍ରିକ୍ ଇନଭାରିଅଣ୍ଟକୁ ବର୍ତ୍ତମାନ ହାଉସଡର୍ଫ୍ ଡାଇମେନ୍ସନ୍ ଭାବରେ ବ୍ୟାଖ୍ୟା କରିବାକୁ ଏକ ଜରୁରୀ ଉପାୟରେ ବ୍ୟବହୃତ ହୋଇଥିଲା | ଜ୍ୟାମିତିକ ମାପ ସିଦ୍ଧାନ୍ତ କ୍ଷେତ୍ରରେ ବାହ୍ୟ ମାପ ସାଧାରଣତ used ବ୍ୟବହୃତ ହୁଏ |
କାରାଥୋଡୋରୀ - ଜାକୋବି - ମିଥ୍ୟା ତତ୍ତ୍ୱ: କାରାଥୋଡୋରୀ - ଜାକୋବି - ମିଛ ଥିଓରେମ୍ ହେଉଛି ସିମ୍ପଲେକ୍ଟିକ୍ ଜ୍ୟାମିତିର ଏକ ଥିଓରେମ୍ ଯାହା ଡାରବକ୍ସଙ୍କ ଥିଓରେମ୍ କୁ ସାଧାରଣ କରିଥାଏ |
କାରାଥୋଡୋରୀର ବିସ୍ତାର ତତ୍ତ୍ୱ: ମାପ ତତ୍ତ୍ୱ ରେ, Carathéodory ର ବିସ୍ତୃତକରଣ theorem ରାଜ୍ୟ ଯେ R ଦ୍ଵାରା ଆୟୋଜିତ σ-algebra ଉପରେ ଏକ ମାପ ପାଇଁ କୌଣସି ପୂର୍ବରୁ ମାପ ଏକ ପ୍ରଦତ୍ତ ସେଟ୍ Ω ଉପସେଟ ଏକ ପ୍ରଦତ୍ତ ମୁଦି R ଉପରେ ବ୍ୟାଖ୍ୟା ଅନୁଲମ୍ବିତ କରାଯାଇପାରିବ, ଏବଂ ଏହି ବିସ୍ତୃତକରଣ ଯଦି pre- ଅନନ୍ୟ ଅଟେ ମାପ ହେଉଛି σ- ସୀମିତ | ଫଳସ୍ୱରୂପ, ପ୍ରକୃତ ସଂଖ୍ୟାଗୁଡ଼ିକର ସମସ୍ତ ବ୍ୟବଧାନ ଧାରଣ କରିଥିବା ଏକ ରିଙ୍ଗ ଉପରେ ଯେକ any ଣସି ପୂର୍ବ-ମାପ ପ୍ରକୃତ ସଂଖ୍ୟା ସେଟ୍ ର ବୋରେଲ୍ ବୀଜ ବର୍ଣ୍ଣିତକୁ ବିସ୍ତାର କରାଯାଇପାରେ | ମାପ ସିଦ୍ଧାନ୍ତର ଏହା ଏକ ଅତ୍ୟନ୍ତ ଶକ୍ତିଶାଳୀ ଫଳାଫଳ, ଏବଂ ଉଦାହରଣ ସ୍ୱରୂପ, ଲେବେସଗୁ ମାପକୁ ନେଇଥାଏ |
କାରାଥିସ୍: କାରାଥିସ୍ ଏରେବିଡା ପରିବାରରେ ପୋକର ଏକ ବଂଶ | ୧ 666666 ମସିହାରେ ଅଗଷ୍ଟସ୍ ରେଡକଲିଫ୍ ଗ୍ରୋଟ୍ ଦ୍ୱାରା ଏହି ବଂଶ ବର୍ଣ୍ଣନା କରାଯାଇଥିଲା |
କାରାଥିସ୍ ଆଲାୟୋରମ୍: କାରାଟିସ୍ ଆଲାୟୋରମ୍ ହେଉଛି ଏରେବିଡା ପରିବାରର ଏକ ପୋକ ଯାହା ପ୍ରଥମେ 2011 ରେ ଭିଟର୍ ଓସମାର ବେକର୍ ଦ୍ୱାରା ବର୍ଣ୍ଣନା କରାଯାଇଥିଲା | ଏହା କ୍ୟୁବାରେ ମିଳିଥାଏ |
Carathis australis: 1909 ମସିହାରେ ୱାଲ୍ଟର ରୋଥଚିଲ୍ଡଙ୍କ ଦ୍ described ାରା ପ୍ରଥମେ ବର୍ଣ୍ଣିତ ଏରେବିଡା ପରିବାରର ଏକ ପୋକ ଅଟେ | ଏହା ବ୍ରାଜିଲରେ ମିଳିଥାଏ |
କାରାଟିସ୍ ବାଇବ୍ଲିସ୍: କାରାଥିସ୍ ବାଇବ୍ଲିସ୍ ହେଉଛି ଏରେବିଡା ପରିବାରର ଏକ ପୋକ ଯାହାକି ପ୍ରଥମେ ୧ 9292 ୨ ମସିହାରେ ୱିଲିୟମ୍ ସ୍କସ୍ ଦ୍ୱାରା ବର୍ଣ୍ଣନା କରାଯାଇଥିଲା | ଏହା ବ୍ରାଜିଲ, କୋଷ୍ଟାରିକା ଏବଂ ଗୁଆଟେମାଲାରେ ମିଳିଥାଏ |
କାରାଥିସ୍ ଗର୍ଟିନୋଏଡସ୍: 1866 ମସିହାରେ ଅଗଷ୍ଟସ୍ ରେଡକଲିଫ୍ ଗ୍ରୋଟ୍ ଦ୍ୱାରା ବର୍ଣ୍ଣିତ ଏରେବିଡା ପରିବାରର ଏକ ପୋକ ଅଟେ | ଏହା କ୍ୟୁବାରେ ମିଳିଥାଏ |
ଟେସେଲା କ୍ଲାଗେସି: ଟେସେଲା କ୍ଲାଗେସି ଏରେବିଡା ପରିବାରର ଏକ ପୋକ ଅଟେ | ଏହାକୁ ୱାଲ୍ଟର ରୋଥଚିଲ୍ଡ 1909 ରେ ବର୍ଣ୍ଣନା କରିଥିଲେ। ଏହା ବ୍ରାଜିଲ, ଫ୍ରେଞ୍ଚ ଗୁଇନା ଏବଂ ଇକ୍ୟୁଏଡରରେ ଦେଖିବାକୁ ମିଳେ।
କାରାଟିସ୍ ବାଇବ୍ଲିସ୍: କାରାଥିସ୍ ବାଇବ୍ଲିସ୍ ହେଉଛି ଏରେବିଡା ପରିବାରର ଏକ ପୋକ ଯାହାକି ପ୍ରଥମେ ୧ 9292 ୨ ମସିହାରେ ୱିଲିୟମ୍ ସ୍କସ୍ ଦ୍ୱାରା ବର୍ଣ୍ଣନା କରାଯାଇଥିଲା | ଏହା ବ୍ରାଜିଲ, କୋଷ୍ଟାରିକା ଏବଂ ଗୁଆଟେମାଲାରେ ମିଳିଥାଏ |
ଆମିଲିଆ ଓକେଣ୍ଡେନି: 1909 ମସିହାରେ ୱାଲ୍ଟର ରୋଥଚିଲ୍ଡଙ୍କ ଦ୍ୱାରା ବର୍ଣ୍ଣିତ ଏରେବିଡା ପରିବାରର ଏକ ପୋକ ଅଟେ। ଏହା ପେରୁ ଏବଂ ବୋଲିଭିଆରେ ମିଳିଥାଏ |
କାରାଥିସ୍ ପାଲପାଲିସ୍: କାରାଥିସ୍ ପାଲପାଲିସ୍ ହେଉଛି ଏରେବିଡା ପରିବାରର ଏକ ପୋକ ଯାହା ପ୍ରଥମେ ୧ 555555 ମସିହାରେ ଫ୍ରାନ୍ସିସ୍ ୱାକର୍ ଦ୍ୱାରା ବର୍ଣ୍ଣନା କରାଯାଇଥିଲା | ଏହା ଜାମାଇକାରେ ମିଳିଥାଏ |
ଆମିଲିଆ ପେରୋପାକା: ଆମିଲିଆ ପେରୋପାକା ଏରେବିଡା ପରିବାରର ଏକ ପୋକ ଅଟେ | 1920 ରେ ସେଇଜ୍ ଏହାକୁ ବର୍ଣ୍ଣନା କରିଥିଲେ | ଏହା କଲମ୍ବିଆରେ ମିଳିଥାଏ |
କାରାଟିସ୍ ସେପ୍ଟେଣ୍ଟ୍ରିଆନାଲିସ୍: କାରାଟିସ୍ ସେପ୍ଟେଣ୍ଟ୍ରିଆନାଲିସ୍ ହେଉଛି ଏରେବିଡା ପରିବାରର ଏକ ପୋକ ଯାହା ପ୍ରଥମେ 2011 ରେ ଭିଟର୍ ଓସମାର୍ ବେକର୍ ଦ୍ୱାରା ବର୍ଣ୍ଣନା କରାଯାଇଥିଲା | ଏହା କୋଷ୍ଟାରିକାରେ ମିଳିଥାଏ |
ଆମିଲିଆ ଟ୍ୟାବାକୋନାସ୍: ଆମିଲିଆ ଟ୍ୟାବାକୋନାସ୍ ଏରେବିଡା ପରିବାରର ଏକ ପୋକ ଅଟେ | ଏହାକୁ 1916 ମସିହାରେ ଜେମ୍ସ ଜନ୍ ଜୋସି ଏବଂ ଜର୍ଜ ତାଲବଟ୍ ବର୍ଣ୍ଣନା କରିଥିଲେ। ଏହା ପେରୁରେ ମିଳିଥାଏ |
କାରାଥ୍ରିପ୍ସ: କାରାଥ୍ରିପ୍ସ ଫ୍ଲେଓଥ୍ରିପିଡା ପରିବାରର ଥ୍ରିପ୍ସର ଏକ ବଂଶ |
କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀ: କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀ ଜଣେ ଗ୍ରୀକ୍ ଗଣିତଜ୍ଞ ଥିଲେ ଯିଏକି ତାଙ୍କର ବୃତ୍ତିଗତ ବୃତ୍ତିର ଅଧିକାଂଶ ସମୟ ଜର୍ମାନୀରେ ବିତାଇଥିଲେ | ବାସ୍ତବ ଏବଂ ଜଟିଳ ବିଶ୍ଳେଷଣ, ଭିନ୍ନତାର ଗଣନା, ଏବଂ ମାପ ସିଦ୍ଧାନ୍ତରେ ସେ ମହତ୍ contributions ପୂର୍ଣ ଅବଦାନ ରଖିଥିଲେ | ସେ ଥର୍ମୋଡାଇନାମିକ୍ସର ଏକ ସ୍ୱୀକୃତିପ୍ରାପ୍ତ ସୂତ୍ର ମଧ୍ୟ ସୃଷ୍ଟି କରିଥିଲେ |
କାରାଥୋଡୋରିର ମାନଦଣ୍ଡ: କାରାଥୋଡୋରୀର ମାନଦଣ୍ଡ ହେଉଛି ମାପ ସିଦ୍ଧାନ୍ତର ଏକ ଫଳାଫଳ ଯାହା ଗ୍ରୀକ୍ ଗଣିତଜ୍ଞ କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀ ଦ୍ୱାରା ପ୍ରସ୍ତୁତ କରାଯାଇଥିଲା | ଏହାର ଷ୍ଟେଟମେଣ୍ଟ ନିମ୍ନରେ ଦିଆଯାଇଛି: ଚାଲ | ଲେବସ୍ଗେ ବାହ୍ୟ ମାପକୁ ସୂଚିତ କରେ | , ଏବଂ ଦିଅନ୍ତୁ | । ତା'ପରେ ଯଦି ଏବଂ କେବଳ ଯଦି ଲେବେସଗୁ ମାପଯୋଗ୍ୟ | ପ୍ରତ୍ୟେକଙ୍କ ପାଇଁ , ର ସପ୍ଲିମେଣ୍ଟକୁ ଦର୍ଶାଉଛି | ଧ୍ୟାନ ଦିଅନ୍ତୁ | ଏକ ମାପଯୋଗ୍ୟ ସେଟ୍ ହେବା ଆବଶ୍ୟକ ନୁହେଁ |
କାରାଥୋଡୋରିର ଅସ୍ତିତ୍ୱ ଥିଓରେମ୍: ଗଣିତରେ, କାରାଥୋଡୋରିର ଅସ୍ତିତ୍ୱ ଥିଓରେମ୍ କହିଛି ଯେ ସାମାନ୍ୟ ଭିନ୍ନ ଅବସ୍ଥାରେ ଏକ ସାଧାରଣ ଡିଫେରିଏଲ୍ ସମୀକରଣର ସମାଧାନ ଅଛି | ଏହା Peano ର ଅସ୍ତିତ୍ୱ ଥିଓରେମର ଏକ ସାଧାରଣକରଣ | ପିଆନୋଙ୍କ ଥିଓରେମ୍ ଆବଶ୍ୟକ କରେ ଯେ ଡିଫେରିଏଲ୍ ସମୀକରଣର ଡାହାଣ ପାର୍ଶ୍ୱ ନିରନ୍ତର ରହିବା ଆବଶ୍ୟକ, ଯେତେବେଳେ କି କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ କିଛି ବିଚ୍ଛିନ୍ନ ସମୀକରଣ ପାଇଁ ସମାଧାନର ଅସ୍ତିତ୍ୱ ଦେଖାଏ | ଥିଓରେମ୍ କନଷ୍ଟାଣ୍ଟିନ୍ କାରାଥୋଡୋରୀଙ୍କ ନାମରେ ନାମିତ |
କାରାଥୋଡୋରୀର ବିସ୍ତାର ତତ୍ତ୍ୱ: ମାପ ତତ୍ତ୍ୱ ରେ, Carathéodory ର ବିସ୍ତୃତକରଣ theorem ରାଜ୍ୟ ଯେ R ଦ୍ଵାରା ଆୟୋଜିତ σ-algebra ଉପରେ ଏକ ମାପ ପାଇଁ କୌଣସି ପୂର୍ବରୁ ମାପ ଏକ ପ୍ରଦତ୍ତ ସେଟ୍ Ω ଉପସେଟ ଏକ ପ୍ରଦତ୍ତ ମୁଦି R ଉପରେ ବ୍ୟାଖ୍ୟା ଅନୁଲମ୍ବିତ କରାଯାଇପାରିବ, ଏବଂ ଏହି ବିସ୍ତୃତକରଣ ଯଦି pre- ଅନନ୍ୟ ଅଟେ ମାପ ହେଉଛି σ- ସୀମିତ | ଫଳସ୍ୱରୂପ, ପ୍ରକୃତ ସଂଖ୍ୟାଗୁଡ଼ିକର ସମସ୍ତ ବ୍ୟବଧାନ ଧାରଣ କରିଥିବା ଏକ ରିଙ୍ଗ ଉପରେ ଯେକ any ଣସି ପୂର୍ବ-ମାପ ପ୍ରକୃତ ସଂଖ୍ୟା ସେଟ୍ ର ବୋରେଲ୍ ବୀଜ ବର୍ଣ୍ଣିତକୁ ବିସ୍ତାର କରାଯାଇପାରେ | ମାପ ସିଦ୍ଧାନ୍ତର ଏହା ଏକ ଅତ୍ୟନ୍ତ ଶକ୍ତିଶାଳୀ ଫଳାଫଳ, ଏବଂ ଉଦାହରଣ ସ୍ୱରୂପ, ଲେବେସଗୁ ମାପକୁ ନେଇଥାଏ |
କାରାଥୋଡୋରୀ କର୍ଣ୍ଣଲ ଥିଓରେମ୍: ଗଣିତରେ, 1912 ମସିହାରେ ଗ୍ରୀକ୍ ଗଣିତଜ୍ଞ କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀଙ୍କ ଦ୍ established ାରା ସ୍ଥାପିତ ଜଟିଳ ବିଶ୍ଳେଷଣ ଏବଂ ଜ୍ୟାମିତିକ ଫଙ୍କସନ୍ ସିଦ୍ଧାନ୍ତରେ କାରାଥୋଡୋରୀ କର୍ଣ୍ଣଲ ଥିଓରେମ୍ ହେଉଛି ଏକ ଫଳାଫଳ | ଏବଂ ଫିକ୍ସିଂ 0, କାର୍ଯ୍ୟଗୁଡ଼ିକର ପ୍ରତିଛବିଗୁଡ଼ିକର ସୀମିତ ଆଚରଣ ଦୃଷ୍ଟିରୁ ଜ୍ୟାମିତିକ ଭାବରେ ନିର୍ଦ୍ଧିଷ୍ଟ ହୋଇପାରିବ | ଅସମାନ କାର୍ଯ୍ୟଗୁଡ଼ିକର ସିଦ୍ଧାନ୍ତରେ କର୍ଣ୍ଣଲ ଥିଓରେମର ବ୍ୟାପକ ପ୍ରୟୋଗ ରହିଛି ଏବଂ ବିଶେଷ ଭାବରେ ଲୋଏନର୍ ଡିଫେରିଏଲ୍ ସମୀକରଣ ପାଇଁ ଜ୍ୟାମିତିକ ଆଧାର ପ୍ରଦାନ କରିଥାଏ |
ନେଭାନଲିନାଙ୍କ ମାନଦଣ୍ଡ: ଗଣିତରେ, ଜଟିଳ ବିଶ୍ଳେଷଣରେ ନେଭାନଲିନାଙ୍କ ମାନଦଣ୍ଡ , 1920 ରେ ଫିନଲ୍ୟାଣ୍ଡର ଗଣିତଜ୍ଞ ରୋଲଫ ନେଭାନଲିନାଙ୍କ ଦ୍ proved ାରା ପ୍ରମାଣିତ ହୋଇଥିଲା, ୟୁନିଟ୍ ଡିସ୍କରେ ହୋଲୋମୋର୍ଫିକ୍ ଅସମାନ କାର୍ଯ୍ୟଗୁଡ଼ିକୁ ବର୍ଣ୍ଣିତ କରେ ଯାହା ତାରା ଭଳି | ଷ୍ଟାର ପରି ଅସମାନ କାର୍ଯ୍ୟଗୁଡ଼ିକ ପାଇଁ ବିବର୍ବାକ୍ ଧାରଣାକୁ ପ୍ରମାଣ କରିବାକୁ ନେଭାନ୍ଲିନା ଏହି ମାନଦଣ୍ଡ ବ୍ୟବହାର କରିଥିଲେ |
ବାହ୍ୟ ମାପ: ମାପ ତତ୍ତ୍ of ର ଗାଣିତିକ କ୍ଷେତ୍ରରେ, ଏକ ବାହ୍ୟ ମାପ ବା ବାହ୍ୟ ମାପ ହେଉଛି ଏକ କାର୍ଯ୍ୟ ଯାହାକି ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ସେଟ୍ ର ସମସ୍ତ ସବ୍ସେଟରେ ବ୍ୟାଖ୍ୟା କରାଯାଇଥାଏ ଯାହାକି ବର୍ଦ୍ଧିତ ପ୍ରକୃତ ସଂଖ୍ୟାରେ ମୂଲ୍ୟ ସହିତ କିଛି ଅତିରିକ୍ତ ବ technical ଷୟିକ ଅବସ୍ଥା ପୂରଣ କରେ | ମାପ କରାଯାଉଥିବା ସେଟ୍ ଏବଂ ଗଣନାତ୍ମକ ଭାବରେ ଯୋଗୀ ପଦକ୍ଷେପଗୁଡ଼ିକର ତତ୍ତ୍ for ପାଇଁ ଏକ ଅବଷ୍ଟ୍ରାକ୍ଟ ଆଧାର ଯୋଗାଇବା ପାଇଁ ପ୍ରଥମେ କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀ ଦ୍ୱାରା ବାହ୍ୟ ପଦକ୍ଷେପଗୁଡ଼ିକର ସିଦ୍ଧାନ୍ତ ପ୍ରବର୍ତ୍ତିତ ହୋଇଥିଲା | ବାହ୍ୟ ପଦକ୍ଷେପ ଉପରେ କାରାଥୋଡୋରିଙ୍କ କାର୍ଯ୍ୟ ମାପ-ଥିଓରେଟିକ୍ ସେଟ୍ ସିଦ୍ଧାନ୍ତରେ ଅନେକ ପ୍ରୟୋଗ ପାଇଲା, ଏବଂ ହାଉସଡର୍ଫ ଦ୍ by ାରା ଏକ ଡାଇମେନ୍ସନ୍ ପରି ମେଟ୍ରିକ୍ ଇନଭାରିଅଣ୍ଟକୁ ବର୍ତ୍ତମାନ ହାଉସଡର୍ଫ୍ ଡାଇମେନ୍ସନ୍ ଭାବରେ ବ୍ୟାଖ୍ୟା କରିବାକୁ ଏକ ଜରୁରୀ ଉପାୟରେ ବ୍ୟବହୃତ ହୋଇଥିଲା | ଜ୍ୟାମିତିକ ମାପ ସିଦ୍ଧାନ୍ତ କ୍ଷେତ୍ରରେ ବାହ୍ୟ ମାପ ସାଧାରଣତ used ବ୍ୟବହୃତ ହୁଏ |
କାରାଥୋଡୋରୀଙ୍କ ଥିଓରେମ୍: ଗଣିତରେ, କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀର ଅନେକ ଫଳାଫଳ ମଧ୍ୟରୁ ଗୋଟିଏକୁ ସୂଚାଇପାରେ: ସୀମା ପର୍ଯ୍ୟନ୍ତ କନଫର୍ମାଲ୍ ମ୍ୟାପିଂର ବିସ୍ତାର ବିଷୟରେ କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ | ଇଉକ୍ଲିଡିଆନ୍ ସ୍ପେସରେ ସେଟ୍ ର କନଭକ୍ସ ହଲ୍ ବିଷୟରେ କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ | ସାଧାରଣ ଡିଫେରିଏଲ୍ ସମୀକରଣର ସମାଧାନର ଅସ୍ତିତ୍ about ବିଷୟରେ କାରାଥୋଡୋରୀର ଅସ୍ତିତ୍ୱ ଥିଓରେମ୍ | ଏକ ମାପର ବିସ୍ତାର ବିଷୟରେ କାରାଥୋଡୋରୀର ବିସ୍ତାର ତତ୍ତ୍। | ଏକ ଜଟିଳ ଆନାଲିଟିକ୍ କାର୍ଯ୍ୟର ସୀମା ବିଷୟରେ ବୋରେଲ୍ - କାରାଥୋଡୋରୀ ଥିଓରେମ୍ | କାରାଥୋଡୋରୀ - ଜାକୋବି - ମିଛ ଥିଓରେମ୍, ସିମ୍ପ୍ଲେକ୍ଟିକ୍ ଟପୋଲୋଜିରେ ଡାରବକ୍ସଙ୍କ ଥିଓରେମର ଏକ ସାଧାରଣକରଣ | କାରାଥୋଡୋରୀର ମାନଦଣ୍ଡ, ଏକ ମାପଯୋଗ୍ୟ ସେଟ୍ ପାଇଁ ଏକ ଆବଶ୍ୟକୀୟ ଏବଂ ପର୍ଯ୍ୟାପ୍ତ ସର୍ତ୍ତ | କାରାଥୋଡୋରୀ କର୍ଣ୍ଣଲ ଥିଓରେମ୍, ଅସମାନ କାର୍ଯ୍ୟଗୁଡ଼ିକର ସ୍ଥାନୀୟ ୟୁନିଫର୍ମ ସମ୍ମିଶ୍ରଣ ପାଇଁ ଏକ ଜ୍ୟାମିତିକ ମାନଦଣ୍ଡ |
କାରାଥୋଡୋରିର ଥିଓରେମ୍ (କନଫର୍ମାଲ୍ ମ୍ୟାପିଙ୍ଗ୍): ଗଣିତରେ, କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ ହେଉଛି ଜଟିଳ ବିଶ୍ଳେଷଣରେ ଏକ ଥିଓରେମ୍, କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀଙ୍କ ନାମରେ ନାମିତ, ଯାହା ରିମାନ୍ ମ୍ୟାପିଙ୍ଗ୍ ଥିଓରେମ୍ ବିସ୍ତାର କରେ | 1913 ରେ ପ୍ରଥମେ ପ୍ରମାଣିତ ହୋଇଥିବା ଥିଓରେମ୍ରେ ଦର୍ଶାଯାଇଛି ଯେ ଜୋର୍ଡାନ ବକ୍ର ଦ୍ୱାରା ସୀମିତ ଜଟିଳ ବିମାନରେ ୟୁନିଟ୍ ଡିସ୍କକୁ ପଠାଉଥିବା କନଫର୍ମାଲ୍ ମ୍ୟାପିଙ୍ଗ୍ କ୍ରମାଗତ ଭାବରେ ୟୁନିଟ୍ ସର୍କଲରୁ ଜୋର୍ଡାନ ବକ୍ର ପର୍ଯ୍ୟନ୍ତ ଏକ ହୋମିଓମୋର୍ଫିଜିମ୍ ପର୍ଯ୍ୟନ୍ତ ବିସ୍ତାର କରିଥାଏ | ଫଳାଫଳ ହେଉଛି ପ୍ରଧାନ ଶେଷରେ କାରାଥୋଡୋରୀର ଫଳାଫଳ ଏବଂ ଅସମାନ ହୋଲୋମୋର୍ଫିକ୍ କାର୍ଯ୍ୟଗୁଡ଼ିକର ସୀମା ଆଚରଣ |
କାରାଥୋଡୋରିର ଥିଓରେମ୍ (କନଭକ୍ସ ହଲ୍): କାରାଥେଡୋରିର ଥିଓରେମ୍ ହେଉଛି କନଭକ୍ସ ଜ୍ୟାମିତିର ଏକ ଥିଓରେମ୍ | ଏହା ହେଉଛି ସବୁଠାରୁ d + 1 ଯଥା ପି ରେ ପଦକ୍ଷେପରେ ଏକ ସେଟ୍ P ର convex Hull ରେ R d ମିଥ୍ଯା ର ଏକ ବିନ୍ଦୁ x, ତେବେ x ର convex ସମଷ୍ଟି ଭାବରେ ଲେଖାଯାଇପାରିବ ଯଦି େସଠାେର ଅଛନ୍ତି P ଏକ ଉପସେଟ୍ P 'ଗଠିତ ଆମେରିକାନ୍ d + 1 କିମ୍ବା କମ୍ ପଏଣ୍ଟଗୁଡିକ ଯେପରିକି x P ର କନଭକ୍ସ ହଲ୍ ରେ ଅଛି | ସମାନ ଭାବରେ, x ଏକ R- ସିମ୍ପ୍ଲେକ୍ସରେ P ରେ ଥିବା ଭର୍ଟିକ୍ସ ସହିତ ଅଛି, ଯେଉଁଠାରେ | । କ୍ଷୁଦ୍ର r ଯାହାକି P ର କନଭକ୍ସ ହଲ୍ ରେ ପ୍ରତ୍ୟେକ x ପାଇଁ ଶେଷ ଷ୍ଟେଟମେଣ୍ଟକୁ ବ valid ଧ କରେ , କାରାଥୋଡୋରୀର P ସଂଖ୍ୟା ଭାବରେ ବ୍ୟାଖ୍ୟା କରାଯାଇଛି | P ର ଗୁଣ ଉପରେ ନିର୍ଭର କରି, କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ ଦ୍ୱାରା ପ୍ରଦତ୍ତ ସୀମାଠାରୁ କମ୍ ଉପର ସୀମା ମିଳିପାରିବ | ଧ୍ୟାନ ଦିଅନ୍ତୁ ଯେ P ନିଜେ କନଭକ୍ସ ହେବା ଆବଶ୍ୟକ ନୁହେଁ | ଏହା ଏକ ପରିଣାମ ଯେ P 'ସର୍ବଦା ହୋଇପାରେ P ରେ extremal, ଭାବରେ ଅଣ-extremal ବିନ୍ଦୁ convex Hull ରେ X ର ସଦସ୍ୟତା ପରିବର୍ତ୍ତନ ନକରି P ଅପସାରିତ ହୋଇପାରିବ ହେଉଛି।
କାରାଥୋଡୋରୀଙ୍କ ଥିଓରେମ୍: ଗଣିତରେ, କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀର ଅନେକ ଫଳାଫଳ ମଧ୍ୟରୁ ଗୋଟିଏକୁ ସୂଚାଇପାରେ: ସୀମା ପର୍ଯ୍ୟନ୍ତ କନଫର୍ମାଲ୍ ମ୍ୟାପିଂର ବିସ୍ତାର ବିଷୟରେ କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ | ଇଉକ୍ଲିଡିଆନ୍ ସ୍ପେସରେ ସେଟ୍ ର କନଭକ୍ସ ହଲ୍ ବିଷୟରେ କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ | ସାଧାରଣ ଡିଫେରିଏଲ୍ ସମୀକରଣର ସମାଧାନର ଅସ୍ତିତ୍ about ବିଷୟରେ କାରାଥୋଡୋରୀର ଅସ୍ତିତ୍ୱ ଥିଓରେମ୍ | ଏକ ମାପର ବିସ୍ତାର ବିଷୟରେ କାରାଥୋଡୋରୀର ବିସ୍ତାର ତତ୍ତ୍। | ଏକ ଜଟିଳ ଆନାଲିଟିକ୍ କାର୍ଯ୍ୟର ସୀମା ବିଷୟରେ ବୋରେଲ୍ - କାରାଥୋଡୋରୀ ଥିଓରେମ୍ | କାରାଥୋଡୋରୀ - ଜାକୋବି - ମିଛ ଥିଓରେମ୍, ସିମ୍ପ୍ଲେକ୍ଟିକ୍ ଟପୋଲୋଜିରେ ଡାରବକ୍ସଙ୍କ ଥିଓରେମର ଏକ ସାଧାରଣକରଣ | କାରାଥୋଡୋରୀର ମାନଦଣ୍ଡ, ଏକ ମାପଯୋଗ୍ୟ ସେଟ୍ ପାଇଁ ଏକ ଆବଶ୍ୟକୀୟ ଏବଂ ପର୍ଯ୍ୟାପ୍ତ ସର୍ତ୍ତ | କାରାଥୋଡୋରୀ କର୍ଣ୍ଣଲ ଥିଓରେମ୍, ଅସମାନ କାର୍ଯ୍ୟଗୁଡ଼ିକର ସ୍ଥାନୀୟ ୟୁନିଫର୍ମ ସମ୍ମିଶ୍ରଣ ପାଇଁ ଏକ ଜ୍ୟାମିତିକ ମାନଦଣ୍ଡ |
ବାହ୍ୟ ମାପ: ମାପ ତତ୍ତ୍ of ର ଗାଣିତିକ କ୍ଷେତ୍ରରେ, ଏକ ବାହ୍ୟ ମାପ ବା ବାହ୍ୟ ମାପ ହେଉଛି ଏକ କାର୍ଯ୍ୟ ଯାହାକି ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ସେଟ୍ ର ସମସ୍ତ ସବ୍ସେଟରେ ବ୍ୟାଖ୍ୟା କରାଯାଇଥାଏ ଯାହାକି ବର୍ଦ୍ଧିତ ପ୍ରକୃତ ସଂଖ୍ୟାରେ ମୂଲ୍ୟ ସହିତ କିଛି ଅତିରିକ୍ତ ବ technical ଷୟିକ ଅବସ୍ଥା ପୂରଣ କରେ | ମାପ କରାଯାଉଥିବା ସେଟ୍ ଏବଂ ଗଣନାତ୍ମକ ଭାବରେ ଯୋଗୀ ପଦକ୍ଷେପଗୁଡ଼ିକର ତତ୍ତ୍ for ପାଇଁ ଏକ ଅବଷ୍ଟ୍ରାକ୍ଟ ଆଧାର ଯୋଗାଇବା ପାଇଁ ପ୍ରଥମେ କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀ ଦ୍ୱାରା ବାହ୍ୟ ପଦକ୍ଷେପଗୁଡ଼ିକର ସିଦ୍ଧାନ୍ତ ପ୍ରବର୍ତ୍ତିତ ହୋଇଥିଲା | ବାହ୍ୟ ପଦକ୍ଷେପ ଉପରେ କାରାଥୋଡୋରିଙ୍କ କାର୍ଯ୍ୟ ମାପ-ଥିଓରେଟିକ୍ ସେଟ୍ ସିଦ୍ଧାନ୍ତରେ ଅନେକ ପ୍ରୟୋଗ ପାଇଲା, ଏବଂ ହାଉସଡର୍ଫ ଦ୍ by ାରା ଏକ ଡାଇମେନ୍ସନ୍ ପରି ମେଟ୍ରିକ୍ ଇନଭାରିଅଣ୍ଟକୁ ବର୍ତ୍ତମାନ ହାଉସଡର୍ଫ୍ ଡାଇମେନ୍ସନ୍ ଭାବରେ ବ୍ୟାଖ୍ୟା କରିବାକୁ ଏକ ଜରୁରୀ ଉପାୟରେ ବ୍ୟବହୃତ ହୋଇଥିଲା | ଜ୍ୟାମିତିକ ମାପ ସିଦ୍ଧାନ୍ତ କ୍ଷେତ୍ରରେ ବାହ୍ୟ ମାପ ସାଧାରଣତ used ବ୍ୟବହୃତ ହୁଏ |
କାରାଥୋଡୋରୀ - ଜାକୋବି - ମିଥ୍ୟା ତତ୍ତ୍ୱ: କାରାଥୋଡୋରୀ - ଜାକୋବି - ମିଛ ଥିଓରେମ୍ ହେଉଛି ସିମ୍ପଲେକ୍ଟିକ୍ ଜ୍ୟାମିତିର ଏକ ଥିଓରେମ୍ ଯାହା ଡାରବକ୍ସଙ୍କ ଥିଓରେମ୍ କୁ ସାଧାରଣ କରିଥାଏ |
ବାହ୍ୟ ମାପ: ମାପ ତତ୍ତ୍ of ର ଗାଣିତିକ କ୍ଷେତ୍ରରେ, ଏକ ବାହ୍ୟ ମାପ ବା ବାହ୍ୟ ମାପ ହେଉଛି ଏକ କାର୍ଯ୍ୟ ଯାହାକି ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ସେଟ୍ ର ସମସ୍ତ ସବ୍ସେଟରେ ବ୍ୟାଖ୍ୟା କରାଯାଇଥାଏ ଯାହାକି ବର୍ଦ୍ଧିତ ପ୍ରକୃତ ସଂଖ୍ୟାରେ ମୂଲ୍ୟ ସହିତ କିଛି ଅତିରିକ୍ତ ବ technical ଷୟିକ ଅବସ୍ଥା ପୂରଣ କରେ | ମାପ କରାଯାଉଥିବା ସେଟ୍ ଏବଂ ଗଣନାତ୍ମକ ଭାବରେ ଯୋଗୀ ପଦକ୍ଷେପଗୁଡ଼ିକର ତତ୍ତ୍ for ପାଇଁ ଏକ ଅବଷ୍ଟ୍ରାକ୍ଟ ଆଧାର ଯୋଗାଇବା ପାଇଁ ପ୍ରଥମେ କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀ ଦ୍ୱାରା ବାହ୍ୟ ପଦକ୍ଷେପଗୁଡ଼ିକର ସିଦ୍ଧାନ୍ତ ପ୍ରବର୍ତ୍ତିତ ହୋଇଥିଲା | ବାହ୍ୟ ପଦକ୍ଷେପ ଉପରେ କାରାଥୋଡୋରିଙ୍କ କାର୍ଯ୍ୟ ମାପ-ଥିଓରେଟିକ୍ ସେଟ୍ ସିଦ୍ଧାନ୍ତରେ ଅନେକ ପ୍ରୟୋଗ ପାଇଲା, ଏବଂ ହାଉସଡର୍ଫ ଦ୍ by ାରା ଏକ ଡାଇମେନ୍ସନ୍ ପରି ମେଟ୍ରିକ୍ ଇନଭାରିଅଣ୍ଟକୁ ବର୍ତ୍ତମାନ ହାଉସଡର୍ଫ୍ ଡାଇମେନ୍ସନ୍ ଭାବରେ ବ୍ୟାଖ୍ୟା କରିବାକୁ ଏକ ଜରୁରୀ ଉପାୟରେ ବ୍ୟବହୃତ ହୋଇଥିଲା | ଜ୍ୟାମିତିକ ମାପ ସିଦ୍ଧାନ୍ତ କ୍ଷେତ୍ରରେ ବାହ୍ୟ ମାପ ସାଧାରଣତ used ବ୍ୟବହୃତ ହୁଏ |
କାରାଥୋଡୋରୀ ଧାରଣା: ଡିଫେରିଏଲ୍ ଜ୍ୟାମିତ୍ରୀରେ , କାରାଥୋଡୋରୀ ଧାରଣା ହେଉଛି ଏକ ଗାଣିତିକ ଧାରଣା ଯାହାକି 1924 ମସିହାରେ ବର୍ଲିନ୍ ଗଣିତ ସୋସାଇଟିର ଏକ ଅଧିବେଶନରେ ହାନ୍ସ ଲୁଡୱିଗ୍ ହେମ୍ବର୍ଗର୍ଙ୍କ ଦ୍ୱାରା କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀ ଦ୍ୱାରା ଦର୍ଶାଯାଇଥିଲା। ଏଥିରେ, ଜନ୍ ଏଡେନ୍ସର୍ ଲିଟିଲଉଡ୍ ଏକ ଗାଣିତିକ ଦାବିର ଉଦାହରଣ ଭାବରେ ଧାରଣା ଏବଂ ହାମବର୍ଗର ଅବଦାନ ବିଷୟରେ ଉଲ୍ଲେଖ କରିଛନ୍ତି ଯାହା କହିବା ସହଜ କିନ୍ତୁ ପ୍ରମାଣ କରିବା କଷ୍ଟକର | ବିମାନ ବକ୍ର ପାଇଁ ଫୋର୍ ଭର୍ଟେକ୍ସ ଥିଓରେମ୍ ସହିତ କନଜେକ୍ଟରର ଆନୁଷ୍ଠାନିକ ଅନୁରୂପରେ ଡିର୍କ ଷ୍ଟ୍ରିକ୍ ବର୍ଣ୍ଣନା କରିଛନ୍ତି | ଧାରଣାକୁ ଆଧୁନିକ ସନ୍ଦର୍ଭଗୁଡ଼ିକ ହେଉଛି ଶିଙ୍ଗ-ତୁଙ୍ଗ ୟାଙ୍କ ସମସ୍ୟା ତାଲିକା, ମାର୍ସେଲ ବର୍ଗର୍ଙ୍କ ପୁସ୍ତକ ଏବଂ ପୁସ୍ତକଗୁଡ଼ିକ |
କାରାଥୋଡୋରୀ ଧାରଣା: ଡିଫେରିଏଲ୍ ଜ୍ୟାମିତ୍ରୀରେ , କାରାଥୋଡୋରୀ ଧାରଣା ହେଉଛି ଏକ ଗାଣିତିକ ଧାରଣା ଯାହାକି 1924 ମସିହାରେ ବର୍ଲିନ୍ ଗଣିତ ସୋସାଇଟିର ଏକ ଅଧିବେଶନରେ ହାନ୍ସ ଲୁଡୱିଗ୍ ହେମ୍ବର୍ଗର୍ଙ୍କ ଦ୍ୱାରା କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀ ଦ୍ୱାରା ଦର୍ଶାଯାଇଥିଲା। ଏଥିରେ, ଜନ୍ ଏଡେନ୍ସର୍ ଲିଟିଲଉଡ୍ ଏକ ଗାଣିତିକ ଦାବିର ଉଦାହରଣ ଭାବରେ ଧାରଣା ଏବଂ ହାମବର୍ଗର ଅବଦାନ ବିଷୟରେ ଉଲ୍ଲେଖ କରିଛନ୍ତି ଯାହା କହିବା ସହଜ କିନ୍ତୁ ପ୍ରମାଣ କରିବା କଷ୍ଟକର | ବିମାନ ବକ୍ର ପାଇଁ ଫୋର୍ ଭର୍ଟେକ୍ସ ଥିଓରେମ୍ ସହିତ କନଜେକ୍ଟରର ଆନୁଷ୍ଠାନିକ ଅନୁରୂପରେ ଡିର୍କ ଷ୍ଟ୍ରିକ୍ ବର୍ଣ୍ଣନା କରିଛନ୍ତି | ଧାରଣାକୁ ଆଧୁନିକ ସନ୍ଦର୍ଭଗୁଡ଼ିକ ହେଉଛି ଶିଙ୍ଗ-ତୁଙ୍ଗ ୟାଙ୍କ ସମସ୍ୟା ତାଲିକା, ମାର୍ସେଲ ବର୍ଗର୍ଙ୍କ ପୁସ୍ତକ ଏବଂ ପୁସ୍ତକଗୁଡ଼ିକ |
କାରାଥୋଡୋରିର ଅସ୍ତିତ୍ୱ ଥିଓରେମ୍: ଗଣିତରେ, କାରାଥୋଡୋରିର ଅସ୍ତିତ୍ୱ ଥିଓରେମ୍ କହିଛି ଯେ ସାମାନ୍ୟ ଭିନ୍ନ ଅବସ୍ଥାରେ ଏକ ସାଧାରଣ ଡିଫେରିଏଲ୍ ସମୀକରଣର ସମାଧାନ ଅଛି | ଏହା Peano ର ଅସ୍ତିତ୍ୱ ଥିଓରେମର ଏକ ସାଧାରଣକରଣ | ପିଆନୋଙ୍କ ଥିଓରେମ୍ ଆବଶ୍ୟକ କରେ ଯେ ଡିଫେରିଏଲ୍ ସମୀକରଣର ଡାହାଣ ପାର୍ଶ୍ୱ ନିରନ୍ତର ରହିବା ଆବଶ୍ୟକ, ଯେତେବେଳେ କି କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ କିଛି ବିଚ୍ଛିନ୍ନ ସମୀକରଣ ପାଇଁ ସମାଧାନର ଅସ୍ତିତ୍ୱ ଦେଖାଏ | ଥିଓରେମ୍ କନଷ୍ଟାଣ୍ଟିନ୍ କାରାଥୋଡୋରୀଙ୍କ ନାମରେ ନାମିତ |
କାରାଥୋଡୋରୀର ବିସ୍ତାର ତତ୍ତ୍ୱ: ମାପ ତତ୍ତ୍ୱ ରେ, Carathéodory ର ବିସ୍ତୃତକରଣ theorem ରାଜ୍ୟ ଯେ R ଦ୍ଵାରା ଆୟୋଜିତ σ-algebra ଉପରେ ଏକ ମାପ ପାଇଁ କୌଣସି ପୂର୍ବରୁ ମାପ ଏକ ପ୍ରଦତ୍ତ ସେଟ୍ Ω ଉପସେଟ ଏକ ପ୍ରଦତ୍ତ ମୁଦି R ଉପରେ ବ୍ୟାଖ୍ୟା ଅନୁଲମ୍ବିତ କରାଯାଇପାରିବ, ଏବଂ ଏହି ବିସ୍ତୃତକରଣ ଯଦି pre- ଅନନ୍ୟ ଅଟେ ମାପ ହେଉଛି σ- ସୀମିତ | ଫଳସ୍ୱରୂପ, ପ୍ରକୃତ ସଂଖ୍ୟାଗୁଡ଼ିକର ସମସ୍ତ ବ୍ୟବଧାନ ଧାରଣ କରିଥିବା ଏକ ରିଙ୍ଗ ଉପରେ ଯେକ any ଣସି ପୂର୍ବ-ମାପ ପ୍ରକୃତ ସଂଖ୍ୟା ସେଟ୍ ର ବୋରେଲ୍ ବୀଜ ବର୍ଣ୍ଣିତକୁ ବିସ୍ତାର କରାଯାଇପାରେ | ମାପ ସିଦ୍ଧାନ୍ତର ଏହା ଏକ ଅତ୍ୟନ୍ତ ଶକ୍ତିଶାଳୀ ଫଳାଫଳ, ଏବଂ ଉଦାହରଣ ସ୍ୱରୂପ, ଲେବେସଗୁ ମାପକୁ ନେଇଥାଏ |
କାରାଥୋଡୋରୀ କର୍ଣ୍ଣଲ ଥିଓରେମ୍: ଗଣିତରେ, 1912 ମସିହାରେ ଗ୍ରୀକ୍ ଗଣିତଜ୍ଞ କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀଙ୍କ ଦ୍ established ାରା ସ୍ଥାପିତ ଜଟିଳ ବିଶ୍ଳେଷଣ ଏବଂ ଜ୍ୟାମିତିକ ଫଙ୍କସନ୍ ସିଦ୍ଧାନ୍ତରେ କାରାଥୋଡୋରୀ କର୍ଣ୍ଣଲ ଥିଓରେମ୍ ହେଉଛି ଏକ ଫଳାଫଳ | ଏବଂ ଫିକ୍ସିଂ 0, କାର୍ଯ୍ୟଗୁଡ଼ିକର ପ୍ରତିଛବିଗୁଡ଼ିକର ସୀମିତ ଆଚରଣ ଦୃଷ୍ଟିରୁ ଜ୍ୟାମିତିକ ଭାବରେ ନିର୍ଦ୍ଧିଷ୍ଟ ହୋଇପାରିବ | ଅସମାନ କାର୍ଯ୍ୟଗୁଡ଼ିକର ସିଦ୍ଧାନ୍ତରେ କର୍ଣ୍ଣଲ ଥିଓରେମର ବ୍ୟାପକ ପ୍ରୟୋଗ ରହିଛି ଏବଂ ବିଶେଷ ଭାବରେ ଲୋଏନର୍ ଡିଫେରିଏଲ୍ ସମୀକରଣ ପାଇଁ ଜ୍ୟାମିତିକ ଆଧାର ପ୍ରଦାନ କରିଥାଏ |
ବାହ୍ୟ ମାପ: ମାପ ତତ୍ତ୍ of ର ଗାଣିତିକ କ୍ଷେତ୍ରରେ, ଏକ ବାହ୍ୟ ମାପ ବା ବାହ୍ୟ ମାପ ହେଉଛି ଏକ କାର୍ଯ୍ୟ ଯାହାକି ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ସେଟ୍ ର ସମସ୍ତ ସବ୍ସେଟରେ ବ୍ୟାଖ୍ୟା କରାଯାଇଥାଏ ଯାହାକି ବର୍ଦ୍ଧିତ ପ୍ରକୃତ ସଂଖ୍ୟାରେ ମୂଲ୍ୟ ସହିତ କିଛି ଅତିରିକ୍ତ ବ technical ଷୟିକ ଅବସ୍ଥା ପୂରଣ କରେ | ମାପ କରାଯାଉଥିବା ସେଟ୍ ଏବଂ ଗଣନାତ୍ମକ ଭାବରେ ଯୋଗୀ ପଦକ୍ଷେପଗୁଡ଼ିକର ତତ୍ତ୍ for ପାଇଁ ଏକ ଅବଷ୍ଟ୍ରାକ୍ଟ ଆଧାର ଯୋଗାଇବା ପାଇଁ ପ୍ରଥମେ କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀ ଦ୍ୱାରା ବାହ୍ୟ ପଦକ୍ଷେପଗୁଡ଼ିକର ସିଦ୍ଧାନ୍ତ ପ୍ରବର୍ତ୍ତିତ ହୋଇଥିଲା | ବାହ୍ୟ ପଦକ୍ଷେପ ଉପରେ କାରାଥୋଡୋରିଙ୍କ କାର୍ଯ୍ୟ ମାପ-ଥିଓରେଟିକ୍ ସେଟ୍ ସିଦ୍ଧାନ୍ତରେ ଅନେକ ପ୍ରୟୋଗ ପାଇଲା, ଏବଂ ହାଉସଡର୍ଫ ଦ୍ by ାରା ଏକ ଡାଇମେନ୍ସନ୍ ପରି ମେଟ୍ରିକ୍ ଇନଭାରିଅଣ୍ଟକୁ ବର୍ତ୍ତମାନ ହାଉସଡର୍ଫ୍ ଡାଇମେନ୍ସନ୍ ଭାବରେ ବ୍ୟାଖ୍ୟା କରିବାକୁ ଏକ ଜରୁରୀ ଉପାୟରେ ବ୍ୟବହୃତ ହୋଇଥିଲା | ଜ୍ୟାମିତିକ ମାପ ସିଦ୍ଧାନ୍ତ କ୍ଷେତ୍ରରେ ବାହ୍ୟ ମାପ ସାଧାରଣତ used ବ୍ୟବହୃତ ହୁଏ |
କାରାଥୋଡୋରୀ ମେଟ୍ରିକ୍: ଗଣିତରେ, କାରାଥୋଡୋରୀ ମେଟ୍ରିକ୍ ହେଉଛି ଏକ ମେଟ୍ରିକ୍ ଯାହା ଏକ ଜଟିଳ ବନାଚ୍ ସ୍ପେସ୍ ର ଖୋଲା ୟୁନିଟ୍ ବଲ୍ ଉପରେ ବ୍ୟାଖ୍ୟା କରାଯାଇଛି ଯାହାର ହାଇପରବୋଲିକ୍ ଜ୍ୟାମିତିର ପୋଇନାର୍ ମେଟ୍ରିକ୍ ସହିତ ଅନେକ ସମାନ ଗୁଣ ଅଛି | ଗ୍ରୀକ୍ ଗଣିତଜ୍ଞ କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀଙ୍କ ନାମରେ ଏହାର ନାମକରଣ କରାଯାଇଛି |
କାରାଥୋଡୋରୀଙ୍କ ଥିଓରେମ୍: ଗଣିତରେ, କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀର ଅନେକ ଫଳାଫଳ ମଧ୍ୟରୁ ଗୋଟିଏକୁ ସୂଚାଇପାରେ: ସୀମା ପର୍ଯ୍ୟନ୍ତ କନଫର୍ମାଲ୍ ମ୍ୟାପିଂର ବିସ୍ତାର ବିଷୟରେ କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ | ଇଉକ୍ଲିଡିଆନ୍ ସ୍ପେସରେ ସେଟ୍ ର କନଭକ୍ସ ହଲ୍ ବିଷୟରେ କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ | ସାଧାରଣ ଡିଫେରିଏଲ୍ ସମୀକରଣର ସମାଧାନର ଅସ୍ତିତ୍ about ବିଷୟରେ କାରାଥୋଡୋରୀର ଅସ୍ତିତ୍ୱ ଥିଓରେମ୍ | ଏକ ମାପର ବିସ୍ତାର ବିଷୟରେ କାରାଥୋଡୋରୀର ବିସ୍ତାର ତତ୍ତ୍। | ଏକ ଜଟିଳ ଆନାଲିଟିକ୍ କାର୍ଯ୍ୟର ସୀମା ବିଷୟରେ ବୋରେଲ୍ - କାରାଥୋଡୋରୀ ଥିଓରେମ୍ | କାରାଥୋଡୋରୀ - ଜାକୋବି - ମିଛ ଥିଓରେମ୍, ସିମ୍ପ୍ଲେକ୍ଟିକ୍ ଟପୋଲୋଜିରେ ଡାରବକ୍ସଙ୍କ ଥିଓରେମର ଏକ ସାଧାରଣକରଣ | କାରାଥୋଡୋରୀର ମାନଦଣ୍ଡ, ଏକ ମାପଯୋଗ୍ୟ ସେଟ୍ ପାଇଁ ଏକ ଆବଶ୍ୟକୀୟ ଏବଂ ପର୍ଯ୍ୟାପ୍ତ ସର୍ତ୍ତ | କାରାଥୋଡୋରୀ କର୍ଣ୍ଣଲ ଥିଓରେମ୍, ଅସମାନ କାର୍ଯ୍ୟଗୁଡ଼ିକର ସ୍ଥାନୀୟ ୟୁନିଫର୍ମ ସମ୍ମିଶ୍ରଣ ପାଇଁ ଏକ ଜ୍ୟାମିତିକ ମାନଦଣ୍ଡ |
କାରାଥୋଡୋରିର ଥିଓରେମ୍ (କନଫର୍ମାଲ୍ ମ୍ୟାପିଙ୍ଗ୍): ଗଣିତରେ, କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ ହେଉଛି ଜଟିଳ ବିଶ୍ଳେଷଣରେ ଏକ ଥିଓରେମ୍, କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀଙ୍କ ନାମରେ ନାମିତ, ଯାହା ରିମାନ୍ ମ୍ୟାପିଙ୍ଗ୍ ଥିଓରେମ୍ ବିସ୍ତାର କରେ | 1913 ରେ ପ୍ରଥମେ ପ୍ରମାଣିତ ହୋଇଥିବା ଥିଓରେମ୍ରେ ଦର୍ଶାଯାଇଛି ଯେ ଜୋର୍ଡାନ ବକ୍ର ଦ୍ୱାରା ସୀମିତ ଜଟିଳ ବିମାନରେ ୟୁନିଟ୍ ଡିସ୍କକୁ ପଠାଉଥିବା କନଫର୍ମାଲ୍ ମ୍ୟାପିଙ୍ଗ୍ କ୍ରମାଗତ ଭାବରେ ୟୁନିଟ୍ ସର୍କଲରୁ ଜୋର୍ଡାନ ବକ୍ର ପର୍ଯ୍ୟନ୍ତ ଏକ ହୋମିଓମୋର୍ଫିଜିମ୍ ପର୍ଯ୍ୟନ୍ତ ବିସ୍ତାର କରିଥାଏ | ଫଳାଫଳ ହେଉଛି ପ୍ରଧାନ ଶେଷରେ କାରାଥୋଡୋରୀର ଫଳାଫଳ ଏବଂ ଅସମାନ ହୋଲୋମୋର୍ଫିକ୍ କାର୍ଯ୍ୟଗୁଡ଼ିକର ସୀମା ଆଚରଣ |
କାରାଥୋଡୋରିର ଥିଓରେମ୍ (କନଭକ୍ସ ହଲ୍): କାରାଥେଡୋରିର ଥିଓରେମ୍ ହେଉଛି କନଭକ୍ସ ଜ୍ୟାମିତିର ଏକ ଥିଓରେମ୍ | ଏହା ହେଉଛି ସବୁଠାରୁ d + 1 ଯଥା ପି ରେ ପଦକ୍ଷେପରେ ଏକ ସେଟ୍ P ର convex Hull ରେ R d ମିଥ୍ଯା ର ଏକ ବିନ୍ଦୁ x, ତେବେ x ର convex ସମଷ୍ଟି ଭାବରେ ଲେଖାଯାଇପାରିବ ଯଦି େସଠାେର ଅଛନ୍ତି P ଏକ ଉପସେଟ୍ P 'ଗଠିତ ଆମେରିକାନ୍ d + 1 କିମ୍ବା କମ୍ ପଏଣ୍ଟଗୁଡିକ ଯେପରିକି x P ର କନଭକ୍ସ ହଲ୍ ରେ ଅଛି | ସମାନ ଭାବରେ, x ଏକ R- ସିମ୍ପ୍ଲେକ୍ସରେ P ରେ ଥିବା ଭର୍ଟିକ୍ସ ସହିତ ଅଛି, ଯେଉଁଠାରେ | । କ୍ଷୁଦ୍ର r ଯାହାକି P ର କନଭକ୍ସ ହଲ୍ ରେ ପ୍ରତ୍ୟେକ x ପାଇଁ ଶେଷ ଷ୍ଟେଟମେଣ୍ଟକୁ ବ valid ଧ କରେ , କାରାଥୋଡୋରୀର P ସଂଖ୍ୟା ଭାବରେ ବ୍ୟାଖ୍ୟା କରାଯାଇଛି | P ର ଗୁଣ ଉପରେ ନିର୍ଭର କରି, କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ ଦ୍ୱାରା ପ୍ରଦତ୍ତ ସୀମାଠାରୁ କମ୍ ଉପର ସୀମା ମିଳିପାରିବ | ଧ୍ୟାନ ଦିଅନ୍ତୁ ଯେ P ନିଜେ କନଭକ୍ସ ହେବା ଆବଶ୍ୟକ ନୁହେଁ | ଏହା ଏକ ପରିଣାମ ଯେ P 'ସର୍ବଦା ହୋଇପାରେ P ରେ extremal, ଭାବରେ ଅଣ-extremal ବିନ୍ଦୁ convex Hull ରେ X ର ସଦସ୍ୟତା ପରିବର୍ତ୍ତନ ନକରି P ଅପସାରିତ ହୋଇପାରିବ ହେଉଛି।
କାରାଥୋଡୋରୀଙ୍କ ଥିଓରେମ୍: ଗଣିତରେ, କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀର ଅନେକ ଫଳାଫଳ ମଧ୍ୟରୁ ଗୋଟିଏକୁ ସୂଚାଇପାରେ: ସୀମା ପର୍ଯ୍ୟନ୍ତ କନଫର୍ମାଲ୍ ମ୍ୟାପିଂର ବିସ୍ତାର ବିଷୟରେ କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ | ଇଉକ୍ଲିଡିଆନ୍ ସ୍ପେସରେ ସେଟ୍ ର କନଭକ୍ସ ହଲ୍ ବିଷୟରେ କାରାଥୋଡୋରିଙ୍କ ଥିଓରେମ୍ | ସାଧାରଣ ଡିଫେରିଏଲ୍ ସମୀକରଣର ସମାଧାନର ଅସ୍ତିତ୍ about ବିଷୟରେ କାରାଥୋଡୋରୀର ଅସ୍ତିତ୍ୱ ଥିଓରେମ୍ | ଏକ ମାପର ବିସ୍ତାର ବିଷୟରେ କାରାଥୋଡୋରୀର ବିସ୍ତାର ତତ୍ତ୍। | ଏକ ଜଟିଳ ଆନାଲିଟିକ୍ କାର୍ଯ୍ୟର ସୀମା ବିଷୟରେ ବୋରେଲ୍ - କାରାଥୋଡୋରୀ ଥିଓରେମ୍ | କାରାଥୋଡୋରୀ - ଜାକୋବି - ମିଛ ଥିଓରେମ୍, ସିମ୍ପ୍ଲେକ୍ଟିକ୍ ଟପୋଲୋଜିରେ ଡାରବକ୍ସଙ୍କ ଥିଓରେମର ଏକ ସାଧାରଣକରଣ | କାରାଥୋଡୋରୀର ମାନଦଣ୍ଡ, ଏକ ମାପଯୋଗ୍ୟ ସେଟ୍ ପାଇଁ ଏକ ଆବଶ୍ୟକୀୟ ଏବଂ ପର୍ଯ୍ୟାପ୍ତ ସର୍ତ୍ତ | କାରାଥୋଡୋରୀ କର୍ଣ୍ଣଲ ଥିଓରେମ୍, ଅସମାନ କାର୍ଯ୍ୟଗୁଡ଼ିକର ସ୍ଥାନୀୟ ୟୁନିଫର୍ମ ସମ୍ମିଶ୍ରଣ ପାଇଁ ଏକ ଜ୍ୟାମିତିକ ମାନଦଣ୍ଡ |
ବାହ୍ୟ ମାପ: ମାପ ତତ୍ତ୍ of ର ଗାଣିତିକ କ୍ଷେତ୍ରରେ, ଏକ ବାହ୍ୟ ମାପ ବା ବାହ୍ୟ ମାପ ହେଉଛି ଏକ କାର୍ଯ୍ୟ ଯାହାକି ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ସେଟ୍ ର ସମସ୍ତ ସବ୍ସେଟରେ ବ୍ୟାଖ୍ୟା କରାଯାଇଥାଏ ଯାହାକି ବର୍ଦ୍ଧିତ ପ୍ରକୃତ ସଂଖ୍ୟାରେ ମୂଲ୍ୟ ସହିତ କିଛି ଅତିରିକ୍ତ ବ technical ଷୟିକ ଅବସ୍ଥା ପୂରଣ କରେ | ମାପ କରାଯାଉଥିବା ସେଟ୍ ଏବଂ ଗଣନାତ୍ମକ ଭାବରେ ଯୋଗୀ ପଦକ୍ଷେପଗୁଡ଼ିକର ତତ୍ତ୍ for ପାଇଁ ଏକ ଅବଷ୍ଟ୍ରାକ୍ଟ ଆଧାର ଯୋଗାଇବା ପାଇଁ ପ୍ରଥମେ କନଷ୍ଟାଣ୍ଟିନ କାରାଥୋଡୋରୀ ଦ୍ୱାରା ବାହ୍ୟ ପଦକ୍ଷେପଗୁଡ଼ିକର ସିଦ୍ଧାନ୍ତ ପ୍ରବର୍ତ୍ତିତ ହୋଇଥିଲା | ବାହ୍ୟ ପଦକ୍ଷେପ ଉପରେ କାରାଥୋଡୋରିଙ୍କ କାର୍ଯ୍ୟ ମାପ-ଥିଓରେଟିକ୍ ସେଟ୍ ସିଦ୍ଧାନ୍ତରେ ଅନେକ ପ୍ରୟୋଗ ପାଇଲା, ଏବଂ ହାଉସଡର୍ଫ ଦ୍ by ାରା ଏକ ଡାଇମେନ୍ସନ୍ ପରି ମେଟ୍ରିକ୍ ଇନଭାରିଅଣ୍ଟକୁ ବର୍ତ୍ତମାନ ହାଉସଡର୍ଫ୍ ଡାଇମେନ୍ସନ୍ ଭାବରେ ବ୍ୟାଖ୍ୟା କରିବାକୁ ଏକ ଜରୁରୀ ଉପାୟରେ ବ୍ୟବହୃତ ହୋଇଥିଲା | ଜ୍ୟାମିତିକ ମାପ ସିଦ୍ଧାନ୍ତ କ୍ଷେତ୍ରରେ ବାହ୍ୟ ମାପ ସାଧାରଣତ used ବ୍ୟବହୃତ ହୁଏ |
କାରାଥୋଡୋରୀ - ଜାକୋବି - ମିଥ୍ୟା ତତ୍ତ୍ୱ: କାରାଥୋଡୋରୀ - ଜାକୋବି - ମିଛ ଥିଓରେମ୍ ହେଉଛି ସିମ୍ପଲେକ୍ଟିକ୍ ଜ୍ୟାମିତିର ଏକ ଥିଓରେମ୍ ଯାହା ଡାରବକ୍ସଙ୍କ ଥିଓରେମ୍ କୁ ସାଧାରଣ କରିଥାଏ |
ସାଧାରଣ କାରୋଟିଡ୍ ଧମନୀ: ଶରୀର ବିଜ୍ଞାନ ରେ, ବାମ ଏବଂ ଡାହାଣ ସାଧାରଣ carotid arteries (carotids) arteries ମୁଣ୍ଡ ଏବଂ oxygenated ରକ୍ତ ସହିତ ବେକ ପ୍ରଦାନ ଯାହା ଅଛି; ସେମାନେ ବେକରେ ବିଭକ୍ତ ହୋଇ ବାହ୍ୟ ଏବଂ ଆଭ୍ୟନ୍ତରୀଣ କାରୋଟିଡ୍ ଧମନୀ ଗଠନ କରନ୍ତି |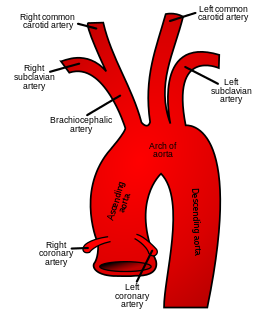
କାରାଟିଙ୍ଗା: କାରାଟିଙ୍ଗା ହେଉଛି ବ୍ରାଜିଲର ପୂର୍ବ ମିନାସ୍ ଜେରାଇସ୍ ରାଜ୍ୟର ଏକ ପ ity ରପାଳିକା | 2020 ରେ ଜନସଂଖ୍ୟା 92,603 ​​ବାସିନ୍ଦା ଏବଂ ପ municipal ରସଂସ୍ଥାର ମୋଟ କ୍ଷେତ୍ର ଥିଲା 1,251 କିମି 2 | ସମୁଦ୍ର ପତ୍ତନଠାରୁ 578 ମିଟର ଉଚ୍ଚତା, ସେରା ଡୋ ରିଓ ପ୍ରିଟୋରେ ସର୍ବାଧିକ 1,516 ମିଟର ଏବଂ କରରେଗୋ ବୋଚା ମୁହାଣରେ 330 ମିଟର ଉଚ୍ଚତା |
ଫେଲିସିଆନୋ ମିଗୁଏଲ୍ ଅବଦାଲା ଘରୋଇ ପ୍ରାକୃତିକ itage ତିହ୍ୟ ସଂରକ୍ଷଣ ସ୍ଥାନ: ଫେଲିସିଆନୋ ମିଗୁଏଲ୍ ଅବଦାଲା ଘରୋଇ ପ୍ରାକୃତିକ ହେରିଟେଜ୍ ରିଜର୍ଭ , ପୂର୍ବରୁ ଫାଜେଣ୍ଡା ମୋଣ୍ଟେସ୍ କ୍ଲାରୋସ୍ ଏବଂ ପରେ କାରାଟିଙ୍ଗା ବାୟୋଲୋଜିକାଲ୍ ଷ୍ଟେସନ୍ , ବ୍ରାଜିଲର ମିନାସ୍ ଜେରାଇସ୍ ରାଜ୍ୟରେ ଏକ ଘରୋଇ ମାଲିକାନା ସ୍ଥାୟୀ-ବ୍ୟବହାର ସଂରକ୍ଷିତ ଅଞ୍ଚଳ ଅଟେ | ଏଥିରେ ଆଟଲାଣ୍ଟିକ୍ ଫରେଷ୍ଟ ବାୟୋମର ଏକ ଉଦାହରଣ ଅଛି | ଏହି ରିଜର୍ଭରେ ବିରଳ ବଫି-ହେଡ୍ ମାରମୋସେଟ୍ ଏବଂ ଉତ୍ତର ମୁରୁକି ପଶମ ସ୍ପାଇଡର ମାଙ୍କଡ଼ର ଶେଷ ବନ୍ୟ ଜନସଂଖ୍ୟା ରହିଛି |
Cărătnău: ରୋମାନିଆର ଅନେକ ସଂସ୍ଥାକୁ Cărătnău ସୂଚାଇପାରେ : Cărătnău de Jos ଏବଂ Cărătnău de Sus, Buzău County Săruleşti Commune ର ଗ୍ରାମଗୁଡିକ | Cărătnău ନଦୀ |
ପେସିନାଗା (ନଦୀ): ପେସିନାଗା କିମ୍ବା ପେସେନାଗା ରୋମାନିଆର ସ୍ଲୋନିକ୍ ନଦୀର ଏକ ବାମ ଉପନଦୀ ଅଟେ | ଏହା Vintilă Vodă ରେ Slănic ରେ ନିର୍ଗତ ହୁଏ | ଏହାର ଲମ୍ବ 14 କିଲୋମିଟର (8.7 ମାଇଲ) ଏବଂ ଏହାର ବେସନ ଆକାର 58 କିଲୋମିଟର 2 (22 ବର୍ଗ ମାଇଲ) | ନିମ୍ନଲିଖିତ ଗ୍ରାମଗୁଡିକ ପେସିନାଗା ନଦୀ କୂଳରେ ଅବସ୍ଥିତ, ଉତ୍ସରୁ ମୁଖ ପର୍ଯ୍ୟନ୍ତ: Băltăgari, Sările, Sărulești, Cărătnău de Jos ଏବଂ Vintilă Vodă |
Sărulești, Buzău: Sărulești , ରୋମାନିଆର ମୁଣ୍ଟେନିଆର ବୁଜୁ କାଉଣ୍ଟିରେ ଏକ କମ୍ୟୁନିଟି | ଏହା ସାତୋଟି ଗାଁକୁ ନେଇ ଗଠିତ: Cărătnău de Jos, Cărătnău de Sus, Goicelu, Sările-Ctun, Sărulești, Valea Largă-Sărulești ଏବଂ Valea Stânei |
Sărulești, Buzău: Sărulești , ରୋମାନିଆର ମୁଣ୍ଟେନିଆର ବୁଜୁ କାଉଣ୍ଟିରେ ଏକ କମ୍ୟୁନିଟି | ଏହା ସାତୋଟି ଗାଁକୁ ନେଇ ଗଠିତ: Cărătnău de Jos, Cărătnău de Sus, Goicelu, Sările-Ctun, Sărulești, Valea Largă-Sărulești ଏବଂ Valea Stânei |
କାରାଟୋଲା ମନୋରଞ୍ଜନ ପାର୍କ: କାରାଟୋଲା ମନୋରଞ୍ଜନ ପାର୍କ ହେଉଛି ଅଷ୍ଟ୍ରେଲିଆର ଦକ୍ଷିଣ ଅଷ୍ଟ୍ରେଲିଆର ଏକ ସଂରକ୍ଷିତ ଅଞ୍ଚଳ ଯାହାକି ହସଲାମ ସହରର ଉତ୍ତରରେ ପ୍ରାୟ 0.5 କିଲୋମିଟର ଉତ୍ତରରେ ଏବଂ ଷ୍ଟ୍ରେକି ବାଇ ସହରଠାରୁ ପ୍ରାୟ 35 କିଲୋମିଟର ଉତ୍ତରରେ ଅବସ୍ଥିତ।
କେରାଟୋସିସ୍ ପିଲାରିସ୍: Keratosis pilaris ଏକ ସାଧାରଣ, autosomal-ପ୍ରତିପତିଶୀଳ, ଜେନେଟିକ ଚର୍ମ କେଶ follicles ର ଅବସ୍ଥା ଆଭା ବିଶେଷତା ହେଉଛି ସମ୍ଭବତଃ itchy, ଛୋଟ, gooseflesh-ପରି bumps, reddening କିମ୍ବା ପ୍ରଦାହ ଡିଗ୍ରୀ varying ସହିତ। ଏହା ପ୍ରାୟତ the ଉପର ବାହୁ, ଜଙ୍ଘ, ମୁହଁ, ପିଠି ଏବଂ ନିତୁର ବାହ୍ୟ ପାର୍ଶ୍ୱରେ ଦେଖାଯାଏ; କେପି ହାତ, ଏବଂ ଗୋଡର ଉପର, ପାର୍ଶ୍ୱ, କିମ୍ବା ଗ୍ଲାବ୍ରସ୍ (କେଶହୀନ) ଚର୍ମ ବ୍ୟତୀତ ଅନ୍ୟ ଶରୀରର ଅଂଶରେ ମଧ୍ୟ ହୋଇପାରେ | ପ୍ରାୟତ the କ୍ଷତଗୁଡ଼ିକ ଚେହେରାରେ ଦେଖାଯାଏ, ଯାହା ବ୍ରଣ ପାଇଁ ଭୁଲ ହୋଇପାରେ |
କେରାଟୋସିସ୍ ପିଲାରିସ୍: Keratosis pilaris ଏକ ସାଧାରଣ, autosomal-ପ୍ରତିପତିଶୀଳ, ଜେନେଟିକ ଚର୍ମ କେଶ follicles ର ଅବସ୍ଥା ଆଭା ବିଶେଷତା ହେଉଛି ସମ୍ଭବତଃ itchy, ଛୋଟ, gooseflesh-ପରି bumps, reddening କିମ୍ବା ପ୍ରଦାହ ଡିଗ୍ରୀ varying ସହିତ। ଏହା ପ୍ରାୟତ the ଉପର ବାହୁ, ଜଙ୍ଘ, ମୁହଁ, ପିଠି ଏବଂ ନିତୁର ବାହ୍ୟ ପାର୍ଶ୍ୱରେ ଦେଖାଯାଏ; କେପି ହାତ, ଏବଂ ଗୋଡର ଉପର, ପାର୍ଶ୍ୱ, କିମ୍ବା ଗ୍ଲାବ୍ରସ୍ (କେଶହୀନ) ଚର୍ମ ବ୍ୟତୀତ ଅନ୍ୟ ଶରୀରର ଅଂଶରେ ମଧ୍ୟ ହୋଇପାରେ | ପ୍ରାୟତ the କ୍ଷତଗୁଡ଼ିକ ଚେହେରାରେ ଦେଖାଯାଏ, ଯାହା ବ୍ରଣ ପାଇଁ ଭୁଲ ହୋଇପାରେ |
କରାଟ: କରାଟ , କରାଟ , କରେଟ୍ କିମ୍ବା କରୋଟ୍ ସୂଚିତ କରିପାରନ୍ତି:
କରାଟି: କରାଟି ହେଉଛି ଏକ ଇଟାଲୀୟ ଉପନାମ | ଉପନାମ ବିଶିଷ୍ଟ ଉଲ୍ଲେଖନୀୟ ବ୍ୟକ୍ତିମାନେ ଅନ୍ତର୍ଭୁକ୍ତ: କ୍ରିଷ୍ଟିଆନୋ କାରାଟି, ଇଟାଲୀୟ ଟେନିସ୍ ଖେଳାଳି | ଅଷ୍ଟ୍ରେଲୀୟ ରେସ ଡ୍ରାଇଭର ଆରୋନ କାରାଟି |
ଆରୋନ କରାଟୀ: ଆରୋନ କରାଟି ଜଣେ ଅଷ୍ଟ୍ରେଲୀୟ ରେସିଂ ଡ୍ରାଇଭର | ସେ ଅଷ୍ଟ୍ରେଲିୟା ଫର୍ମୁଲା 3 ସିରିଜରେ ସ୍ନାତକ ହାସଲ କରିବା ପୂର୍ବରୁ କାର୍ଟିଂରୁ ଅଷ୍ଟ୍ରେଲିୟ ଫର୍ମୁଲା ଫୋର୍ଡ ଚାମ୍ପିଅନସିପ୍ ପର୍ଯ୍ୟନ୍ତ ଅଗ୍ରଗତି କରିଥିଲେ ଯେଉଁଠାରେ ସେ 2005 ରେ ଚାମ୍ପିଅନ୍ ହୋଇଥିଲେ। ସେହି ଦିନଠାରୁ ସେ କ୍ରୀଡା କାରରେ ମଧ୍ୟମ ସଫଳତା ସହ ପ୍ରତିଦ୍ୱନ୍ଦ୍ୱିତା କରିଥିଲେ |
କାରାଟିନୋ: କାରାଟିନୋ ହେଉଛି ଏକ ଇଟାଲୀୟ ଉପନାମ | ଉପନାମ ବିଶିଷ୍ଟ ଉଲ୍ଲେଖନୀୟ ବ୍ୟକ୍ତିମାନେ ଅନ୍ତର୍ଭୁକ୍ତ: ଆଣ୍ଟୋନିଓ କାରାଟିନୋ, ଇଟାଲୀୟ ନାବିକ | ଡୋମେନିକୋ କାରାଟିନୋ (1920–2004), ଇଟାଲୀୟ ନାବିକ | ଜିଉସେପେ କାରାଟିନୋ (1919–2014), ଇଟାଲୀୟ ନାବିକ |
କାରାଟିନୋ: କାରାଟିନୋ ହେଉଛି ଏକ ଇଟାଲୀୟ ଉପନାମ | ଉପନାମ ବିଶିଷ୍ଟ ଉଲ୍ଲେଖନୀୟ ବ୍ୟକ୍ତିମାନେ ଅନ୍ତର୍ଭୁକ୍ତ: ଆଣ୍ଟୋନିଓ କାରାଟିନୋ, ଇଟାଲୀୟ ନାବିକ | ଡୋମେନିକୋ କାରାଟିନୋ (1920–2004), ଇଟାଲୀୟ ନାବିକ | ଜିଉସେପେ କାରାଟିନୋ (1919–2014), ଇଟାଲୀୟ ନାବିକ |
ଫ୍ରାନ୍ସିସ୍କୋ କାରାଟୋଲି: ଫ୍ରାନ୍ସସ୍କୋ କାରାଟୋଲି ଜଣେ ଇଟାଲୀୟ ବ୍ୟାସ୍ ବଫୋ , କିମ୍ବା ଅପେରା ବଫାର ଗାୟକ ଥିଲେ |
କାରାଟଙ୍କ, ମେନ୍: କାରାଟଙ୍କ ହେଉଛି ଆମେରିକାର ମେନେର ସୋମେରସେଟ କାଉଣ୍ଟିର ଏକ ସହର | 2010 ଜନଗଣନାରେ ଜନସଂଖ୍ୟା 69 ଥିଲା |
କାରାଟଙ୍କ, ମେନ୍: କାରାଟଙ୍କ ହେଉଛି ଆମେରିକାର ମେନେର ସୋମେରସେଟ କାଉଣ୍ଟିର ଏକ ସହର | 2010 ଜନଗଣନାରେ ଜନସଂଖ୍ୟା 69 ଥିଲା |
କାରାଟଙ୍କ, ମେନ୍: କାରାଟଙ୍କ ହେଉଛି ଆମେରିକାର ମେନେର ସୋମେରସେଟ କାଉଣ୍ଟିର ଏକ ସହର | 2010 ଜନଗଣନାରେ ଜନସଂଖ୍ୟା 69 ଥିଲା |
କାରାଟୁଙ୍କ ଜଳପ୍ରପାତ ପ୍ରତ୍ନତାତ୍ତ୍ୱିକ ଜିଲ୍ଲା: କାରାଟୁଙ୍କ ଜଳପ୍ରପାତ ପ୍ରତ୍ନତାତ୍ତ୍ୱିକ ଜିଲ୍ଲା ହେଉଛି ସୋଲେନ୍ , ମେନ୍ ଅଞ୍ଚଳରେ ଥିବା ପ୍ରାଚୀନ ଏବଂ histor ତିହାସିକ ପ୍ରତ୍ନତାତ୍ତ୍ୱିକ ସ୍ଥାନଗୁଡିକର ଏକ ଜଟିଳ | ୧ ss ୦ ଦଶକରେ ପ୍ରଥମେ ପ୍ରତ୍ନତାତ୍ତ୍ୱିକ ଭାବରେ ଗୁରୁତ୍ identified ପୂର୍ଣ ଭାବରେ ଚିହ୍ନଟ ହୋଇଥିଲା, 1980 ଦଶକ ପୂର୍ବରୁ ରାଜ୍ୟ ପ୍ରତ୍ନତତ୍ତ୍ୱବିତ୍ମାନେ ଏହି ସ୍ଥାନଟି ମ୍ୟାପ୍ କରିଥିଲେ | ସେହି ସମୟରେ ଏହା ଆଭ୍ୟନ୍ତରୀଣ ମେନ୍ରେ ପ୍ରତ୍ନତାତ୍ତ୍ୱିକ ମହତ୍ତ୍ of ର ଏକକ ବୃହତ ଜଟିଳ ଥିଲା, ଯାହା ଆର୍ଚିକ୍ ଠାରୁ ୟୁରୋପୀୟ ଯୋଗାଯୋଗ ସମୟ ପର୍ଯ୍ୟନ୍ତ ମାନବ କାର୍ଯ୍ୟକଳାପର ଏକ ସମୟକୁ ଅନ୍ତର୍ଭୁକ୍ତ କରିଥିଲା ​​| ୧ ac ଏକର (.5..5 ହେକ୍ଟର) କ୍ଷେତ୍ର 1986 ରେ Histor ତିହାସିକ ସ୍ଥାନଗୁଡିକର ଜାତୀୟ ରେଜିଷ୍ଟରରେ ତାଲିକାଭୁକ୍ତ ହୋଇଥିଲା |
କାରାଟୁଭା ନଦୀ: କାରାଟୁଭା ନଦୀ ଦକ୍ଷିଣ ବ୍ରାଜିଲର ପାରାନା ରାଜ୍ୟର ଏକ ନଦୀ | ଏହା କାଣ୍ଟୋ ନଦୀର ଏକ ଉପନଦୀ ଅଟେ |
କାରା: କାରୁ ଏକ ପୁରାଣ, ସାଧାରଣତ north ଉତ୍ତର-ପୂର୍ବ ଆର୍ଜେଣ୍ଟିନା କାହାଣୀରେ ଜଣାଶୁଣା |
କାରାଉରି: କାରାଉରି ହେଉଛି ବ୍ରାଜିଲର ଆମାଜନସ୍ ରାଜ୍ୟରେ ଅବସ୍ଥିତ ଏକ ପ ity ରପାଳିକା | ଏହାର ଜନସଂଖ୍ୟା 28,508 (2020) ଏବଂ ଏହାର କ୍ଷେତ୍ର 25,767 କିଲୋମିଟର |
କାରାଉରି ବିମାନବନ୍ଦର: କାରାଉରି ବିମାନବନ୍ଦର ହେଉଛି ବ୍ରାଜିଲର କାରାଓରି ସେବା କରୁଥିବା ବିମାନବନ୍ଦର |
କାରାବାସ୍: କାରାବାସ୍ ବ୍ରାଜିଲର ଉତ୍ତର-ପୂର୍ବ ଅଞ୍ଚଳର ପାରାବା ରାଜ୍ୟର ଏକ ପ ity ରପାଳିକା ଅଟେ |
କାରାବାସ୍, ରିଓ ଗ୍ରାଣ୍ଡେ ଡୋ ନର୍ଟେ: କାରାବାସ୍ ବ୍ରାଜିଲର ଉତ୍ତର-ପୂର୍ବ ଅଞ୍ଚଳର ରିଓ ଗ୍ରାଣ୍ଡେ ଡୋ ନର୍ଟେ ରାଜ୍ୟର ଏକ ପ ity ରପାଳିକା ଅଟେ |
Caraúbas do Piauí: Caraúbas do Piauí ବ୍ରାଜିଲର ଉତ୍ତର-ପୂର୍ବ ଅଞ୍ଚଳରେ ପିଆଉଇର ଏକ ପ ity ରପାଳିକା |
କାରାଉସିୟସ୍: ମାର୍କସ୍ ଆରେଲିୟସ୍ ମାଉସାଉସ୍ କାରାଉସିୟସ୍ ତୃତୀୟ ଶତାବ୍ଦୀରେ ରୋମାନ୍ ସାମ୍ରାଜ୍ୟର ଜଣେ ସାମରିକ କମାଣ୍ଡର ଥିଲେ। ସେ ବେଲଜିୟମ ଗାଲର ଜଣେ ମେନାପିଆନ୍ ଥିଲେ, ଯିଏ କି କାରାସିଆନ୍ ବିଦ୍ରୋହ ସମୟରେ 286 ମସିହାରେ କ୍ଷମତା ହାସଲ କରିଥିଲେ ଏବଂ ନିଜକୁ ବ୍ରିଟେନ ଏବଂ ଉତ୍ତର ଗାଲରେ ସମ୍ରାଟ ଘୋଷଣା କରିଥିଲେ। 273 ରେ ବାଟାଭିଆନ୍ ପୋଷ୍ଟମସ୍ ର ଗାଲିକ୍ ସାମ୍ରାଜ୍ୟ ସମାପ୍ତ ହେବାର 13 ବର୍ଷ ପରେ ସେ ଏହା କରିଥିଲେ। ଅର୍ଥମନ୍ତ୍ରୀ ଆଲେକ୍ଟସ୍ଙ୍କ ଦ୍ୱାରା ହତ୍ୟା ହେବା ପୂର୍ବରୁ ସେ ନିଜ ପାଇଁ "ଉତ୍ତରର ସମ୍ରାଟ" ନାମ ତିଆରି କରି ସାତ ବର୍ଷ ପର୍ଯ୍ୟନ୍ତ କ୍ଷମତାରେ ରହିଥିଲେ।
Prosopis kuntzei: ପ୍ରୋସୋପିସ୍ କୁଣ୍ଟଜେଇ ହେଉଛି ଦକ୍ଷିଣ ଆମେରିକାର ଲେଗୁମିନସ୍ ଗଛ ପ୍ରଜାତି ଯାହା ଆର୍ଜେଣ୍ଟିନା, ବୋଲିଭିଆ, ଏବଂ ପାରାଗୁଏର ପଶ୍ଚିମ ଦିଗରେ ଥିବା ଗ୍ରାନ୍ ଚାକୋ ଜଙ୍ଗଲରେ ବାସ କରେ, ଯେଉଁଠାରେ ଏହା ପ୍ରାକୃତିକ ଉପାଦାନ ଭାବରେ କାର୍ଯ୍ୟ କରିଥାଏ | ଏହା ନିକଟସ୍ଥ ଚାରଣ ସାବାନାକୁ ଉପନିବେଶ କରିବାରେ ସକ୍ଷମ ହୋଇଛି | ଏହାକୁ ସାଧାରଣତ it itín, palo mataco, carandá କିମ୍ବା barba de tigre କୁହାଯାଏ | ଏହା ଶୁଷ୍କ ଜଳବାୟୁ ସହିତ ଖାପ ଖୁଆଇଛି, କିନ୍ତୁ ଦୀର୍ଘ ସମୟ ପର୍ଯ୍ୟନ୍ତ ବନ୍ୟା ପରିସ୍ଥିତିରୁ ବଞ୍ଚିପାରେ |
Prosopis kuntzei: ପ୍ରୋସୋପିସ୍ କୁଣ୍ଟଜେଇ ହେଉଛି ଦକ୍ଷିଣ ଆମେରିକାର ଲେଗୁମିନସ୍ ଗଛ ପ୍ରଜାତି ଯାହା ଆର୍ଜେଣ୍ଟିନା, ବୋଲିଭିଆ, ଏବଂ ପାରାଗୁଏର ପଶ୍ଚିମ ଦିଗରେ ଥିବା ଗ୍ରାନ୍ ଚାକୋ ଜଙ୍ଗଲରେ ବାସ କରେ, ଯେଉଁଠାରେ ଏହା ପ୍ରାକୃତିକ ଉପାଦାନ ଭାବରେ କାର୍ଯ୍ୟ କରିଥାଏ | ଏହା ନିକଟସ୍ଥ ଚାରଣ ସାବାନାକୁ ଉପନିବେଶ କରିବାରେ ସକ୍ଷମ ହୋଇଛି | ଏହାକୁ ସାଧାରଣତ it itín, palo mataco, carandá କିମ୍ବା barba de tigre କୁହାଯାଏ | ଏହା ଶୁଷ୍କ ଜଳବାୟୁ ସହିତ ଖାପ ଖୁଆଇଛି, କିନ୍ତୁ ଦୀର୍ଘ ସମୟ ପର୍ଯ୍ୟନ୍ତ ବନ୍ୟା ପରିସ୍ଥିତିରୁ ବଞ୍ଚିପାରେ |
Prosopis kuntzei: ପ୍ରୋସୋପିସ୍ କୁଣ୍ଟଜେଇ ହେଉଛି ଦକ୍ଷିଣ ଆମେରିକାର ଲେଗୁମିନସ୍ ଗଛ ପ୍ରଜାତି ଯାହା ଆର୍ଜେଣ୍ଟିନା, ବୋଲିଭିଆ, ଏବଂ ପାରାଗୁଏର ପଶ୍ଚିମ ଦିଗରେ ଥିବା ଗ୍ରାନ୍ ଚାକୋ ଜଙ୍ଗଲରେ ବାସ କରେ, ଯେଉଁଠାରେ ଏହା ପ୍ରାକୃତିକ ଉପାଦାନ ଭାବରେ କାର୍ଯ୍ୟ କରିଥାଏ | ଏହା ନିକଟସ୍ଥ ଚାରଣ ସାବାନାକୁ ଉପନିବେଶ କରିବାରେ ସକ୍ଷମ ହୋଇଛି | ଏହାକୁ ସାଧାରଣତ it itín, palo mataco, carandá କିମ୍ବା barba de tigre କୁହାଯାଏ | ଏହା ଶୁଷ୍କ ଜଳବାୟୁ ସହିତ ଖାପ ଖୁଆଇଛି, କିନ୍ତୁ ଦୀର୍ଘ ସମୟ ପର୍ଯ୍ୟନ୍ତ ବନ୍ୟା ପରିସ୍ଥିତିରୁ ବଞ୍ଚିପାରେ |
Prosopis kuntzei: ପ୍ରୋସୋପିସ୍ କୁଣ୍ଟଜେଇ ହେଉଛି ଦକ୍ଷିଣ ଆମେରିକାର ଲେଗୁମିନସ୍ ଗଛ ପ୍ରଜାତି ଯାହା ଆର୍ଜେଣ୍ଟିନା, ବୋଲିଭିଆ, ଏବଂ ପାରାଗୁଏର ପଶ୍ଚିମ ଦିଗରେ ଥିବା ଗ୍ରାନ୍ ଚାକୋ ଜଙ୍ଗଲରେ ବାସ କରେ, ଯେଉଁଠାରେ ଏହା ପ୍ରାକୃତିକ ଉପାଦାନ ଭାବରେ କାର୍ଯ୍ୟ କରିଥାଏ | ଏହା ନିକଟସ୍ଥ ଚାରଣ ସାବାନାକୁ ଉପନିବେଶ କରିବାରେ ସକ୍ଷମ ହୋଇଛି | ଏହାକୁ ସାଧାରଣତ it itín, palo mataco, carandá କିମ୍ବା barba de tigre କୁହାଯାଏ | ଏହା ଶୁଷ୍କ ଜଳବାୟୁ ସହିତ ଖାପ ଖୁଆଇଛି, କିନ୍ତୁ ଦୀର୍ଘ ସମୟ ପର୍ଯ୍ୟନ୍ତ ବନ୍ୟା ପରିସ୍ଥିତିରୁ ବଞ୍ଚିପାରେ |
କାରାଲା: 2560 ଜନସଂଖ୍ୟା ବିଶିଷ୍ଟ ରୋମାନିଆର ଓଲଟେନିଆର ଡଲଜ୍ କାଉଣ୍ଟିରେ କାରାଲା ଏକ କମ୍ୟୁନିଟି | ଏହା ଏକ ଗାଁ, କାରୁଲାକୁ ନେଇ ଗଠିତ |
କାରାଲା: 2560 ଜନସଂଖ୍ୟା ବିଶିଷ୍ଟ ରୋମାନିଆର ଓଲଟେନିଆର ଡଲଜ୍ କାଉଣ୍ଟିରେ କାରାଲା ଏକ କମ୍ୟୁନିଟି | ଏହା ଏକ ଗାଁ, କାରୁଲାକୁ ନେଇ ଗଠିତ |
କାରାଲା (ନଦୀ): କାରାଉଲା ସୁକେଭା ନଦୀର ଏକ ବାମ ଉପନଦୀ ଅଟେ | ଏହାର ଉତ୍ସ ୟୁକ୍ରେନର ଚେର୍ନିଭ୍ଟି ଓବ୍ଲାଷ୍ଟର ଚେର୍ନିଭଟସି ରାଏନରେ ଅବସ୍ଥିତ | ଏହା ପରେ ନଦୀ ସୀମା ଅତିକ୍ରମ କରି ରୋମାନିଆକୁ ଯାଇ ଭିକୋଭୁ ଦେ ସୁସ୍ ଗାଁ ନିକଟରେ ଥିବା ସୁକେଭା ସହିତ ଯୋଗ ଦେଲା | ରୋମାନିଆରେ ଏହାର ଲମ୍ବ 4 କିଲୋମିଟର (2.5 ମାଇଲ) ଏବଂ ଏହାର ବେସନ ଆକାର 4 କିଲୋମିଟର 2 (1.5 ବର୍ଗ ମାଇଲ) |
କାରାଲା (ନଦୀ): କାରାଉଲା ସୁକେଭା ନଦୀର ଏକ ବାମ ଉପନଦୀ ଅଟେ | ଏହାର ଉତ୍ସ ୟୁକ୍ରେନର ଚେର୍ନିଭ୍ଟି ଓବ୍ଲାଷ୍ଟର ଚେର୍ନିଭଟସି ରାଏନରେ ଅବସ୍ଥିତ | ଏହା ପରେ ନଦୀ ସୀମା ଅତିକ୍ରମ କରି ରୋମାନିଆକୁ ଯାଇ ଭିକୋଭୁ ଦେ ସୁସ୍ ଗାଁ ନିକଟରେ ଥିବା ସୁକେଭା ସହିତ ଯୋଗ ଦେଲା | ରୋମାନିଆରେ ଏହାର ଲମ୍ବ 4 କିଲୋମିଟର (2.5 ମାଇଲ) ଏବଂ ଏହାର ବେସନ ଆକାର 4 କିଲୋମିଟର 2 (1.5 ବର୍ଗ ମାଇଲ) |
କାରାଲୁନ୍ ନଦୀ: କାରାଲୁନ୍ ନଦୀ ହେଉଛି ପୂର୍ବ ତିମୋର ଏକ ନଦୀ | ଏହା ଆଇନାରୋ ଜିଲ୍ଲା ଏବଂ ମନୁଫାହି ଜିଲ୍ଲା ମଧ୍ୟରେ ସୀମା ଏବଂ ତିମୋର ସାଗରରେ ଦକ୍ଷିଣକୁ ପ୍ରବାହିତ ହେଉଛି |
କାରାଉନ୍ ରିଡ୍: କାରାଉନ୍ ରିଡ୍ ହେଉଛି ଏକ ଆମେରିକୀୟ ଫୁଟବଲ୍ ପ୍ରତିରକ୍ଷା ଟ୍ୟାକ୍ ଯିଏ ଏକ ମାଗଣା ଏଜେଣ୍ଟ | ସେ 2014 NFL ଡ୍ରାଫ୍ଟର ପଞ୍ଚମ ରାଉଣ୍ଡରେ ଡେଟ୍ରୋଇଟ୍ ଲାୟନ୍ସ ଦ୍ୱାରା ପ୍ରସ୍ତୁତ ହୋଇଥିଲେ | ସେ ପ୍ରିନ୍ସଟନ୍ରେ କଲେଜ ଫୁଟବଲ୍ ଖେଳିଥିଲେ | ସେ ସାନ ଡିଏଗୋ ଚାର୍ଜର୍ସ, ୱାଶିଂଟନ୍ ରେଡକ୍ରସ୍, ଇଣ୍ଡିଆନାପଲିସ୍ କଲ୍ଟସ୍ ଏବଂ ଡାଲାସ୍ କାଉବୟସ୍ ସଦସ୍ୟ ମଧ୍ୟ ରହିଛନ୍ତି।