Arith, Arith, Savoie, ARITH Symposium on Computer Arithmetic

ଆରିଥ: ଆରିଥ୍ ରେଫର୍ କରିପାରନ୍ତି:
ଆରିଥ, ସାଭୋଇ: ଆରିଥ ଦକ୍ଷିଣ-ପୂର୍ବ ଫ୍ରାନ୍ସର ଆଭର୍ନେ-ରୋନ୍-ଆଲପ୍ସ ଅଞ୍ଚଳର ସାଭୋଇ ବିଭାଗରେ ଏକ କମ୍ୟୁନିଟି |
କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ଉପରେ ARITH ସିମ୍ପୋଜିମ୍: କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ( ARITH ) ଉପରେ IEEE ଆନ୍ତର୍ଜାତୀୟ ସମ୍ମିଳନୀ ହେଉଛି କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ କ୍ଷେତ୍ରରେ ଏକ ସମ୍ମିଳନୀ | ଏହି ସମ୍ମିଳନୀ 1969 ରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା, ପ୍ରାରମ୍ଭରେ ତିନିବର୍ଷର ଇଭେଣ୍ଟ ଭାବରେ, ତାପରେ ଆବିନାଲ୍ ଇଭେଣ୍ଟ ଭାବରେ ଏବଂ ଶେଷରେ, 2015 ଠାରୁ ବାର୍ଷିକ ସମ୍ମିଳନୀ ଭାବରେ |
କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ଉପରେ ARITH ସିମ୍ପୋଜିମ୍: କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ( ARITH ) ଉପରେ IEEE ଆନ୍ତର୍ଜାତୀୟ ସମ୍ମିଳନୀ ହେଉଛି କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ କ୍ଷେତ୍ରରେ ଏକ ସମ୍ମିଳନୀ | ଏହି ସମ୍ମିଳନୀ 1969 ରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା, ପ୍ରାରମ୍ଭରେ ତିନିବର୍ଷର ଇଭେଣ୍ଟ ଭାବରେ, ତାପରେ ଆବିନାଲ୍ ଇଭେଣ୍ଟ ଭାବରେ ଏବଂ ଶେଷରେ, 2015 ଠାରୁ ବାର୍ଷିକ ସମ୍ମିଳନୀ ଭାବରେ |
କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ଉପରେ ARITH ସିମ୍ପୋଜିମ୍: କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ( ARITH ) ଉପରେ IEEE ଆନ୍ତର୍ଜାତୀୟ ସମ୍ମିଳନୀ ହେଉଛି କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ କ୍ଷେତ୍ରରେ ଏକ ସମ୍ମିଳନୀ | ଏହି ସମ୍ମିଳନୀ 1969 ରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା, ପ୍ରାରମ୍ଭରେ ତିନିବର୍ଷର ଇଭେଣ୍ଟ ଭାବରେ, ତାପରେ ଆବିନାଲ୍ ଇଭେଣ୍ଟ ଭାବରେ ଏବଂ ଶେଷରେ, 2015 ଠାରୁ ବାର୍ଷିକ ସମ୍ମିଳନୀ ଭାବରେ |
କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ଉପରେ ARITH ସିମ୍ପୋଜିମ୍: କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ( ARITH ) ଉପରେ IEEE ଆନ୍ତର୍ଜାତୀୟ ସମ୍ମିଳନୀ ହେଉଛି କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ କ୍ଷେତ୍ରରେ ଏକ ସମ୍ମିଳନୀ | ଏହି ସମ୍ମିଳନୀ 1969 ରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା, ପ୍ରାରମ୍ଭରେ ତିନିବର୍ଷର ଇଭେଣ୍ଟ ଭାବରେ, ତାପରେ ଆବିନାଲ୍ ଇଭେଣ୍ଟ ଭାବରେ ଏବଂ ଶେଷରେ, 2015 ଠାରୁ ବାର୍ଷିକ ସମ୍ମିଳନୀ ଭାବରେ |
କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ଉପରେ ARITH ସିମ୍ପୋଜିମ୍: କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ( ARITH ) ଉପରେ IEEE ଆନ୍ତର୍ଜାତୀୟ ସମ୍ମିଳନୀ ହେଉଛି କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ କ୍ଷେତ୍ରରେ ଏକ ସମ୍ମିଳନୀ | ଏହି ସମ୍ମିଳନୀ 1969 ରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା, ପ୍ରାରମ୍ଭରେ ତିନିବର୍ଷର ଇଭେଣ୍ଟ ଭାବରେ, ତାପରେ ଆବିନାଲ୍ ଇଭେଣ୍ଟ ଭାବରେ ଏବଂ ଶେଷରେ, 2015 ଠାରୁ ବାର୍ଷିକ ସମ୍ମିଳନୀ ଭାବରେ |
କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ଉପରେ ARITH ସିମ୍ପୋଜିମ୍: କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ( ARITH ) ଉପରେ IEEE ଆନ୍ତର୍ଜାତୀୟ ସମ୍ମିଳନୀ ହେଉଛି କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ କ୍ଷେତ୍ରରେ ଏକ ସମ୍ମିଳନୀ | ଏହି ସମ୍ମିଳନୀ 1969 ରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା, ପ୍ରାରମ୍ଭରେ ତିନିବର୍ଷର ଇଭେଣ୍ଟ ଭାବରେ, ତାପରେ ଆବିନାଲ୍ ଇଭେଣ୍ଟ ଭାବରେ ଏବଂ ଶେଷରେ, 2015 ଠାରୁ ବାର୍ଷିକ ସମ୍ମିଳନୀ ଭାବରେ |
କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ଉପରେ ARITH ସିମ୍ପୋଜିମ୍: କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ( ARITH ) ଉପରେ IEEE ଆନ୍ତର୍ଜାତୀୟ ସମ୍ମିଳନୀ ହେଉଛି କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ କ୍ଷେତ୍ରରେ ଏକ ସମ୍ମିଳନୀ | ଏହି ସମ୍ମିଳନୀ 1969 ରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା, ପ୍ରାରମ୍ଭରେ ତିନିବର୍ଷର ଇଭେଣ୍ଟ ଭାବରେ, ତାପରେ ଆବିନାଲ୍ ଇଭେଣ୍ଟ ଭାବରେ ଏବଂ ଶେଷରେ, 2015 ଠାରୁ ବାର୍ଷିକ ସମ୍ମିଳନୀ ଭାବରେ |
କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ଉପରେ ARITH ସିମ୍ପୋଜିମ୍: କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ( ARITH ) ଉପରେ IEEE ଆନ୍ତର୍ଜାତୀୟ ସମ୍ମିଳନୀ ହେଉଛି କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ କ୍ଷେତ୍ରରେ ଏକ ସମ୍ମିଳନୀ | ଏହି ସମ୍ମିଳନୀ 1969 ରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା, ପ୍ରାରମ୍ଭରେ ତିନିବର୍ଷର ଇଭେଣ୍ଟ ଭାବରେ, ତାପରେ ଆବିନାଲ୍ ଇଭେଣ୍ଟ ଭାବରେ ଏବଂ ଶେଷରେ, 2015 ଠାରୁ ବାର୍ଷିକ ସମ୍ମିଳନୀ ଭାବରେ |
କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ଉପରେ ARITH ସିମ୍ପୋଜିମ୍: କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ( ARITH ) ଉପରେ IEEE ଆନ୍ତର୍ଜାତୀୟ ସମ୍ମିଳନୀ ହେଉଛି କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ କ୍ଷେତ୍ରରେ ଏକ ସମ୍ମିଳନୀ | ଏହି ସମ୍ମିଳନୀ 1969 ରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା, ପ୍ରାରମ୍ଭରେ ତିନିବର୍ଷର ଇଭେଣ୍ଟ ଭାବରେ, ତାପରେ ଆବିନାଲ୍ ଇଭେଣ୍ଟ ଭାବରେ ଏବଂ ଶେଷରେ, 2015 ଠାରୁ ବାର୍ଷିକ ସମ୍ମିଳନୀ ଭାବରେ |
କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ଉପରେ ARITH ସିମ୍ପୋଜିମ୍: କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ( ARITH ) ଉପରେ IEEE ଆନ୍ତର୍ଜାତୀୟ ସମ୍ମିଳନୀ ହେଉଛି କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ କ୍ଷେତ୍ରରେ ଏକ ସମ୍ମିଳନୀ | ଏହି ସମ୍ମିଳନୀ 1969 ରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା, ପ୍ରାରମ୍ଭରେ ତିନିବର୍ଷର ଇଭେଣ୍ଟ ଭାବରେ, ତାପରେ ଆବିନାଲ୍ ଇଭେଣ୍ଟ ଭାବରେ ଏବଂ ଶେଷରେ, 2015 ଠାରୁ ବାର୍ଷିକ ସମ୍ମିଳନୀ ଭାବରେ |
କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ଉପରେ ARITH ସିମ୍ପୋଜିମ୍: କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ( ARITH ) ଉପରେ IEEE ଆନ୍ତର୍ଜାତୀୟ ସମ୍ମିଳନୀ ହେଉଛି କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ କ୍ଷେତ୍ରରେ ଏକ ସମ୍ମିଳନୀ | ଏହି ସମ୍ମିଳନୀ 1969 ରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା, ପ୍ରାରମ୍ଭରେ ତିନିବର୍ଷର ଇଭେଣ୍ଟ ଭାବରେ, ତାପରେ ଆବିନାଲ୍ ଇଭେଣ୍ଟ ଭାବରେ ଏବଂ ଶେଷରେ, 2015 ଠାରୁ ବାର୍ଷିକ ସମ୍ମିଳନୀ ଭାବରେ |
କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ଉପରେ ARITH ସିମ୍ପୋଜିମ୍: କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ( ARITH ) ଉପରେ IEEE ଆନ୍ତର୍ଜାତୀୟ ସମ୍ମିଳନୀ ହେଉଛି କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ କ୍ଷେତ୍ରରେ ଏକ ସମ୍ମିଳନୀ | ଏହି ସମ୍ମିଳନୀ 1969 ରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା, ପ୍ରାରମ୍ଭରେ ତିନିବର୍ଷର ଇଭେଣ୍ଟ ଭାବରେ, ତାପରେ ଆବିନାଲ୍ ଇଭେଣ୍ଟ ଭାବରେ ଏବଂ ଶେଷରେ, 2015 ଠାରୁ ବାର୍ଷିକ ସମ୍ମିଳନୀ ଭାବରେ |
କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ଉପରେ ARITH ସିମ୍ପୋଜିମ୍: କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ( ARITH ) ଉପରେ IEEE ଆନ୍ତର୍ଜାତୀୟ ସମ୍ମିଳନୀ ହେଉଛି କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ କ୍ଷେତ୍ରରେ ଏକ ସମ୍ମିଳନୀ | ଏହି ସମ୍ମିଳନୀ 1969 ରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା, ପ୍ରାରମ୍ଭରେ ତିନିବର୍ଷର ଇଭେଣ୍ଟ ଭାବରେ, ତାପରେ ଆବିନାଲ୍ ଇଭେଣ୍ଟ ଭାବରେ ଏବଂ ଶେଷରେ, 2015 ଠାରୁ ବାର୍ଷିକ ସମ୍ମିଳନୀ ଭାବରେ |
କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ଉପରେ ARITH ସିମ୍ପୋଜିମ୍: କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ( ARITH ) ଉପରେ IEEE ଆନ୍ତର୍ଜାତୀୟ ସମ୍ମିଳନୀ ହେଉଛି କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ କ୍ଷେତ୍ରରେ ଏକ ସମ୍ମିଳନୀ | ଏହି ସମ୍ମିଳନୀ 1969 ରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା, ପ୍ରାରମ୍ଭରେ ତିନିବର୍ଷର ଇଭେଣ୍ଟ ଭାବରେ, ତାପରେ ଆବିନାଲ୍ ଇଭେଣ୍ଟ ଭାବରେ ଏବଂ ଶେଷରେ, 2015 ଠାରୁ ବାର୍ଷିକ ସମ୍ମିଳନୀ ଭାବରେ |
କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ଉପରେ ARITH ସିମ୍ପୋଜିମ୍: କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ( ARITH ) ଉପରେ IEEE ଆନ୍ତର୍ଜାତୀୟ ସମ୍ମିଳନୀ ହେଉଛି କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ କ୍ଷେତ୍ରରେ ଏକ ସମ୍ମିଳନୀ | ଏହି ସମ୍ମିଳନୀ 1969 ରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା, ପ୍ରାରମ୍ଭରେ ତିନିବର୍ଷର ଇଭେଣ୍ଟ ଭାବରେ, ତାପରେ ଆବିନାଲ୍ ଇଭେଣ୍ଟ ଭାବରେ ଏବଂ ଶେଷରେ, 2015 ଠାରୁ ବାର୍ଷିକ ସମ୍ମିଳନୀ ଭାବରେ |
କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ଉପରେ ARITH ସିମ୍ପୋଜିମ୍: କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ( ARITH ) ଉପରେ IEEE ଆନ୍ତର୍ଜାତୀୟ ସମ୍ମିଳନୀ ହେଉଛି କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ କ୍ଷେତ୍ରରେ ଏକ ସମ୍ମିଳନୀ | ଏହି ସମ୍ମିଳନୀ 1969 ରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା, ପ୍ରାରମ୍ଭରେ ତିନିବର୍ଷର ଇଭେଣ୍ଟ ଭାବରେ, ତାପରେ ଆବିନାଲ୍ ଇଭେଣ୍ଟ ଭାବରେ ଏବଂ ଶେଷରେ, 2015 ଠାରୁ ବାର୍ଷିକ ସମ୍ମିଳନୀ ଭାବରେ |
କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ଉପରେ ARITH ସିମ୍ପୋଜିମ୍: କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ( ARITH ) ଉପରେ IEEE ଆନ୍ତର୍ଜାତୀୟ ସମ୍ମିଳନୀ ହେଉଛି କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ କ୍ଷେତ୍ରରେ ଏକ ସମ୍ମିଳନୀ | ଏହି ସମ୍ମିଳନୀ 1969 ରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା, ପ୍ରାରମ୍ଭରେ ତିନିବର୍ଷର ଇଭେଣ୍ଟ ଭାବରେ, ତାପରେ ଆବିନାଲ୍ ଇଭେଣ୍ଟ ଭାବରେ ଏବଂ ଶେଷରେ, 2015 ଠାରୁ ବାର୍ଷିକ ସମ୍ମିଳନୀ ଭାବରେ |
କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ଉପରେ ARITH ସିମ୍ପୋଜିମ୍: କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ( ARITH ) ଉପରେ IEEE ଆନ୍ତର୍ଜାତୀୟ ସମ୍ମିଳନୀ ହେଉଛି କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ କ୍ଷେତ୍ରରେ ଏକ ସମ୍ମିଳନୀ | ଏହି ସମ୍ମିଳନୀ 1969 ରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା, ପ୍ରାରମ୍ଭରେ ତିନିବର୍ଷର ଇଭେଣ୍ଟ ଭାବରେ, ତାପରେ ଆବିନାଲ୍ ଇଭେଣ୍ଟ ଭାବରେ ଏବଂ ଶେଷରେ, 2015 ଠାରୁ ବାର୍ଷିକ ସମ୍ମିଳନୀ ଭାବରେ |
କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ଉପରେ ARITH ସିମ୍ପୋଜିମ୍: କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ( ARITH ) ଉପରେ IEEE ଆନ୍ତର୍ଜାତୀୟ ସମ୍ମିଳନୀ ହେଉଛି କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ କ୍ଷେତ୍ରରେ ଏକ ସମ୍ମିଳନୀ | ଏହି ସମ୍ମିଳନୀ 1969 ରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା, ପ୍ରାରମ୍ଭରେ ତିନିବର୍ଷର ଇଭେଣ୍ଟ ଭାବରେ, ତାପରେ ଆବିନାଲ୍ ଇଭେଣ୍ଟ ଭାବରେ ଏବଂ ଶେଷରେ, 2015 ଠାରୁ ବାର୍ଷିକ ସମ୍ମିଳନୀ ଭାବରେ |
କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ଉପରେ ARITH ସିମ୍ପୋଜିମ୍: କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ( ARITH ) ଉପରେ IEEE ଆନ୍ତର୍ଜାତୀୟ ସମ୍ମିଳନୀ ହେଉଛି କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ କ୍ଷେତ୍ରରେ ଏକ ସମ୍ମିଳନୀ | ଏହି ସମ୍ମିଳନୀ 1969 ରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା, ପ୍ରାରମ୍ଭରେ ତିନିବର୍ଷର ଇଭେଣ୍ଟ ଭାବରେ, ତାପରେ ଆବିନାଲ୍ ଇଭେଣ୍ଟ ଭାବରେ ଏବଂ ଶେଷରେ, 2015 ଠାରୁ ବାର୍ଷିକ ସମ୍ମିଳନୀ ଭାବରେ |
କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ଉପରେ ARITH ସିମ୍ପୋଜିମ୍: କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ( ARITH ) ଉପରେ IEEE ଆନ୍ତର୍ଜାତୀୟ ସମ୍ମିଳନୀ ହେଉଛି କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ କ୍ଷେତ୍ରରେ ଏକ ସମ୍ମିଳନୀ | ଏହି ସମ୍ମିଳନୀ 1969 ରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା, ପ୍ରାରମ୍ଭରେ ତିନିବର୍ଷର ଇଭେଣ୍ଟ ଭାବରେ, ତାପରେ ଆବିନାଲ୍ ଇଭେଣ୍ଟ ଭାବରେ ଏବଂ ଶେଷରେ, 2015 ଠାରୁ ବାର୍ଷିକ ସମ୍ମିଳନୀ ଭାବରେ |
କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ଉପରେ ARITH ସିମ୍ପୋଜିମ୍: କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ( ARITH ) ଉପରେ IEEE ଆନ୍ତର୍ଜାତୀୟ ସମ୍ମିଳନୀ ହେଉଛି କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ କ୍ଷେତ୍ରରେ ଏକ ସମ୍ମିଳନୀ | ଏହି ସମ୍ମିଳନୀ 1969 ରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା, ପ୍ରାରମ୍ଭରେ ତିନିବର୍ଷର ଇଭେଣ୍ଟ ଭାବରେ, ତାପରେ ଆବିନାଲ୍ ଇଭେଣ୍ଟ ଭାବରେ ଏବଂ ଶେଷରେ, 2015 ଠାରୁ ବାର୍ଷିକ ସମ୍ମିଳନୀ ଭାବରେ |
କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ଉପରେ ARITH ସିମ୍ପୋଜିମ୍: କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ( ARITH ) ଉପରେ IEEE ଆନ୍ତର୍ଜାତୀୟ ସମ୍ମିଳନୀ ହେଉଛି କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ କ୍ଷେତ୍ରରେ ଏକ ସମ୍ମିଳନୀ | ଏହି ସମ୍ମିଳନୀ 1969 ରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା, ପ୍ରାରମ୍ଭରେ ତିନିବର୍ଷର ଇଭେଣ୍ଟ ଭାବରେ, ତାପରେ ଆବିନାଲ୍ ଇଭେଣ୍ଟ ଭାବରେ ଏବଂ ଶେଷରେ, 2015 ଠାରୁ ବାର୍ଷିକ ସମ୍ମିଳନୀ ଭାବରେ |
କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ଉପରେ ARITH ସିମ୍ପୋଜିମ୍: କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ( ARITH ) ଉପରେ IEEE ଆନ୍ତର୍ଜାତୀୟ ସମ୍ମିଳନୀ ହେଉଛି କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ କ୍ଷେତ୍ରରେ ଏକ ସମ୍ମିଳନୀ | ଏହି ସମ୍ମିଳନୀ 1969 ରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା, ପ୍ରାରମ୍ଭରେ ତିନିବର୍ଷର ଇଭେଣ୍ଟ ଭାବରେ, ତାପରେ ଆବିନାଲ୍ ଇଭେଣ୍ଟ ଭାବରେ ଏବଂ ଶେଷରେ, 2015 ଠାରୁ ବାର୍ଷିକ ସମ୍ମିଳନୀ ଭାବରେ |
କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ଉପରେ ARITH ସିମ୍ପୋଜିମ୍: କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ( ARITH ) ଉପରେ IEEE ଆନ୍ତର୍ଜାତୀୟ ସମ୍ମିଳନୀ ହେଉଛି କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ କ୍ଷେତ୍ରରେ ଏକ ସମ୍ମିଳନୀ | ଏହି ସମ୍ମିଳନୀ 1969 ରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା, ପ୍ରାରମ୍ଭରେ ତିନିବର୍ଷର ଇଭେଣ୍ଟ ଭାବରେ, ତାପରେ ଆବିନାଲ୍ ଇଭେଣ୍ଟ ଭାବରେ ଏବଂ ଶେଷରେ, 2015 ଠାରୁ ବାର୍ଷିକ ସମ୍ମିଳନୀ ଭାବରେ |
କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ଉପରେ ARITH ସିମ୍ପୋଜିମ୍: କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ ( ARITH ) ଉପରେ IEEE ଆନ୍ତର୍ଜାତୀୟ ସମ୍ମିଳନୀ ହେଉଛି କମ୍ପ୍ୟୁଟର ଆରିଥମେଟିକ୍ କ୍ଷେତ୍ରରେ ଏକ ସମ୍ମିଳନୀ | ଏହି ସମ୍ମିଳନୀ 1969 ରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା, ପ୍ରାରମ୍ଭରେ ତିନିବର୍ଷର ଇଭେଣ୍ଟ ଭାବରେ, ତାପରେ ଆବିନାଲ୍ ଇଭେଣ୍ଟ ଭାବରେ ଏବଂ ଶେଷରେ, 2015 ଠାରୁ ବାର୍ଷିକ ସମ୍ମିଳନୀ ଭାବରେ |
ଆରିଥା ୱାନ୍ ହର୍କ: ଆରିଥା ଭାନ୍ ହର୍କ ,, ଜଣେ କାନାଡିୟ ଲେଖକ, ସମାଲୋଚକ, ସମ୍ପାଦକ, ଜନ ବୁଦ୍ଧିଜୀବୀ ଏବଂ ବିଶ୍ୱବିଦ୍ୟାଳୟର ପ୍ରଫେସର | ତାଙ୍କ କାର୍ଯ୍ୟରେ ପ୍ରାୟତ f ନାରୀବାଦୀ ଥିମ୍ ଅନ୍ତର୍ଭୁକ୍ତ, ଏବଂ ପଶ୍ଚିମ କାନାଡାର ସଂସ୍କୃତିକୁ ଚିତ୍ରଣ ଏବଂ ବିଶ୍ଳେଷଣ କରିଥାଏ |
ଆରିଥା ୱାନ୍ ହର୍କ: ଆରିଥା ଭାନ୍ ହର୍କ ,, ଜଣେ କାନାଡିୟ ଲେଖକ, ସମାଲୋଚକ, ସମ୍ପାଦକ, ଜନ ବୁଦ୍ଧିଜୀବୀ ଏବଂ ବିଶ୍ୱବିଦ୍ୟାଳୟର ପ୍ରଫେସର | ତାଙ୍କ କାର୍ଯ୍ୟରେ ପ୍ରାୟତ f ନାରୀବାଦୀ ଥିମ୍ ଅନ୍ତର୍ଭୁକ୍ତ, ଏବଂ ପଶ୍ଚିମ କାନାଡାର ସଂସ୍କୃତିକୁ ଚିତ୍ରଣ ଏବଂ ବିଶ୍ଳେଷଣ କରିଥାଏ |
ଆରିଥାଙ୍ଗ (ବିଧାନସଭା ନିର୍ବାଚନମଣ୍ଡଳୀ): ଭାରତର ଉତ୍ତର ପୂର୍ବ ରାଜ୍ୟ ସିକ୍କିମର 32 ଟି ବିଧାନସଭା ନିର୍ବାଚନମଣ୍ଡଳୀ ମଧ୍ୟରୁ ଆରିଥାଙ୍ଗ ଅନ୍ୟତମ। ଏହି ନିର୍ବାଚନମଣ୍ଡଳୀ ସିକ୍କିମ ଲୋକସଭା ନିର୍ବାଚନମଣ୍ଡଳୀ ଅଧୀନରେ ରହିଛି।
ଆରିଥମ୍ୟାନ୍ସି: ଆଧୁନିକ ସାଂଖ୍ୟିକ ଶବ୍ଦଗୁଡ଼ିକରେ, ଗାଣିତିକତା ହେଉଛି ଏକ ଶବ୍ଦ ବା ବାକ୍ୟାଂଶରେ ସାଂଖ୍ୟିକ ମୂଲ୍ୟ ନ୍ୟସ୍ତ କରିବା ଉପରେ ଆଧାର କରି ପ୍ରାଚୀନ ଗ୍ରୀକ୍ ଆଇସୋସେଫି କିମ୍ବା ହିବ୍ରୁ / ଆରାମିକ୍ ଜେମାଟ୍ରିଆର ସରଳୀକୃତ ସଂସ୍କରଣ ମାଧ୍ୟମରେ, ଲାଟିନ୍ ବର୍ଣ୍ଣମାଳା ସହିତ ଅନୁକୂଳ | ଆରିଥମ୍ୟାନ୍ସି କଲଦୀୟ, ପ୍ଲାଟୋନିଷ୍ଟ, ପାଇଥାଗୋରୀୟ ଏବଂ କବାବାଲା ସହିତ ଜଡିତ | ଯେତେବେଳେ ଜଣେ ବ୍ୟକ୍ତିଙ୍କ ନାମରେ ଗଣିତ ପ୍ରୟୋଗ କରାଯାଏ, ଏହା ଏକ ଅନୋମ୍ୟାନ୍ସିର ଏକ ରୂପ |
ଆରିଥମୋମାନିଆ: ଆରିଥମୋମାନିଆ ହେଉଛି ଏକ ମାନସିକ ବିକୃତି ଯାହା ଅବସେସିଭ୍ - ବାଧ୍ୟତାମୂଳକ ବ୍ୟାଧି (OCD) ର ଅଭିବ୍ୟକ୍ତି ଭାବରେ ଦେଖାଯାଇପାରେ | ଏହି ବ୍ୟାଧିରେ ପୀଡିତ ବ୍ୟକ୍ତିବିଶେଷଙ୍କର ନିଜ କାର୍ଯ୍ୟ କିମ୍ବା ବସ୍ତୁକୁ ନିଜ ଆଖପାଖରେ ଗଣନା କରିବାର ପ୍ରବଳ ଆବଶ୍ୟକତା ଅଛି |
ଆରିଥମ୍ୟାନ୍ସି: ଆଧୁନିକ ସାଂଖ୍ୟିକ ଶବ୍ଦଗୁଡ଼ିକରେ, ଗାଣିତିକତା ହେଉଛି ଏକ ଶବ୍ଦ ବା ବାକ୍ୟାଂଶରେ ସାଂଖ୍ୟିକ ମୂଲ୍ୟ ନ୍ୟସ୍ତ କରିବା ଉପରେ ଆଧାର କରି ପ୍ରାଚୀନ ଗ୍ରୀକ୍ ଆଇସୋସେଫି କିମ୍ବା ହିବ୍ରୁ / ଆରାମିକ୍ ଜେମାଟ୍ରିଆର ସରଳୀକୃତ ସଂସ୍କରଣ ମାଧ୍ୟମରେ, ଲାଟିନ୍ ବର୍ଣ୍ଣମାଳା ସହିତ ଅନୁକୂଳ | ଆରିଥମ୍ୟାନ୍ସି କଲଦୀୟ, ପ୍ଲାଟୋନିଷ୍ଟ, ପାଇଥାଗୋରୀୟ ଏବଂ କବାବାଲା ସହିତ ଜଡିତ | ଯେତେବେଳେ ଜଣେ ବ୍ୟକ୍ତିଙ୍କ ନାମରେ ଗଣିତ ପ୍ରୟୋଗ କରାଯାଏ, ଏହା ଏକ ଅନୋମ୍ୟାନ୍ସିର ଏକ ରୂପ |
ଗାଣିତିକ: ଆରିଥମେଟିକ୍ ହେଉଛି ଗଣିତର ଏକ ଶାଖା ଯାହା ସଂଖ୍ୟାଗୁଡ଼ିକର ଅଧ୍ୟୟନକୁ ନେଇ ଗଠିତ, ବିଶେଷତ them ସେମାନଙ୍କ ଉପରେ ପାରମ୍ପାରିକ କାର୍ଯ୍ୟର ଗୁଣ - ଯୋଗ, ବିତରଣ, ଗୁଣନ, ବିଭାଜନ, ମୂଳ ଏବଂ ନିର୍ବାହ | ଆରିଥମେଟିକ୍ ହେଉଛି ସଂଖ୍ୟା ତତ୍ତ୍ an ର ଏକ ପ୍ରାଥମିକ ଅଂଶ, ଏବଂ ସଂଖ୍ୟା ଥିଓରୀକୁ ଆଧୁନିକ ଗଣିତର ଏକ ଉଚ୍ଚ ସ୍ତରୀୟ ବିଭାଗ ଭାବରେ ବିବେଚନା କରାଯାଏ, ବୀଜ୍, ଜ୍ୟାମିତି ଏବଂ ବିଶ୍ଳେଷଣ ସହିତ | ଆରିଥମେଟିକ୍ ଏବଂ ଉଚ୍ଚ ଆରିଥମେଟିକ୍ ଶବ୍ଦଗୁଡିକ ବିଂଶ ଶତାବ୍ଦୀର ଆରମ୍ଭ ପର୍ଯ୍ୟନ୍ତ ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତର ସମକକ୍ଷ ଭାବରେ ବ୍ୟବହୃତ ହୋଇଥିଲା ଏବଂ ବେଳେବେଳେ ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତର ଏକ ବ୍ୟାପକ ଅଂଶକୁ ସୂଚାଇବା ପାଇଁ ବ୍ୟବହୃତ ହୁଏ |
ଆଲଗୋରିଦମିକ୍ କାରବାର: ଆଲଗୋରିଦମିକ୍ ବାଣିଜ୍ୟ ହେଉଛି ସ୍ୱୟଂଚାଳିତ ପ୍ରି-ପ୍ରୋଗ୍ରାମ ହୋଇଥିବା ବାଣିଜ୍ୟ ନିର୍ଦ୍ଦେଶାବଳୀ ବ୍ୟବହାର କରି ଅର୍ଡର କାର୍ଯ୍ୟକାରୀ କରିବାର ଏକ ପଦ୍ଧତି, ଯେପରିକି ସମୟ, ମୂଲ୍ୟ, ଏବଂ ପରିମାଣ ପରି ଭେରିଏବଲ୍ ପାଇଁ ହିସାବ କରେ | ଏହି ପ୍ରକାର ବାଣିଜ୍ୟ ମାନବ ବ୍ୟବସାୟୀଙ୍କ ତୁଳନାରେ କମ୍ପ୍ୟୁଟରର ଗତି ଏବଂ ଗଣନାକାରୀ ଉତ୍ସକୁ ଉପଯୋଗ କରିବାକୁ ଚେଷ୍ଟା କରେ | ଏକବିଂଶ ଶତାବ୍ଦୀରେ ଆଲଗୋରିଦମିକ୍ କାରବାର ଉଭୟ ଖୁଚୁରା ଏବଂ ଅନୁଷ୍ଠାନିକ ବ୍ୟବସାୟୀଙ୍କ ସହ ଆକର୍ଷିତ ହୋଇପାରିଛି। ଏହା ପୁଞ୍ଜି ବିନିଯୋଗ ବ୍ୟାଙ୍କ, ପେନ୍ସନ୍ ପାଣ୍ଠି, ମ୍ୟୁଚୁଆଲ୍ ଫଣ୍ଡ ଏବଂ ହେଜ୍ ପାଣ୍ଠି ଦ୍ widely ାରା ବହୁଳ ଭାବରେ ବ୍ୟବହୃତ ହୁଏ ଯାହା ଏକ ବୃହତ ଆଦେଶର କାର୍ଯ୍ୟକାରିତା ବିସ୍ତାର କରିବାକୁ କିମ୍ବା ମାନବ ବ୍ୟବସାୟୀମାନଙ୍କ ପ୍ରତିକ୍ରିୟା ପାଇଁ ଅତି ଶୀଘ୍ର ବ୍ୟବସାୟ କରିବାକୁ ଆବଶ୍ୟକ କରିପାରନ୍ତି | 2019 ରେ ହୋଇଥିବା ଏକ ଅଧ୍ୟୟନରୁ ଜଣାପଡିଛି ଯେ ଫୋରେକ୍ସ ବଜାରରେ ପ୍ରାୟ 92% ବାଣିଜ୍ୟ ମଣିଷ ଅପେକ୍ଷା ବାଣିଜ୍ୟ ଆଲଗୋରିଦମ ଦ୍ୱାରା କରାଯାଇଥିଲା।
ଗାଣିତିକ ପ୍ରଗତି: ଏକ ଆରିଥମେଟିକ୍ ପ୍ରଗତି (AP) ବା ଗାଣିତିକ କ୍ରମ ହେଉଛି ସଂଖ୍ୟାଗୁଡ଼ିକର କ୍ରମ ଯେପରି କ୍ରମାଗତ ଶବ୍ଦଗୁଡ଼ିକ ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ ସ୍ଥିର ଅଟେ | ଉଦାହରଣ ସ୍ୱରୂପ, କ୍ରମ 5, 7, 9, 11, 13, 15 ,। 2 ର ସାଧାରଣ ପାର୍ଥକ୍ୟ ସହିତ ଏକ ଗାଣିତିକ ପ୍ରଗତି |
ଗାଣିତିକ ପ୍ରଗତି: ଏକ ଆରିଥମେଟିକ୍ ପ୍ରଗତି (AP) ବା ଗାଣିତିକ କ୍ରମ ହେଉଛି ସଂଖ୍ୟାଗୁଡ଼ିକର କ୍ରମ ଯେପରି କ୍ରମାଗତ ଶବ୍ଦଗୁଡ଼ିକ ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ ସ୍ଥିର ଅଟେ | ଉଦାହରଣ ସ୍ୱରୂପ, କ୍ରମ 5, 7, 9, 11, 13, 15 ,। 2 ର ସାଧାରଣ ପାର୍ଥକ୍ୟ ସହିତ ଏକ ଗାଣିତିକ ପ୍ରଗତି |
ଆରିଥମାଉରେଲ୍: ଆରିଥମାଉରେଲ୍ ଏକ ଯାନ୍ତ୍ରିକ କାଲକୁଲେଟର ଥିଲା ଯେଉଁଥିରେ ଏକ ଅତ୍ୟନ୍ତ ଅନ୍ତର୍ନିହିତ ଉପଭୋକ୍ତା ଇଣ୍ଟରଫେସ୍ ଥିଲା, ବିଶେଷତ numbers ସଂଖ୍ୟାକୁ ବହୁଗୁଣ ଏବଂ ବିଭାଜନ କରିବା ପାଇଁ କାରଣ ଅପରେଣ୍ଡସ୍ ପ୍ରବେଶ ହେବା ମାତ୍ରେ ଫଳାଫଳ ପ୍ରଦର୍ଶିତ ହୋଇଥିଲା | ଏହା ପ୍ରଥମେ ୧ 4242 ୨ ମସିହାରେ ଟିମୋଲେନ୍ ମ ure ରେଲଙ୍କ ଦ୍ France ାରା ଫ୍ରାନ୍ସରେ ପେଟେଣ୍ଟ ହୋଇଥିଲା। 1849 ମସିହାରେ ପ୍ୟାରିସରେ ଅନୁଷ୍ଠିତ ଫ୍ରାନ୍ସର ଜାତୀୟ ଶୋ'ରେ ଏହା ଏକ ସ୍ୱର୍ଣ୍ଣ ପଦକ ପାଇଥିଲା।
ଗାଣିତିକ: ଆରିଥମେଟିକ୍ ହେଉଛି ଗଣିତର ଏକ ଶାଖା ଯାହା ସଂଖ୍ୟାଗୁଡ଼ିକର ଅଧ୍ୟୟନକୁ ନେଇ ଗଠିତ, ବିଶେଷତ them ସେମାନଙ୍କ ଉପରେ ପାରମ୍ପାରିକ କାର୍ଯ୍ୟର ଗୁଣ - ଯୋଗ, ବିତରଣ, ଗୁଣନ, ବିଭାଜନ, ମୂଳ ଏବଂ ନିର୍ବାହ | ଆରିଥମେଟିକ୍ ହେଉଛି ସଂଖ୍ୟା ତତ୍ତ୍ an ର ଏକ ପ୍ରାଥମିକ ଅଂଶ, ଏବଂ ସଂଖ୍ୟା ଥିଓରୀକୁ ଆଧୁନିକ ଗଣିତର ଏକ ଉଚ୍ଚ ସ୍ତରୀୟ ବିଭାଗ ଭାବରେ ବିବେଚନା କରାଯାଏ, ବୀଜ୍, ଜ୍ୟାମିତି ଏବଂ ବିଶ୍ଳେଷଣ ସହିତ | ଆରିଥମେଟିକ୍ ଏବଂ ଉଚ୍ଚ ଆରିଥମେଟିକ୍ ଶବ୍ଦଗୁଡିକ ବିଂଶ ଶତାବ୍ଦୀର ଆରମ୍ଭ ପର୍ଯ୍ୟନ୍ତ ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତର ସମକକ୍ଷ ଭାବରେ ବ୍ୟବହୃତ ହୋଇଥିଲା ଏବଂ ବେଳେବେଳେ ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତର ଏକ ବ୍ୟାପକ ଅଂଶକୁ ସୂଚାଇବା ପାଇଁ ବ୍ୟବହୃତ ହୁଏ |
ଗାଣିତିକ - ଜ୍ୟାମିତିକ ଅର୍ଥ: ଗଣିତରେ, ଦୁଇଟି ସକାରାତ୍ମକ ପ୍ରକୃତ ସଂଖ୍ୟା x ଏବଂ y ର ଗାଣିତିକ - ଜ୍ୟାମିତିକ ଅର୍ଥ ( AGM ) କୁ ନିମ୍ନଲିଖିତ ଭାବରେ ବ୍ୟାଖ୍ୟା କରାଯାଇଛି:
ଗାଣିତିକ ଏବଂ ଜ୍ୟାମିତିକ ଅର୍ଥର ଅସମାନତା: ଗଣିତରେ, ଗାଣିତିକ ଏବଂ ଜ୍ୟାମିତିକ ଅର୍ଥର ଅସମାନତା , କିମ୍ବା ଅଧିକ ସଂକ୍ଷେପରେ AM - GM ଅସମାନତା ଦର୍ଶାଏ ଯେ ଅଣ-ନକାରାତ୍ମକ ପ୍ରକୃତ ସଂଖ୍ୟାର ତାଲିକାର ଗାଣିତିକ ଅର୍ଥ ସମାନ ତାଲିକାର ଜ୍ୟାମିତିକ ଅର୍ଥଠାରୁ ଅଧିକ କିମ୍ବା ସମାନ; ଏବଂ ଆହୁରି ମଧ୍ୟ, ଯଦି ତାଲିକାର ପ୍ରତ୍ୟେକ ସଂଖ୍ୟା ସମାନ ତେବେ ଦୁଇଟି ଅର୍ଥ ସମାନ |
ଗାଣିତିକ - ଜ୍ୟାମିତିକ ଅର୍ଥ: ଗଣିତରେ, ଦୁଇଟି ସକାରାତ୍ମକ ପ୍ରକୃତ ସଂଖ୍ୟା x ଏବଂ y ର ଗାଣିତିକ - ଜ୍ୟାମିତିକ ଅର୍ଥ ( AGM ) କୁ ନିମ୍ନଲିଖିତ ଭାବରେ ବ୍ୟାଖ୍ୟା କରାଯାଇଛି:
ଜ୍ୟାମିତିକ ଅର୍ଥ: ଗଣିତରେ, ଜ୍ୟାମିତିକ ଅର୍ଥ ହେଉଛି ଏକ ହାରାହାରି ବା ହାରାହାରି, ଯାହା ସେମାନଙ୍କର ମୂଲ୍ୟର ଉତ୍ପାଦ ବ୍ୟବହାର କରି ସଂଖ୍ୟାଗୁଡ଼ିକର ଏକ ସେଟ୍ ର କେନ୍ଦ୍ରୀୟ ପ୍ରବୃତ୍ତି କିମ୍ବା ସାଧାରଣ ମୂଲ୍ୟକୁ ସୂଚିତ କରେ | ଜ୍ୟାମିତିକ ଅର୍ଥ n ସଂଖ୍ୟାର ଉତ୍ପାଦର n th ମୂଳ ଭାବରେ ବ୍ୟାଖ୍ୟା କରାଯାଇଛି, ଅର୍ଥାତ୍ x 1 , x 2 , ..., x n ସଂଖ୍ୟାଗୁଡ଼ିକର ଏକ ସେଟ୍ ପାଇଁ, ଜ୍ୟାମିତିକ ଅର୍ଥ ପରି ବ୍ୟାଖ୍ୟା କରାଯାଇଛି |
ଲୋଗାରିଥମିକ୍ ଅର୍ଥ: ଗଣିତରେ, ଲୋଗାରିଥମିକ୍ ଅର୍ଥ ହେଉଛି ଦୁଇଟି ଅଣ-ନକାରାତ୍ମକ ସଂଖ୍ୟାର କାର୍ଯ୍ୟ, ଯାହା ସେମାନଙ୍କ ପାର୍ଥକ୍ୟର ଲୋଗାରିଦମ ଦ୍ divided ାରା ବିଭାଜିତ ପାର୍ଥକ୍ୟ ସହିତ ସମାନ | ଉତ୍ତାପ ଏବଂ ଜନ ସ୍ଥାନାନ୍ତରଣ ସହିତ ଜଡିତ ଇଞ୍ଜିନିୟରିଂ ସମସ୍ୟାରେ ଏହି ଗଣନା ପ୍ରଯୁଜ୍ୟ |
ଗାଣିତିକ ତର୍କ ଏକକ: ଗଣନାରେ, ଏକ ଆରିଥମେଟିକ୍ ଲଜିକ୍ ୟୁନିଟ୍ (ALU) ହେଉଛି ଏକ ମିଳିତ ଡିଜିଟାଲ୍ ସର୍କିଟ୍ ଯାହା ଇଣ୍ଟିଜର୍ ବାଇନାରୀ ନମ୍ବର ଉପରେ ଗାଣିତିକ ଏବଂ ବିଟୱାଇସ୍ ଅପରେସନ୍ କରିଥାଏ | ଏହା ଏକ ଫ୍ଲୋଟିଂ ପଏଣ୍ଟ ୟୁନିଟ୍ (FPU) ର ବିପରୀତ, ଯାହା ଫ୍ଲୋଟିଂ ପଏଣ୍ଟ ନମ୍ବର ଉପରେ କାର୍ଯ୍ୟ କରେ | ଏହା କମ୍ପ୍ୟୁଟର, FPU ଏବଂ ଗ୍ରାଫିକ୍ସ ପ୍ରକ୍ରିୟାକରଣ ୟୁନିଟ୍ (ଜିପିୟୁ) ର କେନ୍ଦ୍ରୀୟ ପ୍ରକ୍ରିୟାକରଣ ୟୁନିଟ୍ (CPU) ଅନ୍ତର୍ଭୂକ୍ତ କରି ଅନେକ ପ୍ରକାରର ଗଣନା ସର୍କିଟ୍ ର ଏକ ମ fundamental ଳିକ ବିଲ୍ଡିଂ ବ୍ଲକ୍ |
ଗାଣିତିକ (ଗୀତ): "ଗାଣିତିକ" Brooke Fraser ଦ୍ବାରା ଗୋଟିଏ ମାତ୍ର 2004 ଗୀତ ମୁକ୍ତିଲାଭ କରିବାକୁ Fraser ର ଜୀବନ ଆରମ୍ଭ ଆଲବମ୍ କ'ଣ ଦିବାଲୋକ ସହିତ ପ୍ରଥମ ଟ୍ରାକ୍ ହେଉଛି। ପରେ ଏହି ଗୀତଟି ସୋନି ବିଏମଜି ସଂକଳନ ମୋର୍ ପ୍ରକୃତି , ନ୍ୟୁଜିଲ୍ୟାଣ୍ଡ ସୋନି ବିଏମଜି କାଟାଲଗ୍ ର ଗୀତ ସଂଗ୍ରହରେ ଅନ୍ତର୍ଭୁକ୍ତ କରାଯାଇଥିଲା |
ଗାଣିତିକ (ଗୀତ): "ଗାଣିତିକ" Brooke Fraser ଦ୍ବାରା ଗୋଟିଏ ମାତ୍ର 2004 ଗୀତ ମୁକ୍ତିଲାଭ କରିବାକୁ Fraser ର ଜୀବନ ଆରମ୍ଭ ଆଲବମ୍ କ'ଣ ଦିବାଲୋକ ସହିତ ପ୍ରଥମ ଟ୍ରାକ୍ ହେଉଛି। ପରେ ଏହି ଗୀତଟି ସୋନି ବିଏମଜି ସଂକଳନ ମୋର୍ ପ୍ରକୃତି , ନ୍ୟୁଜିଲ୍ୟାଣ୍ଡ ସୋନି ବିଏମଜି କାଟାଲଗ୍ ର ଗୀତ ସଂଗ୍ରହରେ ଅନ୍ତର୍ଭୁକ୍ତ କରାଯାଇଥିଲା |
ଗାଣିତିକ ତର୍କ ଏକକ: ଗଣନାରେ, ଏକ ଆରିଥମେଟିକ୍ ଲଜିକ୍ ୟୁନିଟ୍ (ALU) ହେଉଛି ଏକ ମିଳିତ ଡିଜିଟାଲ୍ ସର୍କିଟ୍ ଯାହା ଇଣ୍ଟିଜର୍ ବାଇନାରୀ ନମ୍ବର ଉପରେ ଗାଣିତିକ ଏବଂ ବିଟୱାଇସ୍ ଅପରେସନ୍ କରିଥାଏ | ଏହା ଏକ ଫ୍ଲୋଟିଂ ପଏଣ୍ଟ ୟୁନିଟ୍ (FPU) ର ବିପରୀତ, ଯାହା ଫ୍ଲୋଟିଂ ପଏଣ୍ଟ ନମ୍ବର ଉପରେ କାର୍ଯ୍ୟ କରେ | ଏହା କମ୍ପ୍ୟୁଟର, FPU ଏବଂ ଗ୍ରାଫିକ୍ସ ପ୍ରକ୍ରିୟାକରଣ ୟୁନିଟ୍ (ଜିପିୟୁ) ର କେନ୍ଦ୍ରୀୟ ପ୍ରକ୍ରିୟାକରଣ ୟୁନିଟ୍ (CPU) ଅନ୍ତର୍ଭୂକ୍ତ କରି ଅନେକ ପ୍ରକାରର ଗଣନା ସର୍କିଟ୍ ର ଏକ ମ fundamental ଳିକ ବିଲ୍ଡିଂ ବ୍ଲକ୍ |
ଗାଣିତିକ ଜ୍ୟାମିତି: ଗଣିତରେ, ଗାଣିତିକ ଜ୍ୟାମିତି ପ୍ରାୟତ al ବୀଜ ବର୍ଣ୍ଣିତ ଜ୍ୟାମିତିରୁ ସଂଖ୍ୟା ତତ୍ତ୍ problems ର ସମସ୍ୟା ପର୍ଯ୍ୟନ୍ତ କ techni ଶଳର ପ୍ରୟୋଗ ଅଟେ | ଆରିଥମେଟିକ୍ ଜ୍ୟାମିତ୍ରୀ ଡାୟୋଫାଣ୍ଟାଇନ୍ ଜ୍ୟାମିତିର ଚାରିପାଖରେ କେନ୍ଦ୍ରୀଭୂତ ହୋଇଛି, ବୀଜ ବର୍ଣ୍ଣିତ କିସମର ଯୁକ୍ତିଯୁକ୍ତ ବିନ୍ଦୁ ଅଧ୍ୟୟନ |
ଆରାକେଲୋଭ୍ ସିଦ୍ଧାନ୍ତ: ଗଣିତରେ, ଆରାକେଲୋଭ୍ ସିଦ୍ଧାନ୍ତ ହେଉଛି ଡାଇଓଫାଣ୍ଟାଇନ୍ ଜ୍ୟାମିତିର ଏକ ଆଭିମୁଖ୍ୟ, ଯାହା ସୁରେନ୍ ଆରାକେଲୋଭ୍ ପାଇଁ ନାମିତ | ଉଚ୍ଚ ଆକାରରେ ଡାଇଓଫାଣ୍ଟାଇନ୍ ସମୀକରଣ ଅଧ୍ୟୟନ ପାଇଁ ଏହା ବ୍ୟବହୃତ ହୁଏ |
ଗାଣିତିକ କୋଡିଂ: ଆରିଥମେଟିକ୍ କୋଡିଂ ହେଉଛି କ୍ଷତିହୀନ ଡାଟା ସଙ୍କୋଚନରେ ବ୍ୟବହୃତ ଏଣ୍ଟ୍ରପି ଏନକୋଡିଂର ଏକ ରୂପ | ସାଧାରଣତ ,, ASCII କୋଡ୍ ପରି ଅକ୍ଷରଗୁଡିକର ଏକ ଷ୍ଟ୍ରିଙ୍ଗ୍ ଯେପରିକି "ହେଲୋ ସେଠାରେ" ଶବ୍ଦଗୁଡିକ ପ୍ରତି ଅକ୍ଷର ପ୍ରତି ନିର୍ଦ୍ଦିଷ୍ଟ ସଂଖ୍ୟକ ବିଟ୍ ବ୍ୟବହାର କରି ଉପସ୍ଥାପିତ ହୁଏ | ଯେତେବେଳେ ଏକ ଷ୍ଟ୍ରିଙ୍ଗ୍ ଆରିଥମେଟିକ୍ ଏନକୋଡିଂରେ ରୂପାନ୍ତରିତ ହୁଏ, ବାରମ୍ବାର ବ୍ୟବହୃତ ଅକ୍ଷରଗୁଡ଼ିକ କମ୍ ବିଟ୍ ସହିତ ଗଚ୍ଛିତ ହେବ ଏବଂ ବାରମ୍ବାର ଘଟୁଥିବା ଅକ୍ଷରଗୁଡିକ ଅଧିକ ବିଟ୍ ସହିତ ଗଚ୍ଛିତ ହେବ, ଫଳସ୍ୱରୂପ ସମୁଦାୟ ବ୍ୟବହୃତ କମ୍ ବିଟ୍ | ଆରିଥମେଟିକ୍ କୋଡିଂ ଅନ୍ୟ ପ୍ରକାର ଏଣ୍ଟ୍ରପି ଏନକୋଡିଂ ଠାରୁ ଭିନ୍ନ, ଯେପରିକି ହଫମାନ କୋଡିଂ, ଏଥିରେ ଇନପୁଟକୁ ଉପାଦାନ ସଙ୍କେତରେ ପୃଥକ କରିବା ଏବଂ ପ୍ରତ୍ୟେକକୁ ଏକ କୋଡ୍ ସହିତ ବଦଳାଇବା ପରିବର୍ତ୍ତେ, ଆରିଥମେଟିକ୍ କୋଡିଂ ସମଗ୍ର ସନ୍ଦେଶକୁ ଏକ ନମ୍ବରରେ ଏନକୋଡ୍ କରେ, ଏକ ଇଚ୍ଛାଧୀନ-ସଠିକତା ଭଗ୍ନାଂଶ q ଯେଉଁଠାରେ 0.0 ≤ q <1.0। ଏହା ସାମ୍ପ୍ରତିକ ସୂଚନାକୁ ଏକ ପରିସର ଭାବରେ ଦର୍ଶାଏ, ଦୁଇଟି ସଂଖ୍ୟା ଦ୍ୱାରା ବ୍ୟାଖ୍ୟା କରାଯାଇଛି | ଅସୀମେଟ୍ରିକ୍ ସାଂଖ୍ୟିକ ପ୍ରଣାଳୀ ନାମକ ଏକ ଏଣ୍ଟ୍ରପି କୋଡର୍ ର ଏକ ପରିବାର ବର୍ତ୍ତମାନର ସୂଚନାକୁ ପ୍ରତିନିଧିତ୍ୱ କରୁଥିବା ଏକ ପ୍ରାକୃତିକ ସଂଖ୍ୟାରେ ସିଧାସଳଖ କାର୍ଯ୍ୟ କରିଥିବାରୁ ଶୀଘ୍ର କାର୍ଯ୍ୟକାରିତା ପାଇଁ ଅନୁମତି ଦେଇଥାଏ |
ଗାଣିତିକ ଏବଂ ଜ୍ୟାମିତିକ ଫ୍ରୋବେନିୟସ୍: ଗଣିତ, Frobenius endomorphism କୌଣସି commutative ବୃତ୍ତ R ଯାହା କରିବା ସ୍ବଭାବ p ଯେଉଁଠି p ଏକ ପ୍ରଧାନମନ୍ତ୍ରୀ ସଂଖ୍ଯା ଅଟେ, ବ୍ୟାଖ୍ୟା ହୋଇଛି। ୟିଖରିଯ, ମ୍ୟାପିଂ φ ଯାହା R p କୁ R ରେ R ନିଏ R ର ଏକ ବୃତ୍ତ endomorphism ଅଟେ।
ଫ୍ରୋବେନିୟସ୍ ଏଣ୍ଡୋମର୍ଫିଜିମ୍: କମ୍ୟୁଟେଟିଭ୍ ଆଲଜେବ୍ରା ଏବଂ ଫିଲ୍ଡ ସିଦ୍ଧାନ୍ତରେ, ଫ୍ରୋବେନିୟସ୍ ଏଣ୍ଡୋମୋର୍ଫିଜିମ୍ ହେଉଛି ପ୍ରାଇମେଟିକ୍ ଚରିତ୍ରିକ p ସହିତ କମ୍ୟୁଟିଭ୍ ରିଙ୍ଗର ଏକ ସ୍ୱତନ୍ତ୍ର ଏଣ୍ଡୋମର୍ଫିଜିମ୍, ଏକ ଗୁରୁତ୍ୱପୂର୍ଣ୍ଣ ଶ୍ରେଣୀ ଯେଉଁଥିରେ ସୀମିତ କ୍ଷେତ୍ର ଅନ୍ତର୍ଭୁକ୍ତ | ଏଣ୍ଡୋମର୍ଫିଜିମ୍ ପ୍ରତ୍ୟେକ ଉପାଦାନକୁ ଏହାର p- ଶକ୍ତି ସହିତ ମାନଚିତ୍ର କରେ | ନିର୍ଦ୍ଦିଷ୍ଟ ପ୍ରସଙ୍ଗରେ ଏହା ଏକ ଅଟୋମୋର୍ଫିଜିମ୍, କିନ୍ତୁ ସାଧାରଣତ this ଏହା ସତ୍ୟ ନୁହେଁ |
ଗାଣିତିକ ଫୁଚିଆନ୍ ଗୋଷ୍ଠୀ: ଆରିଥମେଟିକ୍ ଫୁଚିଆନ୍ ଗୋଷ୍ଠୀଗୁଡ଼ିକ ହେଉଛି କ୍ୱାଟର୍ନିଅନ୍ ଆଲଜେବ୍ରାରେ ଅର୍ଡର ବ୍ୟବହାର କରି ନିର୍ମିତ ଫୁଚିଆନ୍ ଗୋଷ୍ଠୀର ଏକ ସ୍ୱତନ୍ତ୍ର ଶ୍ରେଣୀ | ସେମାନେ ଗାଣିତିକ ଗୋଷ୍ଠୀର ନିର୍ଦ୍ଦିଷ୍ଟ ଉଦାହରଣ | ଏକ ଗାଣିତିକ ଫୁଚିଆନ୍ ଗୋଷ୍ଠୀର ପ୍ରୋଟୋଟାଇପିକାଲ୍ ଉଦାହରଣ ହେଉଛି ମଡ୍ୟୁଲାର୍ ଗ୍ରୁପ୍ | । ସେମାନେ, ଏବଂ ହାଇପରବୋଲିକ୍ ପୃଷ୍ଠରେ ସେମାନଙ୍କର କାର୍ଯ୍ୟ ସହିତ ଜଡିତ ହାଇପରବୋଲିକ୍ ପୃଷ୍ଠ ପ୍ରାୟତ Fu ଫୁଚିଆନ୍ ଗୋଷ୍ଠୀ ଏବଂ ହାଇପରବୋଲିକ୍ ପୃଷ୍ଠଗୁଡ଼ିକ ମଧ୍ୟରେ ନିୟମିତ ଆଚରଣ ପ୍ରଦର୍ଶନ କରେ |
ଡାଇଓଫାଣ୍ଟାଇନ୍ ସମୀକରଣ: ଗଣିତରେ, ଏକ ଡାଇଓଫାଣ୍ଟାଇନ୍ ସମୀକରଣ ହେଉଛି ଏକ ବହୁଭୂତ ସମୀକରଣ, ସାଧାରଣତ two ଦୁଇ କିମ୍ବା ଅଧିକ ଅଜ୍ଞାତ ସହିତ ଜଡିତ, ଯେପରି ଆଗ୍ରହର ଏକମାତ୍ର ସମାଧାନ ହେଉଛି ପୂର୍ଣ୍ଣ ସଂଖ୍ୟା | ଏକ ର line ଖ୍ୟ ଡାୟୋଫାଣ୍ଟାଇନ୍ ସମୀକରଣ ଏକ ସ୍ଥିର ଦୁଇ କିମ୍ବା ଅଧିକ ମୋନୋମିଆଲ୍ ର ସମଷ୍ଟି ସହିତ ସମାନ, ପ୍ରତ୍ୟେକ ଡିଗ୍ରୀ ଏକ | ଏକ ଏକ୍ସପୋନ୍ସେନାଲ୍ ଡାୟୋଫାଣ୍ଟାଇନ୍ ସମୀକରଣ ହେଉଛି ଯେଉଁଥିରେ ଅଜ୍ଞାତମାନେ ଏକ୍ସପୋଜର୍ରେ ଦେଖାଯିବେ |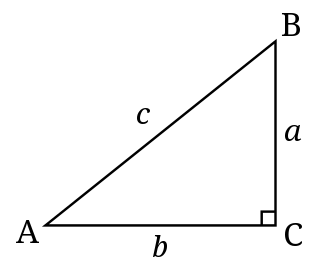
ଗାଣିତିକ IF: ଆରିଥମେଟିକ୍ IF ଷ୍ଟେଟମେଣ୍ଟ ହେଉଛି ଏକ ତିନି-ମାର୍ଗ ଗଣିତ କଣ୍ଡିଶନାଲ୍ ଷ୍ଟେଟମେଣ୍ଟ, ପ୍ରଥମେ 1957 ରେ ଫୋର୍ଟ୍ରାନ୍ ର ପ୍ରଥମ ପ୍ରକାଶନରେ ଦେଖାଯାଇଥିଲା ଏବଂ ପରବର୍ତ୍ତୀ ସଂସ୍କରଣରେ ଏବଂ ଅନ୍ୟାନ୍ୟ ପ୍ରୋଗ୍ରାମିଂ ଭାଷା ଯେପରିକି FOCAL | ଅନ୍ୟ ଭାଷାରେ ଦେଖାଯାଇଥିବା ଯୁକ୍ତିଯୁକ୍ତ IF ଷ୍ଟେଟମେଣ୍ଟ ପରି, ଫୋର୍ଟ୍ରାନ୍ ଷ୍ଟେଟମେଣ୍ଟ୍ ତିନୋଟି ଭିନ୍ନ ଶାଖାକୁ ବ୍ୟାଖ୍ୟା କରେ ଯାହା ଉପରେ ନିର୍ଭର କରି ଏକ ଅଭିବ୍ୟକ୍ତିର ଫଳାଫଳ ନକାରାତ୍ମକ, ଶୂନ୍ୟ କିମ୍ବା ସକରାତ୍ମକ ଅଟେ:
ଗାଣିତିକ ହାଇପରବୋଲିକ୍ 3-ଗୁଣ: ଗଣିତରେ, ସଠିକ୍ ଭାବରେ ଗୋଷ୍ଠୀ ସିଦ୍ଧାନ୍ତ ଏବଂ ହାଇପରବୋଲିକ୍ ଜ୍ୟାମିତ୍ରୀରେ , ଆରିଥମେଟିକ୍ କ୍ଲିନିଆନ୍ ଗୋଷ୍ଠୀଗୁଡିକ କ୍ୱାଟର୍ନିଅନ୍ ବୀଜ ବର୍ଣ୍ଣରେ ଅର୍ଡର ବ୍ୟବହାର କରି ନିର୍ମିତ କ୍ଲିନିଆନ୍ ଗୋଷ୍ଠୀର ଏକ ସ୍ୱତନ୍ତ୍ର ଶ୍ରେଣୀ | ସେମାନେ ଗାଣିତିକ ଗୋଷ୍ଠୀର ନିର୍ଦ୍ଦିଷ୍ଟ ଉଦାହରଣ | ଏକ ଆରିଥମେଟିକ୍ ହାଇପରବୋଲିକ୍ ଥ୍ରୀ-ମେନିଫୋଲ୍ଡ ହେଉଛି ହାଇପରବୋଲିକ୍ ସ୍ପେସ୍ ର କୋଟୋଏଣ୍ଟ୍ | ଏକ ଗାଣିତିକ କ୍ଲିନିଆନ୍ ଗୋଷ୍ଠୀ ଦ୍ୱାରା | ଏହି ମେନିଫୋଲ୍ଡଗୁଡ଼ିକରେ କିଛି ବିଶେଷ ସୁନ୍ଦର ବା ଉଲ୍ଲେଖନୀୟ ଉଦାହରଣ ଅନ୍ତର୍ଭୁକ୍ତ |
ଗାଣିତିକ ତର୍କ ଏକକ: ଗଣନାରେ, ଏକ ଆରିଥମେଟିକ୍ ଲଜିକ୍ ୟୁନିଟ୍ (ALU) ହେଉଛି ଏକ ମିଳିତ ଡିଜିଟାଲ୍ ସର୍କିଟ୍ ଯାହା ଇଣ୍ଟିଜର୍ ବାଇନାରୀ ନମ୍ବର ଉପରେ ଗାଣିତିକ ଏବଂ ବିଟୱାଇସ୍ ଅପରେସନ୍ କରିଥାଏ | ଏହା ଏକ ଫ୍ଲୋଟିଂ ପଏଣ୍ଟ ୟୁନିଟ୍ (FPU) ର ବିପରୀତ, ଯାହା ଫ୍ଲୋଟିଂ ପଏଣ୍ଟ ନମ୍ବର ଉପରେ କାର୍ଯ୍ୟ କରେ | ଏହା କମ୍ପ୍ୟୁଟର, FPU ଏବଂ ଗ୍ରାଫିକ୍ସ ପ୍ରକ୍ରିୟାକରଣ ୟୁନିଟ୍ (ଜିପିୟୁ) ର କେନ୍ଦ୍ରୀୟ ପ୍ରକ୍ରିୟାକରଣ ୟୁନିଟ୍ (CPU) ଅନ୍ତର୍ଭୂକ୍ତ କରି ଅନେକ ପ୍ରକାରର ଗଣନା ସର୍କିଟ୍ ର ଏକ ମ fundamental ଳିକ ବିଲ୍ଡିଂ ବ୍ଲକ୍ |
ଗାଣିତିକ ଅର୍ଥ: ଗଣିତ ଏବଂ ପରିସଂଖ୍ୟାନରେ, ଗାଣିତିକ ଅର୍ଥ , କିମ୍ବା କେବଳ ଅର୍ଥ ବା ହାରାହାରି , ସଂଗ୍ରହରେ ସଂଖ୍ୟା ଗଣନା ଦ୍ୱାରା ବିଭକ୍ତ ସଂଖ୍ୟା ସଂଗ୍ରହର ସମଷ୍ଟି ଅଟେ | ସଂଗ୍ରହ ପ୍ରାୟତ an ଏକ ପରୀକ୍ଷଣ କିମ୍ବା ପର୍ଯ୍ୟବେକ୍ଷଣଶୀଳ ଅଧ୍ୟୟନର ଫଳାଫଳର ଏକ ସେଟ୍, କିମ୍ବା ବାରମ୍ବାର ଏକ ସର୍ବେକ୍ଷଣରୁ ଫଳାଫଳର ଏକ ସେଟ୍ | ଗଣିତ ଏବଂ ପରିସଂଖ୍ୟାନରେ କେତେକ ପ୍ରସଙ୍ଗରେ "ଗାଣିତିକ ଅର୍ଥ" ଶବ୍ଦକୁ ଅଧିକ ପସନ୍ଦ କରାଯାଏ, କାରଣ ଏହା ଏହାକୁ ଅନ୍ୟ ଉପାୟଠାରୁ ଭିନ୍ନ କରିବାରେ ସାହାଯ୍ୟ କରିଥାଏ, ଯେପରିକି ଜ୍ୟାମିତିକ ଅର୍ଥ ଏବଂ ହାରମୋନିକ୍ ଅର୍ଥ |
ଗାଣିତିକ ଏବଂ ଜ୍ୟାମିତିକ ଅର୍ଥର ଅସମାନତା: ଗଣିତରେ, ଗାଣିତିକ ଏବଂ ଜ୍ୟାମିତିକ ଅର୍ଥର ଅସମାନତା , କିମ୍ବା ଅଧିକ ସଂକ୍ଷେପରେ AM - GM ଅସମାନତା ଦର୍ଶାଏ ଯେ ଅଣ-ନକାରାତ୍ମକ ପ୍ରକୃତ ସଂଖ୍ୟାର ତାଲିକାର ଗାଣିତିକ ଅର୍ଥ ସମାନ ତାଲିକାର ଜ୍ୟାମିତିକ ଅର୍ଥଠାରୁ ଅଧିକ କିମ୍ବା ସମାନ; ଏବଂ ଆହୁରି ମଧ୍ୟ, ଯଦି ତାଲିକାର ପ୍ରତ୍ୟେକ ସଂଖ୍ୟା ସମାନ ତେବେ ଦୁଇଟି ଅର୍ଥ ସମାନ |
ଗାଣିତିକ ପ୍ରଗତି: ଏକ ଆରିଥମେଟିକ୍ ପ୍ରଗତି (AP) ବା ଗାଣିତିକ କ୍ରମ ହେଉଛି ସଂଖ୍ୟାଗୁଡ଼ିକର କ୍ରମ ଯେପରି କ୍ରମାଗତ ଶବ୍ଦଗୁଡ଼ିକ ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ ସ୍ଥିର ଅଟେ | ଉଦାହରଣ ସ୍ୱରୂପ, କ୍ରମ 5, 7, 9, 11, 13, 15 ,। 2 ର ସାଧାରଣ ପାର୍ଥକ୍ୟ ସହିତ ଏକ ଗାଣିତିକ ପ୍ରଗତି |
ଆରାକେଲୋଭ୍ ସିଦ୍ଧାନ୍ତ: ଗଣିତରେ, ଆରାକେଲୋଭ୍ ସିଦ୍ଧାନ୍ତ ହେଉଛି ଡାଇଓଫାଣ୍ଟାଇନ୍ ଜ୍ୟାମିତିର ଏକ ଆଭିମୁଖ୍ୟ, ଯାହା ସୁରେନ୍ ଆରାକେଲୋଭ୍ ପାଇଁ ନାମିତ | ଉଚ୍ଚ ଆକାରରେ ଡାଇଓଫାଣ୍ଟାଇନ୍ ସମୀକରଣ ଅଧ୍ୟୟନ ପାଇଁ ଏହା ବ୍ୟବହୃତ ହୁଏ |
ଆରାକେଲୋଭ୍ ସିଦ୍ଧାନ୍ତ: ଗଣିତରେ, ଆରାକେଲୋଭ୍ ସିଦ୍ଧାନ୍ତ ହେଉଛି ଡାଇଓଫାଣ୍ଟାଇନ୍ ଜ୍ୟାମିତିର ଏକ ଆଭିମୁଖ୍ୟ, ଯାହା ସୁରେନ୍ ଆରାକେଲୋଭ୍ ପାଇଁ ନାମିତ | ଉଚ୍ଚ ଆକାରରେ ଡାଇଓଫାଣ୍ଟାଇନ୍ ସମୀକରଣ ଅଧ୍ୟୟନ ପାଇଁ ଏହା ବ୍ୟବହୃତ ହୁଏ |
ଗାଣିତିକ ପ୍ରଗତି: ଏକ ଆରିଥମେଟିକ୍ ପ୍ରଗତି (AP) ବା ଗାଣିତିକ କ୍ରମ ହେଉଛି ସଂଖ୍ୟାଗୁଡ଼ିକର କ୍ରମ ଯେପରି କ୍ରମାଗତ ଶବ୍ଦଗୁଡ଼ିକ ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ ସ୍ଥିର ଅଟେ | ଉଦାହରଣ ସ୍ୱରୂପ, କ୍ରମ 5, 7, 9, 11, 13, 15 ,। 2 ର ସାଧାରଣ ପାର୍ଥକ୍ୟ ସହିତ ଏକ ଗାଣିତିକ ପ୍ରଗତି |
ଗାଣିତିକ ପୃଷ୍ଠ: ଗଣିତରେ, ଭଗ୍ନାଂଶ କ୍ଷେତ୍ର ସହିତ ଏକ ଡେଡେକିଣ୍ଡ ଡୋମେନ୍ R ଉପରେ ଏକ ଗଣିତ ପୃଷ୍ଠ | ଏକ ଜ୍ୟାମିତିକ ବସ୍ତୁ ହେଉଛି ଗୋଟିଏ ପାରମ୍ପାରିକ ଡାଇମେନ୍ସନ୍, ଏବଂ ଅନ୍ୟ ଏକ ଡାଇମେନ୍ସନ୍ ପ୍ରାଇମ୍ସର ଅସୀମତା ଦ୍ୱାରା ପ୍ରଦତ୍ତ | ଯେତେବେଳେ R ହେଉଛି ଇଣ୍ଟିଜର୍ Z ର ରିଙ୍ଗ, ଏହି ଅନ୍ତର୍ନିହିତତା ଏକ ଆଦର୍ଶ ସହିତ ଦେଖାଯାଉଥିବା ମୂଖ୍ୟ ଆଦର୍ଶ ସ୍ପେକ୍ଟ୍ରମ୍ ସ୍ପେକ୍ ( Z ) ଉପରେ ନିର୍ଭର କରେ | ଆରିଥମେଟିକ୍ ପୃଷ୍ଠଗୁଡ଼ିକ ଡାଇଓଫାଣ୍ଟାଇନ୍ ଜ୍ୟାମିତୀରେ ସ୍ natural ାଭାବିକ ଭାବରେ ଉତ୍ପନ୍ନ ହୁଏ, ଯେତେବେଳେ K ଉପରେ ବ୍ୟାଖ୍ୟା କରାଯାଇଥିବା ଏକ ବୀଜ ବର୍ଣ୍ଣିତ ବକ୍ର R / P କ୍ଷେତ୍ର ଉପରେ ହ୍ରାସ ବୋଲି ଚିନ୍ତା କରାଯାଏ, ଯେଉଁଠାରେ P R ର ଏକ ଆଦର୍ଶ ଅଟେ, ପ୍ରାୟ ସମସ୍ତ P ପାଇଁ ; ଏବଂ R / P କୁ ହ୍ରାସ କରିବାର ପ୍ରକ୍ରିୟା ବିଷୟରେ କ'ଣ ଘଟିବା ଉଚିତ ତାହା ନିର୍ଦ୍ଧିଷ୍ଟ କରିବାରେ ସହାୟକ ହୋଇଥାଏ ଯେତେବେଳେ ଅତ୍ୟନ୍ତ ନିର୍ବୋଧ ଉପାୟ ବୁ sense ିବାରେ ବିଫଳ ହୁଏ |
ଆଲଗୋରିଦମିକ୍ କାରବାର: ଆଲଗୋରିଦମିକ୍ ବାଣିଜ୍ୟ ହେଉଛି ସ୍ୱୟଂଚାଳିତ ପ୍ରି-ପ୍ରୋଗ୍ରାମ ହୋଇଥିବା ବାଣିଜ୍ୟ ନିର୍ଦ୍ଦେଶାବଳୀ ବ୍ୟବହାର କରି ଅର୍ଡର କାର୍ଯ୍ୟକାରୀ କରିବାର ଏକ ପଦ୍ଧତି, ଯେପରିକି ସମୟ, ମୂଲ୍ୟ, ଏବଂ ପରିମାଣ ପରି ଭେରିଏବଲ୍ ପାଇଁ ହିସାବ କରେ | ଏହି ପ୍ରକାର ବାଣିଜ୍ୟ ମାନବ ବ୍ୟବସାୟୀଙ୍କ ତୁଳନାରେ କମ୍ପ୍ୟୁଟରର ଗତି ଏବଂ ଗଣନାକାରୀ ଉତ୍ସକୁ ଉପଯୋଗ କରିବାକୁ ଚେଷ୍ଟା କରେ | ଏକବିଂଶ ଶତାବ୍ଦୀରେ ଆଲଗୋରିଦମିକ୍ କାରବାର ଉଭୟ ଖୁଚୁରା ଏବଂ ଅନୁଷ୍ଠାନିକ ବ୍ୟବସାୟୀଙ୍କ ସହ ଆକର୍ଷିତ ହୋଇପାରିଛି। ଏହା ପୁଞ୍ଜି ବିନିଯୋଗ ବ୍ୟାଙ୍କ, ପେନ୍ସନ୍ ପାଣ୍ଠି, ମ୍ୟୁଚୁଆଲ୍ ଫଣ୍ଡ ଏବଂ ହେଜ୍ ପାଣ୍ଠି ଦ୍ widely ାରା ବହୁଳ ଭାବରେ ବ୍ୟବହୃତ ହୁଏ ଯାହା ଏକ ବୃହତ ଆଦେଶର କାର୍ଯ୍ୟକାରିତା ବିସ୍ତାର କରିବାକୁ କିମ୍ବା ମାନବ ବ୍ୟବସାୟୀମାନଙ୍କ ପ୍ରତିକ୍ରିୟା ପାଇଁ ଅତି ଶୀଘ୍ର ବ୍ୟବସାୟ କରିବାକୁ ଆବଶ୍ୟକ କରିପାରନ୍ତି | 2019 ରେ ହୋଇଥିବା ଏକ ଅଧ୍ୟୟନରୁ ଜଣାପଡିଛି ଯେ ଫୋରେକ୍ସ ବଜାରରେ ପ୍ରାୟ 92% ବାଣିଜ୍ୟ ମଣିଷ ଅପେକ୍ଷା ବାଣିଜ୍ୟ ଆଲଗୋରିଦମ ଦ୍ୱାରା କରାଯାଇଥିଲା।
ଗାଣିତିକ ଜ୍ୟାମିତି: ଗଣିତରେ, ଗାଣିତିକ ଜ୍ୟାମିତି ପ୍ରାୟତ al ବୀଜ ବର୍ଣ୍ଣିତ ଜ୍ୟାମିତିରୁ ସଂଖ୍ୟା ତତ୍ତ୍ problems ର ସମସ୍ୟା ପର୍ଯ୍ୟନ୍ତ କ techni ଶଳର ପ୍ରୟୋଗ ଅଟେ | ଆରିଥମେଟିକ୍ ଜ୍ୟାମିତ୍ରୀ ଡାୟୋଫାଣ୍ଟାଇନ୍ ଜ୍ୟାମିତିର ଚାରିପାଖରେ କେନ୍ଦ୍ରୀଭୂତ ହୋଇଛି, ବୀଜ ବର୍ଣ୍ଣିତ କିସମର ଯୁକ୍ତିଯୁକ୍ତ ବିନ୍ଦୁ ଅଧ୍ୟୟନ |
ଗାଣିତିକ ତର୍କ ଏକକ: ଗଣନାରେ, ଏକ ଆରିଥମେଟିକ୍ ଲଜିକ୍ ୟୁନିଟ୍ (ALU) ହେଉଛି ଏକ ମିଳିତ ଡିଜିଟାଲ୍ ସର୍କିଟ୍ ଯାହା ଇଣ୍ଟିଜର୍ ବାଇନାରୀ ନମ୍ବର ଉପରେ ଗାଣିତିକ ଏବଂ ବିଟୱାଇସ୍ ଅପରେସନ୍ କରିଥାଏ | ଏହା ଏକ ଫ୍ଲୋଟିଂ ପଏଣ୍ଟ ୟୁନିଟ୍ (FPU) ର ବିପରୀତ, ଯାହା ଫ୍ଲୋଟିଂ ପଏଣ୍ଟ ନମ୍ବର ଉପରେ କାର୍ଯ୍ୟ କରେ | ଏହା କମ୍ପ୍ୟୁଟର, FPU ଏବଂ ଗ୍ରାଫିକ୍ସ ପ୍ରକ୍ରିୟାକରଣ ୟୁନିଟ୍ (ଜିପିୟୁ) ର କେନ୍ଦ୍ରୀୟ ପ୍ରକ୍ରିୟାକରଣ ୟୁନିଟ୍ (CPU) ଅନ୍ତର୍ଭୂକ୍ତ କରି ଅନେକ ପ୍ରକାରର ଗଣନା ସର୍କିଟ୍ ର ଏକ ମ fundamental ଳିକ ବିଲ୍ଡିଂ ବ୍ଲକ୍ |
ଗାଣିତିକ ଏବଂ ଜ୍ୟାମିତିକ ଫ୍ରୋବେନିୟସ୍: ଗଣିତ, Frobenius endomorphism କୌଣସି commutative ବୃତ୍ତ R ଯାହା କରିବା ସ୍ବଭାବ p ଯେଉଁଠି p ଏକ ପ୍ରଧାନମନ୍ତ୍ରୀ ସଂଖ୍ଯା ଅଟେ, ବ୍ୟାଖ୍ୟା ହୋଇଛି। ୟିଖରିଯ, ମ୍ୟାପିଂ φ ଯାହା R p କୁ R ରେ R ନିଏ R ର ଏକ ବୃତ୍ତ endomorphism ଅଟେ।
ଗାଣିତିକ ଏବଂ ଜ୍ୟାମିତିକ ଫ୍ରୋବେନିୟସ୍: ଗଣିତ, Frobenius endomorphism କୌଣସି commutative ବୃତ୍ତ R ଯାହା କରିବା ସ୍ବଭାବ p ଯେଉଁଠି p ଏକ ପ୍ରଧାନମନ୍ତ୍ରୀ ସଂଖ୍ଯା ଅଟେ, ବ୍ୟାଖ୍ୟା ହୋଇଛି। ୟିଖରିଯ, ମ୍ୟାପିଂ φ ଯାହା R p କୁ R ରେ R ନିଏ R ର ଏକ ବୃତ୍ତ endomorphism ଅଟେ।
ନିର୍ଦ୍ଦେଶ ସେଟ୍ ସ୍ଥାପତ୍ୟ: କମ୍ପ୍ୟୁଟର ବିଜ୍ଞାନରେ, ଏକ ନିର୍ଦ୍ଦେଶ ସେଟ୍ ସ୍ଥାପତ୍ୟ ( ISA ) ହେଉଛି ଏକ କମ୍ପ୍ୟୁଟରର ଏକ ଅବକ୍ଷୟ ମଡେଲ୍ | ଏହାକୁ ସ୍ଥାପତ୍ୟ କିମ୍ବା କମ୍ପ୍ୟୁଟର ସ୍ଥାପତ୍ୟ ମଧ୍ୟ କୁହାଯାଏ | ଏକ କେନ୍ଦ୍ରୀୟ ପ୍ରକ୍ରିୟାକରଣ ୟୁନିଟ୍ (CPU) ପରି ଏକ ISA ର ବାସ୍ତବତାକୁ ଏକ କାର୍ଯ୍ୟକାରିତା କୁହାଯାଏ |
ଗାଣିତିକ ତର୍କ ଏକକ: ଗଣନାରେ, ଏକ ଆରିଥମେଟିକ୍ ଲଜିକ୍ ୟୁନିଟ୍ (ALU) ହେଉଛି ଏକ ମିଳିତ ଡିଜିଟାଲ୍ ସର୍କିଟ୍ ଯାହା ଇଣ୍ଟିଜର୍ ବାଇନାରୀ ନମ୍ବର ଉପରେ ଗାଣିତିକ ଏବଂ ବିଟୱାଇସ୍ ଅପରେସନ୍ କରିଥାଏ | ଏହା ଏକ ଫ୍ଲୋଟିଂ ପଏଣ୍ଟ ୟୁନିଟ୍ (FPU) ର ବିପରୀତ, ଯାହା ଫ୍ଲୋଟିଂ ପଏଣ୍ଟ ନମ୍ବର ଉପରେ କାର୍ଯ୍ୟ କରେ | ଏହା କମ୍ପ୍ୟୁଟର, FPU ଏବଂ ଗ୍ରାଫିକ୍ସ ପ୍ରକ୍ରିୟାକରଣ ୟୁନିଟ୍ (ଜିପିୟୁ) ର କେନ୍ଦ୍ରୀୟ ପ୍ରକ୍ରିୟାକରଣ ୟୁନିଟ୍ (CPU) ଅନ୍ତର୍ଭୂକ୍ତ କରି ଅନେକ ପ୍ରକାରର ଗଣନା ସର୍କିଟ୍ ର ଏକ ମ fundamental ଳିକ ବିଲ୍ଡିଂ ବ୍ଲକ୍ |
ଗାଣିତିକ ତର୍କ ଏକକ: ଗଣନାରେ, ଏକ ଆରିଥମେଟିକ୍ ଲଜିକ୍ ୟୁନିଟ୍ (ALU) ହେଉଛି ଏକ ମିଳିତ ଡିଜିଟାଲ୍ ସର୍କିଟ୍ ଯାହା ଇଣ୍ଟିଜର୍ ବାଇନାରୀ ନମ୍ବର ଉପରେ ଗାଣିତିକ ଏବଂ ବିଟୱାଇସ୍ ଅପରେସନ୍ କରିଥାଏ | ଏହା ଏକ ଫ୍ଲୋଟିଂ ପଏଣ୍ଟ ୟୁନିଟ୍ (FPU) ର ବିପରୀତ, ଯାହା ଫ୍ଲୋଟିଂ ପଏଣ୍ଟ ନମ୍ବର ଉପରେ କାର୍ଯ୍ୟ କରେ | ଏହା କମ୍ପ୍ୟୁଟର, FPU ଏବଂ ଗ୍ରାଫିକ୍ସ ପ୍ରକ୍ରିୟାକରଣ ୟୁନିଟ୍ (ଜିପିୟୁ) ର କେନ୍ଦ୍ରୀୟ ପ୍ରକ୍ରିୟାକରଣ ୟୁନିଟ୍ (CPU) ଅନ୍ତର୍ଭୂକ୍ତ କରି ଅନେକ ପ୍ରକାରର ଗଣନା ସର୍କିଟ୍ ର ଏକ ମ fundamental ଳିକ ବିଲ୍ଡିଂ ବ୍ଲକ୍ |
ଗାଣିତିକ ତର୍କ ଏକକ: ଗଣନାରେ, ଏକ ଆରିଥମେଟିକ୍ ଲଜିକ୍ ୟୁନିଟ୍ (ALU) ହେଉଛି ଏକ ମିଳିତ ଡିଜିଟାଲ୍ ସର୍କିଟ୍ ଯାହା ଇଣ୍ଟିଜର୍ ବାଇନାରୀ ନମ୍ବର ଉପରେ ଗାଣିତିକ ଏବଂ ବିଟୱାଇସ୍ ଅପରେସନ୍ କରିଥାଏ | ଏହା ଏକ ଫ୍ଲୋଟିଂ ପଏଣ୍ଟ ୟୁନିଟ୍ (FPU) ର ବିପରୀତ, ଯାହା ଫ୍ଲୋଟିଂ ପଏଣ୍ଟ ନମ୍ବର ଉପରେ କାର୍ଯ୍ୟ କରେ | ଏହା କମ୍ପ୍ୟୁଟର, FPU ଏବଂ ଗ୍ରାଫିକ୍ସ ପ୍ରକ୍ରିୟାକରଣ ୟୁନିଟ୍ (ଜିପିୟୁ) ର କେନ୍ଦ୍ରୀୟ ପ୍ରକ୍ରିୟାକରଣ ୟୁନିଟ୍ (CPU) ଅନ୍ତର୍ଭୂକ୍ତ କରି ଅନେକ ପ୍ରକାରର ଗଣନା ସର୍କିଟ୍ ର ଏକ ମ fundamental ଳିକ ବିଲ୍ଡିଂ ବ୍ଲକ୍ |
ହାରାହାରି: କଥାବାର୍ତ୍ତା ଭାଷାରେ, ହାରାହାରି ହେଉଛି ଏକ ସଂଖ୍ୟା ଯାହାକି ଖାଲି ନଥିବା ତାଲିକାର ପ୍ରତିନିଧୀ ଭାବରେ ନିଆଯାଇଛି | ହାରାହାରି ବିଭିନ୍ନ ଧାରଣା ବିଭିନ୍ନ ପ୍ରସଙ୍ଗରେ ବ୍ୟବହୃତ ହୁଏ | ପ୍ରାୟତ "" ହାରାହାରି "ଗାଣିତିକ ଅର୍ଥକୁ ବୁ refers ାଏ, କେତେ ସଂଖ୍ୟା ହାରାହାରି ହୋଇ ବିଭକ୍ତ ସଂଖ୍ୟାଗୁଡ଼ିକର ସମଷ୍ଟି | ପରିସଂଖ୍ୟାନରେ, ଅର୍ଥ, ମଧ୍ୟମ, ଏବଂ ମୋଡ୍ ସମସ୍ତେ କେନ୍ଦ୍ରୀୟ ପ୍ରବୃତ୍ତିର ପଦକ୍ଷେପ ଭାବରେ ଜଣାଶୁଣା, ଏବଂ କଥାବାର୍ତ୍ତା ବ୍ୟବହାରରେ ଏଥି ମଧ୍ୟରୁ ଯେକ any ଣସିଟି ହାରାହାରି ମୂଲ୍ୟ କୁହାଯାଇପାରେ |
ଗାଣିତିକ ବିଲିୟର୍ଡ: ଚିତ୍ତାକର୍ଷକ ଗଣିତରେ, ଗାଣିତିକ ବିଲିୟର୍ଡଗୁଡିକ ଏକ ଆୟତକ୍ଷେତ୍ର ଭିତରେ ପ୍ରତିଫଳନ ବ୍ୟବହାର କରି ଦୁଇଟି ସାଧାରଣ ସଂଖ୍ୟାର ସର୍ବନିମ୍ନ ସାଧାରଣ ଏକାଧିକ ଏବଂ ସର୍ବ ବୃହତ ସାଧାରଣ ବିଭାଜକ ନିର୍ଣ୍ଣୟ କରିବା ପାଇଁ ଏକ ଜ୍ୟାମିତିକ ପଦ୍ଧତି ପ୍ରଦାନ କରନ୍ତି ଯାହାର ପାର୍ଶ୍ୱ ଦୁଇଟି ପ୍ରଦତ୍ତ ସଂଖ୍ୟା | ଗତିଶୀଳ ବିଲିୟର୍ଡଗୁଡିକର ଟ୍ରାଜେକ୍ଟୋରୀ ବିଶ୍ଳେଷଣର ଏହା ଏକ ସହଜ ଉଦାହରଣ |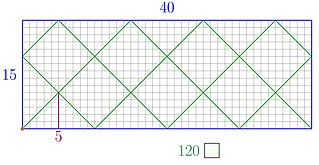
ଗାଣିତିକ ସର୍କିଟ ଜଟିଳତା: କମ୍ପ୍ୟୁଟେସନ୍ ଜଟିଳତା ସିଦ୍ଧାନ୍ତରେ, ଗାଣିତିକ ସର୍କିଟ୍ ହେଉଛି ପଲିନୋମିଆଲ୍ ଗଣନା ପାଇଁ ମାନକ ମଡେଲ୍ | ଅନ form ପଚାରିକ ଭାବରେ, ଏକ ଗାଣିତିକ ସର୍କିଟ୍ ଭେରିଏବଲ୍ କିମ୍ବା ସଂଖ୍ୟାକୁ ଇନପୁଟ୍ ଭାବରେ ଗ୍ରହଣ କରେ, ଏବଂ ଏହା ପୂର୍ବରୁ ଗଣିତ ଦୁଇଟି ଅଭିବ୍ୟକ୍ତି ଯୋଡିବା କିମ୍ବା ବ multip ାଇବାକୁ ଅନୁମତି ଦିଆଯାଏ | ଗଣନା ପଲିନୋମିଆଲ୍ସର ଜଟିଳତାକୁ ବୁ to ିବା ପାଇଁ ଆରିଥମେଟିକ୍ ସର୍କିଟ୍ ଏକ ଆନୁଷ୍ଠାନିକ ଉପାୟ ପ୍ରଦାନ କରେ | ଅନୁସନ୍ଧାନର ଏହି ଧାଡିରେ ମ basic ଳିକ ପ୍ରକାରର ପ୍ରଶ୍ନ ହେଉଛି "ପ୍ରଦତ୍ତ ବହୁଭୂତ ଗଣନା କରିବାର ସବୁଠାରୁ ଦକ୍ଷ ଉପାୟ କ'ଣ? ? "
ଗାଣିତିକ ସର୍କିଟ ଜଟିଳତା: କମ୍ପ୍ୟୁଟେସନ୍ ଜଟିଳତା ସିଦ୍ଧାନ୍ତରେ, ଗାଣିତିକ ସର୍କିଟ୍ ହେଉଛି ପଲିନୋମିଆଲ୍ ଗଣନା ପାଇଁ ମାନକ ମଡେଲ୍ | ଅନ form ପଚାରିକ ଭାବରେ, ଏକ ଗାଣିତିକ ସର୍କିଟ୍ ଭେରିଏବଲ୍ କିମ୍ବା ସଂଖ୍ୟାକୁ ଇନପୁଟ୍ ଭାବରେ ଗ୍ରହଣ କରେ, ଏବଂ ଏହା ପୂର୍ବରୁ ଗଣିତ ଦୁଇଟି ଅଭିବ୍ୟକ୍ତି ଯୋଡିବା କିମ୍ବା ବ multip ାଇବାକୁ ଅନୁମତି ଦିଆଯାଏ | ଗଣନା ପଲିନୋମିଆଲ୍ସର ଜଟିଳତାକୁ ବୁ to ିବା ପାଇଁ ଆରିଥମେଟିକ୍ ସର୍କିଟ୍ ଏକ ଆନୁଷ୍ଠାନିକ ଉପାୟ ପ୍ରଦାନ କରେ | ଅନୁସନ୍ଧାନର ଏହି ଧାଡିରେ ମ basic ଳିକ ପ୍ରକାରର ପ୍ରଶ୍ନ ହେଉଛି "ପ୍ରଦତ୍ତ ବହୁଭୂତ ଗଣନା କରିବାର ସବୁଠାରୁ ଦକ୍ଷ ଉପାୟ କ'ଣ? ? "
ଗାଣିତିକ ସର୍କିଟ ଜଟିଳତା: କମ୍ପ୍ୟୁଟେସନ୍ ଜଟିଳତା ସିଦ୍ଧାନ୍ତରେ, ଗାଣିତିକ ସର୍କିଟ୍ ହେଉଛି ପଲିନୋମିଆଲ୍ ଗଣନା ପାଇଁ ମାନକ ମଡେଲ୍ | ଅନ form ପଚାରିକ ଭାବରେ, ଏକ ଗାଣିତିକ ସର୍କିଟ୍ ଭେରିଏବଲ୍ କିମ୍ବା ସଂଖ୍ୟାକୁ ଇନପୁଟ୍ ଭାବରେ ଗ୍ରହଣ କରେ, ଏବଂ ଏହା ପୂର୍ବରୁ ଗଣିତ ଦୁଇଟି ଅଭିବ୍ୟକ୍ତି ଯୋଡିବା କିମ୍ବା ବ multip ାଇବାକୁ ଅନୁମତି ଦିଆଯାଏ | ଗଣନା ପଲିନୋମିଆଲ୍ସର ଜଟିଳତାକୁ ବୁ to ିବା ପାଇଁ ଆରିଥମେଟିକ୍ ସର୍କିଟ୍ ଏକ ଆନୁଷ୍ଠାନିକ ଉପାୟ ପ୍ରଦାନ କରେ | ଅନୁସନ୍ଧାନର ଏହି ଧାଡିରେ ମ basic ଳିକ ପ୍ରକାରର ପ୍ରଶ୍ନ ହେଉଛି "ପ୍ରଦତ୍ତ ବହୁଭୂତ ଗଣନା କରିବାର ସବୁଠାରୁ ଦକ୍ଷ ଉପାୟ କ'ଣ? ? "
ଗାଣିତିକ ସର୍କିଟ ଜଟିଳତା: କମ୍ପ୍ୟୁଟେସନ୍ ଜଟିଳତା ସିଦ୍ଧାନ୍ତରେ, ଗାଣିତିକ ସର୍କିଟ୍ ହେଉଛି ପଲିନୋମିଆଲ୍ ଗଣନା ପାଇଁ ମାନକ ମଡେଲ୍ | ଅନ form ପଚାରିକ ଭାବରେ, ଏକ ଗାଣିତିକ ସର୍କିଟ୍ ଭେରିଏବଲ୍ କିମ୍ବା ସଂଖ୍ୟାକୁ ଇନପୁଟ୍ ଭାବରେ ଗ୍ରହଣ କରେ, ଏବଂ ଏହା ପୂର୍ବରୁ ଗଣିତ ଦୁଇଟି ଅଭିବ୍ୟକ୍ତି ଯୋଡିବା କିମ୍ବା ବ multip ାଇବାକୁ ଅନୁମତି ଦିଆଯାଏ | ଗଣନା ପଲିନୋମିଆଲ୍ସର ଜଟିଳତାକୁ ବୁ to ିବା ପାଇଁ ଆରିଥମେଟିକ୍ ସର୍କିଟ୍ ଏକ ଆନୁଷ୍ଠାନିକ ଉପାୟ ପ୍ରଦାନ କରେ | ଅନୁସନ୍ଧାନର ଏହି ଧାଡିରେ ମ basic ଳିକ ପ୍ରକାରର ପ୍ରଶ୍ନ ହେଉଛି "ପ୍ରଦତ୍ତ ବହୁଭୂତ ଗଣନା କରିବାର ସବୁଠାରୁ ଦକ୍ଷ ଉପାୟ କ'ଣ? ? "
ଗାଣିତିକ କୋଡିଂ: ଆରିଥମେଟିକ୍ କୋଡିଂ ହେଉଛି କ୍ଷତିହୀନ ଡାଟା ସଙ୍କୋଚନରେ ବ୍ୟବହୃତ ଏଣ୍ଟ୍ରପି ଏନକୋଡିଂର ଏକ ରୂପ | ସାଧାରଣତ ,, ASCII କୋଡ୍ ପରି ଅକ୍ଷରଗୁଡିକର ଏକ ଷ୍ଟ୍ରିଙ୍ଗ୍ ଯେପରିକି "ହେଲୋ ସେଠାରେ" ଶବ୍ଦଗୁଡିକ ପ୍ରତି ଅକ୍ଷର ପ୍ରତି ନିର୍ଦ୍ଦିଷ୍ଟ ସଂଖ୍ୟକ ବିଟ୍ ବ୍ୟବହାର କରି ଉପସ୍ଥାପିତ ହୁଏ | ଯେତେବେଳେ ଏକ ଷ୍ଟ୍ରିଙ୍ଗ୍ ଆରିଥମେଟିକ୍ ଏନକୋଡିଂରେ ରୂପାନ୍ତରିତ ହୁଏ, ବାରମ୍ବାର ବ୍ୟବହୃତ ଅକ୍ଷରଗୁଡ଼ିକ କମ୍ ବିଟ୍ ସହିତ ଗଚ୍ଛିତ ହେବ ଏବଂ ବାରମ୍ବାର ଘଟୁଥିବା ଅକ୍ଷରଗୁଡିକ ଅଧିକ ବିଟ୍ ସହିତ ଗଚ୍ଛିତ ହେବ, ଫଳସ୍ୱରୂପ ସମୁଦାୟ ବ୍ୟବହୃତ କମ୍ ବିଟ୍ | ଆରିଥମେଟିକ୍ କୋଡିଂ ଅନ୍ୟ ପ୍ରକାର ଏଣ୍ଟ୍ରପି ଏନକୋଡିଂ ଠାରୁ ଭିନ୍ନ, ଯେପରିକି ହଫମାନ କୋଡିଂ, ଏଥିରେ ଇନପୁଟକୁ ଉପାଦାନ ସଙ୍କେତରେ ପୃଥକ କରିବା ଏବଂ ପ୍ରତ୍ୟେକକୁ ଏକ କୋଡ୍ ସହିତ ବଦଳାଇବା ପରିବର୍ତ୍ତେ, ଆରିଥମେଟିକ୍ କୋଡିଂ ସମଗ୍ର ସନ୍ଦେଶକୁ ଏକ ନମ୍ବରରେ ଏନକୋଡ୍ କରେ, ଏକ ଇଚ୍ଛାଧୀନ-ସଠିକତା ଭଗ୍ନାଂଶ q ଯେଉଁଠାରେ 0.0 ≤ q <1.0। ଏହା ସାମ୍ପ୍ରତିକ ସୂଚନାକୁ ଏକ ପରିସର ଭାବରେ ଦର୍ଶାଏ, ଦୁଇଟି ସଂଖ୍ୟା ଦ୍ୱାରା ବ୍ୟାଖ୍ୟା କରାଯାଇଛି | ଅସୀମେଟ୍ରିକ୍ ସାଂଖ୍ୟିକ ପ୍ରଣାଳୀ ନାମକ ଏକ ଏଣ୍ଟ୍ରପି କୋଡର୍ ର ଏକ ପରିବାର ବର୍ତ୍ତମାନର ସୂଚନାକୁ ପ୍ରତିନିଧିତ୍ୱ କରୁଥିବା ଏକ ପ୍ରାକୃତିକ ସଂଖ୍ୟାରେ ସିଧାସଳଖ କାର୍ଯ୍ୟ କରିଥିବାରୁ ଶୀଘ୍ର କାର୍ଯ୍ୟକାରିତା ପାଇଁ ଅନୁମତି ଦେଇଥାଏ |
ଗାଣିତିକ କୋଡିଂ: ଆରିଥମେଟିକ୍ କୋଡିଂ ହେଉଛି କ୍ଷତିହୀନ ଡାଟା ସଙ୍କୋଚନରେ ବ୍ୟବହୃତ ଏଣ୍ଟ୍ରପି ଏନକୋଡିଂର ଏକ ରୂପ | ସାଧାରଣତ ,, ASCII କୋଡ୍ ପରି ଅକ୍ଷରଗୁଡିକର ଏକ ଷ୍ଟ୍ରିଙ୍ଗ୍ ଯେପରିକି "ହେଲୋ ସେଠାରେ" ଶବ୍ଦଗୁଡିକ ପ୍ରତି ଅକ୍ଷର ପ୍ରତି ନିର୍ଦ୍ଦିଷ୍ଟ ସଂଖ୍ୟକ ବିଟ୍ ବ୍ୟବହାର କରି ଉପସ୍ଥାପିତ ହୁଏ | ଯେତେବେଳେ ଏକ ଷ୍ଟ୍ରିଙ୍ଗ୍ ଆରିଥମେଟିକ୍ ଏନକୋଡିଂରେ ରୂପାନ୍ତରିତ ହୁଏ, ବାରମ୍ବାର ବ୍ୟବହୃତ ଅକ୍ଷରଗୁଡ଼ିକ କମ୍ ବିଟ୍ ସହିତ ଗଚ୍ଛିତ ହେବ ଏବଂ ବାରମ୍ବାର ଘଟୁଥିବା ଅକ୍ଷରଗୁଡିକ ଅଧିକ ବିଟ୍ ସହିତ ଗଚ୍ଛିତ ହେବ, ଫଳସ୍ୱରୂପ ସମୁଦାୟ ବ୍ୟବହୃତ କମ୍ ବିଟ୍ | ଆରିଥମେଟିକ୍ କୋଡିଂ ଅନ୍ୟ ପ୍ରକାର ଏଣ୍ଟ୍ରପି ଏନକୋଡିଂ ଠାରୁ ଭିନ୍ନ, ଯେପରିକି ହଫମାନ କୋଡିଂ, ଏଥିରେ ଇନପୁଟକୁ ଉପାଦାନ ସଙ୍କେତରେ ପୃଥକ କରିବା ଏବଂ ପ୍ରତ୍ୟେକକୁ ଏକ କୋଡ୍ ସହିତ ବଦଳାଇବା ପରିବର୍ତ୍ତେ, ଆରିଥମେଟିକ୍ କୋଡିଂ ସମଗ୍ର ସନ୍ଦେଶକୁ ଏକ ନମ୍ବରରେ ଏନକୋଡ୍ କରେ, ଏକ ଇଚ୍ଛାଧୀନ-ସଠିକତା ଭଗ୍ନାଂଶ q ଯେଉଁଠାରେ 0.0 ≤ q <1.0। ଏହା ସାମ୍ପ୍ରତିକ ସୂଚନାକୁ ଏକ ପରିସର ଭାବରେ ଦର୍ଶାଏ, ଦୁଇଟି ସଂଖ୍ୟା ଦ୍ୱାରା ବ୍ୟାଖ୍ୟା କରାଯାଇଛି | ଅସୀମେଟ୍ରିକ୍ ସାଂଖ୍ୟିକ ପ୍ରଣାଳୀ ନାମକ ଏକ ଏଣ୍ଟ୍ରପି କୋଡର୍ ର ଏକ ପରିବାର ବର୍ତ୍ତମାନର ସୂଚନାକୁ ପ୍ରତିନିଧିତ୍ୱ କରୁଥିବା ଏକ ପ୍ରାକୃତିକ ସଂଖ୍ୟାରେ ସିଧାସଳଖ କାର୍ଯ୍ୟ କରିଥିବାରୁ ଶୀଘ୍ର କାର୍ଯ୍ୟକାରିତା ପାଇଁ ଅନୁମତି ଦେଇଥାଏ |
ଗାଣିତିକ କୋଡିଂ: ଆରିଥମେଟିକ୍ କୋଡିଂ ହେଉଛି କ୍ଷତିହୀନ ଡାଟା ସଙ୍କୋଚନରେ ବ୍ୟବହୃତ ଏଣ୍ଟ୍ରପି ଏନକୋଡିଂର ଏକ ରୂପ | ସାଧାରଣତ ,, ASCII କୋଡ୍ ପରି ଅକ୍ଷରଗୁଡିକର ଏକ ଷ୍ଟ୍ରିଙ୍ଗ୍ ଯେପରିକି "ହେଲୋ ସେଠାରେ" ଶବ୍ଦଗୁଡିକ ପ୍ରତି ଅକ୍ଷର ପ୍ରତି ନିର୍ଦ୍ଦିଷ୍ଟ ସଂଖ୍ୟକ ବିଟ୍ ବ୍ୟବହାର କରି ଉପସ୍ଥାପିତ ହୁଏ | ଯେତେବେଳେ ଏକ ଷ୍ଟ୍ରିଙ୍ଗ୍ ଆରିଥମେଟିକ୍ ଏନକୋଡିଂରେ ରୂପାନ୍ତରିତ ହୁଏ, ବାରମ୍ବାର ବ୍ୟବହୃତ ଅକ୍ଷରଗୁଡ଼ିକ କମ୍ ବିଟ୍ ସହିତ ଗଚ୍ଛିତ ହେବ ଏବଂ ବାରମ୍ବାର ଘଟୁଥିବା ଅକ୍ଷରଗୁଡିକ ଅଧିକ ବିଟ୍ ସହିତ ଗଚ୍ଛିତ ହେବ, ଫଳସ୍ୱରୂପ ସମୁଦାୟ ବ୍ୟବହୃତ କମ୍ ବିଟ୍ | ଆରିଥମେଟିକ୍ କୋଡିଂ ଅନ୍ୟ ପ୍ରକାର ଏଣ୍ଟ୍ରପି ଏନକୋଡିଂ ଠାରୁ ଭିନ୍ନ, ଯେପରିକି ହଫମାନ କୋଡିଂ, ଏଥିରେ ଇନପୁଟକୁ ଉପାଦାନ ସଙ୍କେତରେ ପୃଥକ କରିବା ଏବଂ ପ୍ରତ୍ୟେକକୁ ଏକ କୋଡ୍ ସହିତ ବଦଳାଇବା ପରିବର୍ତ୍ତେ, ଆରିଥମେଟିକ୍ କୋଡିଂ ସମଗ୍ର ସନ୍ଦେଶକୁ ଏକ ନମ୍ବରରେ ଏନକୋଡ୍ କରେ, ଏକ ଇଚ୍ଛାଧୀନ-ସଠିକତା ଭଗ୍ନାଂଶ q ଯେଉଁଠାରେ 0.0 ≤ q <1.0। ଏହା ସାମ୍ପ୍ରତିକ ସୂଚନାକୁ ଏକ ପରିସର ଭାବରେ ଦର୍ଶାଏ, ଦୁଇଟି ସଂଖ୍ୟା ଦ୍ୱାରା ବ୍ୟାଖ୍ୟା କରାଯାଇଛି | ଅସୀମେଟ୍ରିକ୍ ସାଂଖ୍ୟିକ ପ୍ରଣାଳୀ ନାମକ ଏକ ଏଣ୍ଟ୍ରପି କୋଡର୍ ର ଏକ ପରିବାର ବର୍ତ୍ତମାନର ସୂଚନାକୁ ପ୍ରତିନିଧିତ୍ୱ କରୁଥିବା ଏକ ପ୍ରାକୃତିକ ସଂଖ୍ୟାରେ ସିଧାସଳଖ କାର୍ଯ୍ୟ କରିଥିବାରୁ ଶୀଘ୍ର କାର୍ଯ୍ୟକାରିତା ପାଇଁ ଅନୁମତି ଦେଇଥାଏ |
ଗାଣିତିକ ସଂଯୋଜକ: ଗଣିତରେ, ଗଣିତ କମ୍ବିନେଟେରିକ୍ସ ହେଉଛି ସଂଖ୍ୟା ଥିଓରୀ, କମ୍ବିନେଟେରିକ୍ସ, ଏର୍ଗୋଡିକ୍ ସିଦ୍ଧାନ୍ତ ଏବଂ ହାରମୋନିକ୍ ବିଶ୍ଳେଷଣର ଛକ |
ଫାଷ୍ଟ ଫୋରିଅର୍ ଟ୍ରାନ୍ସଫର୍ମ: ଏକ ଦ୍ରୁତ ଫୁରିଅର୍ ଟ୍ରାନ୍ସଫର୍ମ ( FFT ) ହେଉଛି ଏକ ଆଲଗୋରିଦମ ଯାହା ଏକ କ୍ରମର ବିଚ୍ଛିନ୍ନ ଫୋରିଅର୍ ଟ୍ରାନ୍ସଫର୍ମ (DFT) କିମ୍ବା ଏହାର ଓଲଟା (IDFT) ଗଣନା କରେ | ଫୋରିଅର୍ ଆନାଲିସିସ୍ ଏହାର ମୂଳ ଡୋମେନ୍ ରୁ ଏକ ସଙ୍କେତକୁ ଫ୍ରିକ୍ୱେନ୍ସି ଡୋମେନ୍ ରେ ଏକ ପ୍ରତିନିଧିତ୍ୱରେ ପରିଣତ କରେ | ବିଭିନ୍ନ ଫ୍ରିକ୍ୱେନ୍ସିର ଉପାଦାନଗୁଡ଼ିକରେ ମୂଲ୍ୟଗୁଡ଼ିକର କ୍ରମକୁ ଖଣ୍ଡ କରି DFT ପ୍ରାପ୍ତ ହୁଏ | ଏହି ଅପରେସନ୍ ଅନେକ କ୍ଷେତ୍ରରେ ଉପଯୋଗୀ, କିନ୍ତୁ ଏହାକୁ ସଂଜ୍ଞା ଠାରୁ ସିଧାସଳଖ ଗଣନା କରିବା ପ୍ରାୟତ practical ବ୍ୟବହାରିକ ହେବା ପାଇଁ ବହୁତ ଧୀର ଅଟେ | ଏକ FFT ଦ୍ରୁତ ଗତିରେ DFT ମ୍ୟାଟ୍ରିକ୍ସକୁ ଅଳ୍ପ କାରକଗୁଡିକର ଉତ୍ପାଦରେ ଫ୍ୟାକ୍ଟ୍ରି କରି ଏହିପରି ପରିବର୍ତ୍ତନଗୁଡ଼ିକୁ ଗଣନା କରେ | ଫଳସ୍ୱରୂପ, ଏହା DFT ଗଣନା କରିବାର ଜଟିଳତାକୁ ହ୍ରାସ କରିବାକୁ ପରିଚାଳନା କରେ | , ଯାହା ଉତ୍ପନ୍ନ ହୁଏ ଯଦି ଜଣେ କେବଳ DFT ର ସଂଜ୍ଞା ପ୍ରୟୋଗ କରେ, , କେଉଁଠାରେ ହେଉଛି ଡାଟା ସାଇଜ୍ | ଗତିର ପାର୍ଥକ୍ୟ ବହୁତ ବଡ ହୋଇପାରେ, ବିଶେଷତ long ଲମ୍ବା ଡାଟା ସେଟ୍ ପାଇଁ ଯେଉଁଠାରେ N ହଜାର କିମ୍ବା ଲକ୍ଷରେ ଥାଇପାରେ | ରାଉଣ୍ଡ-ଅଫ୍ ତ୍ରୁଟିର ଉପସ୍ଥିତିରେ, ଅନେକ FFT ଆଲଗୋରିଦମ DFT ସଂଜ୍ଞାକୁ ପ୍ରତ୍ୟକ୍ଷ କିମ୍ବା ପରୋକ୍ଷ ଭାବରେ ମୂଲ୍ୟାଙ୍କନ କରିବା ଅପେକ୍ଷା ଅଧିକ ସଠିକ୍ | ସରଳ ଜଟିଳ-ସଂଖ୍ୟା ଗଣିତ ଠାରୁ ଆରମ୍ଭ କରି ଗୋଷ୍ଠୀ ତତ୍ତ୍ and ଏବଂ ସଂଖ୍ୟା ଥିଓରୀ ପର୍ଯ୍ୟନ୍ତ ବିଭିନ୍ନ ପ୍ରକାଶିତ ଥିଓରୀ ଉପରେ ଆଧାର କରି ଅନେକ ଭିନ୍ନ FFT ଆଲଗୋରିଦମ ଅଛି |
ଫାଷ୍ଟ ଫୋରିଅର୍ ଟ୍ରାନ୍ସଫର୍ମ: ଏକ ଦ୍ରୁତ ଫୁରିଅର୍ ଟ୍ରାନ୍ସଫର୍ମ ( FFT ) ହେଉଛି ଏକ ଆଲଗୋରିଦମ ଯାହା ଏକ କ୍ରମର ବିଚ୍ଛିନ୍ନ ଫୋରିଅର୍ ଟ୍ରାନ୍ସଫର୍ମ (DFT) କିମ୍ବା ଏହାର ଓଲଟା (IDFT) ଗଣନା କରେ | ଫୋରିଅର୍ ଆନାଲିସିସ୍ ଏହାର ମୂଳ ଡୋମେନ୍ ରୁ ଏକ ସଙ୍କେତକୁ ଫ୍ରିକ୍ୱେନ୍ସି ଡୋମେନ୍ ରେ ଏକ ପ୍ରତିନିଧିତ୍ୱରେ ପରିଣତ କରେ | ବିଭିନ୍ନ ଫ୍ରିକ୍ୱେନ୍ସିର ଉପାଦାନଗୁଡ଼ିକରେ ମୂଲ୍ୟଗୁଡ଼ିକର କ୍ରମକୁ ଖଣ୍ଡ କରି DFT ପ୍ରାପ୍ତ ହୁଏ | ଏହି ଅପରେସନ୍ ଅନେକ କ୍ଷେତ୍ରରେ ଉପଯୋଗୀ, କିନ୍ତୁ ଏହାକୁ ସଂଜ୍ଞା ଠାରୁ ସିଧାସଳଖ ଗଣନା କରିବା ପ୍ରାୟତ practical ବ୍ୟବହାରିକ ହେବା ପାଇଁ ବହୁତ ଧୀର ଅଟେ | ଏକ FFT ଦ୍ରୁତ ଗତିରେ DFT ମ୍ୟାଟ୍ରିକ୍ସକୁ ଅଳ୍ପ କାରକଗୁଡିକର ଉତ୍ପାଦରେ ଫ୍ୟାକ୍ଟ୍ରି କରି ଏହିପରି ପରିବର୍ତ୍ତନଗୁଡ଼ିକୁ ଗଣନା କରେ | ଫଳସ୍ୱରୂପ, ଏହା DFT ଗଣନା କରିବାର ଜଟିଳତାକୁ ହ୍ରାସ କରିବାକୁ ପରିଚାଳନା କରେ | , ଯାହା ଉତ୍ପନ୍ନ ହୁଏ ଯଦି ଜଣେ କେବଳ DFT ର ସଂଜ୍ଞା ପ୍ରୟୋଗ କରେ, , କେଉଁଠାରେ ହେଉଛି ଡାଟା ସାଇଜ୍ | ଗତିର ପାର୍ଥକ୍ୟ ବହୁତ ବଡ ହୋଇପାରେ, ବିଶେଷତ long ଲମ୍ବା ଡାଟା ସେଟ୍ ପାଇଁ ଯେଉଁଠାରେ N ହଜାର କିମ୍ବା ଲକ୍ଷରେ ଥାଇପାରେ | ରାଉଣ୍ଡ-ଅଫ୍ ତ୍ରୁଟିର ଉପସ୍ଥିତିରେ, ଅନେକ FFT ଆଲଗୋରିଦମ DFT ସଂଜ୍ଞାକୁ ପ୍ରତ୍ୟକ୍ଷ କିମ୍ବା ପରୋକ୍ଷ ଭାବରେ ମୂଲ୍ୟାଙ୍କନ କରିବା ଅପେକ୍ଷା ଅଧିକ ସଠିକ୍ | ସରଳ ଜଟିଳ-ସଂଖ୍ୟା ଗଣିତ ଠାରୁ ଆରମ୍ଭ କରି ଗୋଷ୍ଠୀ ତତ୍ତ୍ and ଏବଂ ସଂଖ୍ୟା ଥିଓରୀ ପର୍ଯ୍ୟନ୍ତ ବିଭିନ୍ନ ପ୍ରକାଶିତ ଥିଓରୀ ଉପରେ ଆଧାର କରି ଅନେକ ଭିନ୍ନ FFT ଆଲଗୋରିଦମ ଅଛି |
ଆନ୍ତ universal- ସର୍ବଭାରତୀୟ ଟେକ୍ମୁଲର୍ ସିଦ୍ଧାନ୍ତ: ଆନ୍ତ universal- ସର୍ବଭାରତୀୟ ଟେଚମୁଲର୍ ସିଦ୍ଧାନ୍ତ ହେଉଛି ଗଣିତଜ୍ଞ ସିନିଚି ମୋଚିଜୁକିଙ୍କ ଦ୍ 2000 ାରା 2000 ଦଶକରେ ବିକଶିତ ହୋଇଥିବା ଏକ ତତ୍ତ୍ to କୁ ସେ ଆରିଥମେଟିକ୍ ଜ୍ୟାମିତିର ପୂର୍ବ କାର୍ଯ୍ୟ ଅନୁସରଣ କରିଥିଲେ | ମୋଚିଜୁକିଙ୍କ ଅନୁଯାୟୀ, ଏହା ହେଉଛି ଏକ ଏଲିପଟିକ୍ ବକ୍ର ସହିତ ସଜ୍ଜିତ ସଂଖ୍ୟା କ୍ଷେତ୍ର ପାଇଁ ଟେଚମୁଲର୍ ସିଦ୍ଧାନ୍ତର ଏକ ଆରିଥମେଟିକ୍ ସଂସ୍କରଣ | 2012 ରେ ତାଙ୍କ ୱେବସାଇଟରେ ପୋଷ୍ଟ ହୋଇଥିବା ଚାରୋଟି ପ୍ରିଣ୍ଟ୍ର କ୍ରମରେ ଏହି ସିଦ୍ଧାନ୍ତ ସାର୍ବଜନୀନ କରାଯାଇଥିଲା | ସିଦ୍ଧାନ୍ତର ସବୁଠାରୁ ଚମତ୍କାର ଦାବି ହେଉଛି ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତରେ ବିଭିନ୍ନ ଉଲ୍ଲେଖନୀୟ ଧାରଣା ପାଇଁ ଏକ ପ୍ରମାଣ ପ୍ରଦାନ କରିବା, ବିଶେଷତ ab abc ଧାରଣା | ମୋଚିଜୁକି ଏବଂ ଅନ୍ୟ କେତେକ ଗଣିତଜ୍ claim ମାନେ ଦାବି କରନ୍ତି ଯେ ସିଦ୍ଧାନ୍ତ ପ୍ରକୃତରେ ଏପରି ପ୍ରମାଣ ଦେଇଥାଏ କିନ୍ତୁ ଏପର୍ଯ୍ୟନ୍ତ ଏହା ଗଣିତ ସମ୍ପ୍ରଦାୟ ଦ୍ୱାରା ଗ୍ରହଣ କରାଯାଇ ନାହିଁ |
ପ୍ରାକୃତିକ ଘନତା: ସଂଖ୍ୟା ତତ୍ତ୍ In ରେ, ପ୍ରାକୃତିକ ଘନତା ହେଉଛି ପ୍ରାକୃତିକ ସଂଖ୍ୟାଗୁଡ଼ିକର ସେଟ୍ ର ଏକ ସବ୍ସେଟ୍ କେତେ ବଡ଼ ତାହା ମାପିବା ପାଇଁ ଗୋଟିଏ ପଦ୍ଧତି | ଏହା ମୁଖ୍ୟତ the ଇଚ୍ଛିତ ଉପସେଟର ସଦସ୍ୟମାନଙ୍କ ସାମ୍ନା କରିବାର ସମ୍ଭାବନା ଉପରେ ନିର୍ଭର କରେ [ n , n ] ବ୍ୟବଧାନରେ କମ୍ବିଂ କରିବା ସମୟରେ n ବଡ ହୋଇଯାଏ |
ଗାଣିତିକ derivative: ସଂଖ୍ୟା ତତ୍ତ୍ In ରେ, ଲାଗାରିଆସ୍ ଆରିଥମେଟିକ୍ ଡେରିଭେଟିଭ୍ , କିମ୍ବା ସଂଖ୍ୟା ଡେରିଭେଟିଭ୍ , ଇଣ୍ଟିଜର୍ସ ପାଇଁ ବ୍ୟାଖ୍ୟା କରାଯାଇଥିବା ଏକ କାର୍ଯ୍ୟ, ପ୍ରାଇମ ଫ୍ୟାକ୍ଟ୍ରାଇଜେସନ୍ ଉପରେ ଆଧାର କରି, ଏକ କାର୍ଯ୍ୟର ଡେରିଭେଟିଭ୍ ପାଇଁ ଉତ୍ପାଦ ନିୟମ ସହିତ ଅନୁରୂପ ଯାହା ଗାଣିତିକ ବିଶ୍ଳେଷଣରେ ବ୍ୟବହୃତ ହୁଏ |
ଗାଣିତିକ ଗତିଶୀଳତା: ଗାଣିତିକ ଗତିଶୀଳତା ହେଉଛି ଏକ କ୍ଷେତ୍ର ଯାହା ଗଣିତର ଦୁଇଟି କ୍ଷେତ୍ର, ଗତିଶୀଳ ପ୍ରଣାଳୀ ଏବଂ ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତକୁ ଏକତ୍ର କରିଥାଏ | ଶାସ୍ତ୍ରୀୟ ଭାବରେ, ବିଚ୍ଛିନ୍ନ ଗତିଶୀଳତା ଜଟିଳ ବିମାନ କିମ୍ବା ପ୍ରକୃତ ଲାଇନର ସ୍ୱ-ମାନଚିତ୍ରର ପୁନରାବୃତ୍ତି ଅଧ୍ୟୟନକୁ ବୁ .ାଏ | ଆରିଥମେଟିକ୍ ଗତିଶୀଳତା ହେଉଛି ବହୁସଂଖ୍ୟକ କିମ୍ବା ଯୁକ୍ତିଯୁକ୍ତ କାର୍ଯ୍ୟର ବାରମ୍ବାର ପ୍ରୟୋଗରେ ଇଣ୍ଟିଜର୍, ଯୁକ୍ତିଯୁକ୍ତ, p- ପ୍ୟାଡିକ୍, ଏବଂ / କିମ୍ବା ବୀଜ ବର୍ଣ୍ଣିତ ପଏଣ୍ଟଗୁଡିକର ସଂଖ୍ୟା-ତତ୍ତ୍ୱିକ ଗୁଣଗୁଡିକର ଅଧ୍ୟୟନ | ଏକ ମ fundamental ଳିକ ଲକ୍ଷ୍ୟ ହେଉଛି ଅନ୍ତର୍ନିହିତ ଜ୍ୟାମିତିକ ସଂରଚନା ଦୃଷ୍ଟିରୁ ଗାଣିତିକ ଗୁଣ ବର୍ଣ୍ଣନା କରିବା |
ଗାଣିତିକ କୋଡିଂ: ଆରିଥମେଟିକ୍ କୋଡିଂ ହେଉଛି କ୍ଷତିହୀନ ଡାଟା ସଙ୍କୋଚନରେ ବ୍ୟବହୃତ ଏଣ୍ଟ୍ରପି ଏନକୋଡିଂର ଏକ ରୂପ | ସାଧାରଣତ ,, ASCII କୋଡ୍ ପରି ଅକ୍ଷରଗୁଡିକର ଏକ ଷ୍ଟ୍ରିଙ୍ଗ୍ ଯେପରିକି "ହେଲୋ ସେଠାରେ" ଶବ୍ଦଗୁଡିକ ପ୍ରତି ଅକ୍ଷର ପ୍ରତି ନିର୍ଦ୍ଦିଷ୍ଟ ସଂଖ୍ୟକ ବିଟ୍ ବ୍ୟବହାର କରି ଉପସ୍ଥାପିତ ହୁଏ | ଯେତେବେଳେ ଏକ ଷ୍ଟ୍ରିଙ୍ଗ୍ ଆରିଥମେଟିକ୍ ଏନକୋଡିଂରେ ରୂପାନ୍ତରିତ ହୁଏ, ବାରମ୍ବାର ବ୍ୟବହୃତ ଅକ୍ଷରଗୁଡ଼ିକ କମ୍ ବିଟ୍ ସହିତ ଗଚ୍ଛିତ ହେବ ଏବଂ ବାରମ୍ବାର ଘଟୁଥିବା ଅକ୍ଷରଗୁଡିକ ଅଧିକ ବିଟ୍ ସହିତ ଗଚ୍ଛିତ ହେବ, ଫଳସ୍ୱରୂପ ସମୁଦାୟ ବ୍ୟବହୃତ କମ୍ ବିଟ୍ | ଆରିଥମେଟିକ୍ କୋଡିଂ ଅନ୍ୟ ପ୍ରକାର ଏଣ୍ଟ୍ରପି ଏନକୋଡିଂ ଠାରୁ ଭିନ୍ନ, ଯେପରିକି ହଫମାନ କୋଡିଂ, ଏଥିରେ ଇନପୁଟକୁ ଉପାଦାନ ସଙ୍କେତରେ ପୃଥକ କରିବା ଏବଂ ପ୍ରତ୍ୟେକକୁ ଏକ କୋଡ୍ ସହିତ ବଦଳାଇବା ପରିବର୍ତ୍ତେ, ଆରିଥମେଟିକ୍ କୋଡିଂ ସମଗ୍ର ସନ୍ଦେଶକୁ ଏକ ନମ୍ବରରେ ଏନକୋଡ୍ କରେ, ଏକ ଇଚ୍ଛାଧୀନ-ସଠିକତା ଭଗ୍ନାଂଶ q ଯେଉଁଠାରେ 0.0 ≤ q <1.0। ଏହା ସାମ୍ପ୍ରତିକ ସୂଚନାକୁ ଏକ ପରିସର ଭାବରେ ଦର୍ଶାଏ, ଦୁଇଟି ସଂଖ୍ୟା ଦ୍ୱାରା ବ୍ୟାଖ୍ୟା କରାଯାଇଛି | ଅସୀମେଟ୍ରିକ୍ ସାଂଖ୍ୟିକ ପ୍ରଣାଳୀ ନାମକ ଏକ ଏଣ୍ଟ୍ରପି କୋଡର୍ ର ଏକ ପରିବାର ବର୍ତ୍ତମାନର ସୂଚନାକୁ ପ୍ରତିନିଧିତ୍ୱ କରୁଥିବା ଏକ ପ୍ରାକୃତିକ ସଂଖ୍ୟାରେ ସିଧାସଳଖ କାର୍ଯ୍ୟ କରିଥିବାରୁ ଶୀଘ୍ର କାର୍ଯ୍ୟକାରିତା ପାଇଁ ଅନୁମତି ଦେଇଥାଏ |
ଗାଣିତିକ କୋଡିଂ: ଆରିଥମେଟିକ୍ କୋଡିଂ ହେଉଛି କ୍ଷତିହୀନ ଡାଟା ସଙ୍କୋଚନରେ ବ୍ୟବହୃତ ଏଣ୍ଟ୍ରପି ଏନକୋଡିଂର ଏକ ରୂପ | ସାଧାରଣତ ,, ASCII କୋଡ୍ ପରି ଅକ୍ଷରଗୁଡିକର ଏକ ଷ୍ଟ୍ରିଙ୍ଗ୍ ଯେପରିକି "ହେଲୋ ସେଠାରେ" ଶବ୍ଦଗୁଡିକ ପ୍ରତି ଅକ୍ଷର ପ୍ରତି ନିର୍ଦ୍ଦିଷ୍ଟ ସଂଖ୍ୟକ ବିଟ୍ ବ୍ୟବହାର କରି ଉପସ୍ଥାପିତ ହୁଏ | ଯେତେବେଳେ ଏକ ଷ୍ଟ୍ରିଙ୍ଗ୍ ଆରିଥମେଟିକ୍ ଏନକୋଡିଂରେ ରୂପାନ୍ତରିତ ହୁଏ, ବାରମ୍ବାର ବ୍ୟବହୃତ ଅକ୍ଷରଗୁଡ଼ିକ କମ୍ ବିଟ୍ ସହିତ ଗଚ୍ଛିତ ହେବ ଏବଂ ବାରମ୍ବାର ଘଟୁଥିବା ଅକ୍ଷରଗୁଡିକ ଅଧିକ ବିଟ୍ ସହିତ ଗଚ୍ଛିତ ହେବ, ଫଳସ୍ୱରୂପ ସମୁଦାୟ ବ୍ୟବହୃତ କମ୍ ବିଟ୍ | ଆରିଥମେଟିକ୍ କୋଡିଂ ଅନ୍ୟ ପ୍ରକାର ଏଣ୍ଟ୍ରପି ଏନକୋଡିଂ ଠାରୁ ଭିନ୍ନ, ଯେପରିକି ହଫମାନ କୋଡିଂ, ଏଥିରେ ଇନପୁଟକୁ ଉପାଦାନ ସଙ୍କେତରେ ପୃଥକ କରିବା ଏବଂ ପ୍ରତ୍ୟେକକୁ ଏକ କୋଡ୍ ସହିତ ବଦଳାଇବା ପରିବର୍ତ୍ତେ, ଆରିଥମେଟିକ୍ କୋଡିଂ ସମଗ୍ର ସନ୍ଦେଶକୁ ଏକ ନମ୍ବରରେ ଏନକୋଡ୍ କରେ, ଏକ ଇଚ୍ଛାଧୀନ-ସଠିକତା ଭଗ୍ନାଂଶ q ଯେଉଁଠାରେ 0.0 ≤ q <1.0। ଏହା ସାମ୍ପ୍ରତିକ ସୂଚନାକୁ ଏକ ପରିସର ଭାବରେ ଦର୍ଶାଏ, ଦୁଇଟି ସଂଖ୍ୟା ଦ୍ୱାରା ବ୍ୟାଖ୍ୟା କରାଯାଇଛି | ଅସୀମେଟ୍ରିକ୍ ସାଂଖ୍ୟିକ ପ୍ରଣାଳୀ ନାମକ ଏକ ଏଣ୍ଟ୍ରପି କୋଡର୍ ର ଏକ ପରିବାର ବର୍ତ୍ତମାନର ସୂଚନାକୁ ପ୍ରତିନିଧିତ୍ୱ କରୁଥିବା ଏକ ପ୍ରାକୃତିକ ସଂଖ୍ୟାରେ ସିଧାସଳଖ କାର୍ଯ୍ୟ କରିଥିବାରୁ ଶୀଘ୍ର କାର୍ଯ୍ୟକାରିତା ପାଇଁ ଅନୁମତି ଦେଇଥାଏ |
ଅଭିବ୍ୟକ୍ତି (ଗଣିତ): ଗଣିତରେ, ଏକ ଅଭିବ୍ୟକ୍ତି ବା ଗାଣିତିକ ଅଭିବ୍ୟକ୍ତି ହେଉଛି ପ୍ରତୀକଗୁଡ଼ିକର ଏକ ସୀମିତ ମିଶ୍ରଣ ଯାହା ପ୍ରସଙ୍ଗ ଉପରେ ନିର୍ଭର କରୁଥିବା ନିୟମ ଅନୁଯାୟୀ ଭଲ ଭାବରେ ଗଠିତ | ଗାଣିତିକ ପ୍ରତୀକଗୁଡ଼ିକ ସଂଖ୍ୟା (ସ୍ଥିର), ଭେରିଏବଲ୍, ଅପରେସନ୍, ଫଙ୍କସନ୍, ବ୍ରାକେଟ୍, ବିରାମଚିହ୍ନ, ଏବଂ ଗ୍ରୁପିଂକୁ ଅପରେସନ୍ କ୍ରମ ଏବଂ ଲଜିକାଲ୍ ସିଣ୍ଟାକ୍ସର ଅନ୍ୟାନ୍ୟ ଦିଗ ନିର୍ଣ୍ଣୟ କରିବାରେ ସାହାଯ୍ୟ କରିପାରିବ |
ପିତାମାତାମାନଙ୍କ ପାଇଁ ଗାଣିତିକ: ପିତାମାତାମାନେ ପାଇଁ ଗାଣିତିକ aimed ପିତାମାତା ଓ ଶିକ୍ଷକ ରେ ଗଣିତ ଶିକ୍ଷା ବିଷୟରେ ଏକ ପୁସ୍ତକ ଅଟେ।
ପିତାମାତାମାନଙ୍କ ପାଇଁ ଗାଣିତିକ: ପିତାମାତାମାନେ ପାଇଁ ଗାଣିତିକ aimed ପିତାମାତା ଓ ଶିକ୍ଷକ ରେ ଗଣିତ ଶିକ୍ଷା ବିଷୟରେ ଏକ ପୁସ୍ତକ ଅଟେ।
କଦଳୀ ଆକ୍ସୋମସ୍: ଗାଣିତିକ ତର୍କ ରେ, Peano axioms, Dedekind-Peano axioms କିମ୍ବା Peano postulates ଭାବରେ ଜଣା ପ୍ରାକୃତିକ ସଂଖ୍ୟା 19 ଶତାବ୍ଦୀ ଇଟାଲୀୟ ଗଣିତଜ୍ଞ Giuseppe Peano ଦ୍ଵାରା ଉପସ୍ଥାପିତ ପାଇଁ axioms, ଅଟନ୍ତି। ସଂଖ୍ୟା କିମ୍ବା ପ୍ରତୀକ ସହିତ ଅକ୍ଷର ମଧ୍ଯ ବ୍ୟବହାର କରି।
ଭଗ୍ନାଂଶ: ଏକ ଭଗ୍ନାଂଶ ସମୁଦାୟର ଏକ ଅଂଶକୁ ପ୍ରତିନିଧିତ୍ୱ କରେ କିମ୍ବା ସାଧାରଣତ any ଯେକ any ଣସି ସଂଖ୍ୟକ ସମାନ ଅଂଶକୁ ପ୍ରତିନିଧିତ୍ୱ କରେ | ଯେତେବେଳେ ଦ day ନନ୍ଦିନ ଇଂରାଜୀରେ କଥାବାର୍ତ୍ତା ହୁଏ, ଏକ ଭଗ୍ନାଂଶ ବର୍ଣ୍ଣନା କରେ ଯେ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଆକାରର କେତେ ଅଂଶ ଅଛି, ଉଦାହରଣ ସ୍ୱରୂପ, ଦେ half ଼, ଆଠ-ପଞ୍ଚମାଂଶ, ତିନି-ଚତୁର୍ଥାଂଶ | ଏକ ସାଧାରଣ, ସାଧାରଣ, କିମ୍ବା ସରଳ ଭଗ୍ନାଂଶ ଏକ ଲବ ଗଠିତ, ଏକ ଧାଡି ଉପରୋକ୍ତ ପ୍ରଦର୍ଶିତ ଏବଂ ଏକ ଅଣ-ଶୂନ ହର, ସେହି ଧାଡି ତଳେ ପ୍ରଦର୍ଶିତ। ଭଗ୍ନାଂଶରେ ଗଣନାକାରୀ ଏବଂ ନାମକରଣ ମଧ୍ୟ ବ୍ୟବହୃତ ହୁଏ ଯାହା ସାଧାରଣ ନୁହେଁ , ଯ comp ଗିକ ଭଗ୍ନାଂଶ, ଜଟିଳ ଭଗ୍ନାଂଶ ଏବଂ ମିଶ୍ରିତ ସଂଖ୍ୟା ସହିତ |
ଗାଣିତିକ କାର୍ଯ୍ୟ: ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତରେ, ଏକ ଗାଣିତିକ , ଗାଣିତିକ , କିମ୍ବା ସଂଖ୍ୟା-ତତ୍ତ୍ୱିକ କାର୍ଯ୍ୟ ଅଧିକାଂଶ ଲେଖକଙ୍କ ପାଇଁ ଯେକ any ଣସି କାର୍ଯ୍ୟ f ( n ) ଯାହାର ଡୋମେନ୍ ସକରାତ୍ମକ ପୂର୍ଣ୍ଣ ସଂଖ୍ୟା ଏବଂ ଯାହାର ପରିସର ଜଟିଳ ସଂଖ୍ୟାଗୁଡ଼ିକର ଉପସେଟ ଅଟେ | ହାର୍ଡି ଏବଂ ରାଇଟ୍ ସେମାନଙ୍କର ପରିଭାଷାରେ ଆବଶ୍ୟକତାକୁ ଅନ୍ତର୍ଭୁକ୍ତ କରନ୍ତି ଯେ ଏକ ଗାଣିତିକ କାର୍ଯ୍ୟ " n ର କିଛି ଗାଣିତିକ ଗୁଣ ପ୍ରକାଶ କରେ" |
ଗାଣିତିକ କାର୍ଯ୍ୟ: ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତରେ, ଏକ ଗାଣିତିକ , ଗାଣିତିକ , କିମ୍ବା ସଂଖ୍ୟା-ତତ୍ତ୍ୱିକ କାର୍ଯ୍ୟ ଅଧିକାଂଶ ଲେଖକଙ୍କ ପାଇଁ ଯେକ any ଣସି କାର୍ଯ୍ୟ f ( n ) ଯାହାର ଡୋମେନ୍ ସକରାତ୍ମକ ପୂର୍ଣ୍ଣ ସଂଖ୍ୟା ଏବଂ ଯାହାର ପରିସର ଜଟିଳ ସଂଖ୍ୟାଗୁଡ଼ିକର ଉପସେଟ ଅଟେ | ହାର୍ଡି ଏବଂ ରାଇଟ୍ ସେମାନଙ୍କର ପରିଭାଷାରେ ଆବଶ୍ୟକତାକୁ ଅନ୍ତର୍ଭୁକ୍ତ କରନ୍ତି ଯେ ଏକ ଗାଣିତିକ କାର୍ଯ୍ୟ " n ର କିଛି ଗାଣିତିକ ଗୁଣ ପ୍ରକାଶ କରେ" |
ଗାଣିତିକ ବଂଶ: ଗଣିତରେ, ଏକ ବୀଜ ବର୍ଣ୍ଣିତ ପ୍ରକାରର ଆରିଥମେଟିକ୍ ଜେନସ୍ ହେଉଛି ଏକ ବୀଜ ବର୍ଣ୍ଣିତ ବକ୍ର କିମ୍ବା ରିମାନ୍ ପୃଷ୍ଠର ବଂଶର କିଛି ସମ୍ଭାବ୍ୟ ସାଧାରଣକରଣ ମଧ୍ୟରୁ ଗୋଟିଏ |
ଗାଣିତିକ - ଜ୍ୟାମିତିକ ଅର୍ଥ: ଗଣିତରେ, ଦୁଇଟି ସକାରାତ୍ମକ ପ୍ରକୃତ ସଂଖ୍ୟା x ଏବଂ y ର ଗାଣିତିକ - ଜ୍ୟାମିତିକ ଅର୍ଥ ( AGM ) କୁ ନିମ୍ନଲିଖିତ ଭାବରେ ବ୍ୟାଖ୍ୟା କରାଯାଇଛି:
ଗାଣିତିକ ଜ୍ୟାମିତି: ଗଣିତରେ, ଗାଣିତିକ ଜ୍ୟାମିତି ପ୍ରାୟତ al ବୀଜ ବର୍ଣ୍ଣିତ ଜ୍ୟାମିତିରୁ ସଂଖ୍ୟା ତତ୍ତ୍ problems ର ସମସ୍ୟା ପର୍ଯ୍ୟନ୍ତ କ techni ଶଳର ପ୍ରୟୋଗ ଅଟେ | ଆରିଥମେଟିକ୍ ଜ୍ୟାମିତ୍ରୀ ଡାୟୋଫାଣ୍ଟାଇନ୍ ଜ୍ୟାମିତିର ଚାରିପାଖରେ କେନ୍ଦ୍ରୀଭୂତ ହୋଇଛି, ବୀଜ ବର୍ଣ୍ଣିତ କିସମର ଯୁକ୍ତିଯୁକ୍ତ ବିନ୍ଦୁ ଅଧ୍ୟୟନ |
ଗାଣିତିକ ଗୋଷ୍ଠୀ: ଗଣିତରେ, ଏକ ଗାଣିତିକ ଗୋଷ୍ଠୀ ହେଉଛି ଏକ ଗୋଷ୍ଠୀ ଯାହାକି ଏକ ବୀଜ ବର୍ଣ୍ଣିତ ଗୋଷ୍ଠୀର ପୂର୍ଣ୍ଣ ପଏଣ୍ଟ ଭାବରେ ପ୍ରାପ୍ତ ହୋଇଛି | ଚତୁର୍ଥାଂଶ ଫର୍ମଗୁଡିକର ଗାଣିତିକ ଗୁଣ ଏବଂ ସଂଖ୍ୟା ତତ୍ତ୍ other ରେ ଅନ୍ୟାନ୍ୟ ଶାସ୍ତ୍ରୀୟ ବିଷୟଗୁଡିକ ଅଧ୍ୟୟନରେ ସେମାନେ ସ୍ natural ାଭାବିକ ଭାବରେ ଉଭା ହୁଅନ୍ତି | ସେମାନେ ରିମାନିଆନ୍ ମେନିଫୋଲ୍ଡର ଅତି ଆକର୍ଷଣୀୟ ଉଦାହରଣ ମଧ୍ୟ ସୃଷ୍ଟି କରନ୍ତି ଏବଂ ତେଣୁ ଭିନ୍ନ ଭିନ୍ନ ଜ୍ୟାମିତି ଏବଂ ଟପୋଲୋଜି ପ୍ରତି ଆଗ୍ରହର ବିଷୟ | ଶେଷରେ, ଏହି ଦୁଇଟି ବିଷୟ ଅଟୋମୋର୍ଫିକ୍ ଫର୍ମଗୁଡିକର ସିଦ୍ଧାନ୍ତରେ ଯୋଗଦାନ କରେ ଯାହା ଆଧୁନିକ ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତରେ ମ fundamental ଳିକ ଅଟେ |
ରେଖା କାର୍ଯ୍ୟ: ଗଣିତରେ, ର line ଖ୍ୟ କାର୍ଯ୍ୟ ଶବ୍ଦ ଦୁଇଟି ଭିନ୍ନ କିନ୍ତୁ ସମ୍ବନ୍ଧୀୟ ଧାରଣାକୁ ବୁ refers ାଏ: କାଲ୍କୁଲସ୍ ଏବଂ ଆନୁଷଙ୍ଗିକ କ୍ଷେତ୍ରରେ, ଏକ ର ar ଖ୍ୟ କାର୍ଯ୍ୟ ହେଉଛି ଏକ କାର୍ଯ୍ୟ, ଯାହାର ଗ୍ରାଫ୍ ଏକ ସିଧା ଲାଇନ, ଅର୍ଥାତ୍ ଡିଗ୍ରୀ ଶୂନ୍ୟର ଏକ ବହୁଜନିଆ କାର୍ଯ୍ୟ | ଅନ୍ୟ ଧାରଣା ଠାରୁ ଏହିପରି ଏକ ର ar ଖ୍ୟ କାର୍ଯ୍ୟକୁ ପୃଥକ କରିବା ପାଇଁ ଆଫାଇନ୍ ଫଙ୍କସନ୍ ଶବ୍ଦ ପ୍ରାୟତ used ବ୍ୟବହୃତ ହୁଏ | ର line ଖ୍ୟ ବୀଜ ବିବେଚନା, ଗାଣିତିକ ବିଶ୍ଳେଷଣ ଏବଂ କାର୍ଯ୍ୟକଳାପ ବିଶ୍ଳେଷଣରେ, ଏକ ର ar ଖ୍ୟ କାର୍ଯ୍ୟ ହେଉଛି ଏକ ର ar ଖ୍ୟ ମାନଚିତ୍ର |
ଜ୍ୟାମିତିକ ଅର୍ଥ: ଗଣିତରେ, ଜ୍ୟାମିତିକ ଅର୍ଥ ହେଉଛି ଏକ ହାରାହାରି ବା ହାରାହାରି, ଯାହା ସେମାନଙ୍କର ମୂଲ୍ୟର ଉତ୍ପାଦ ବ୍ୟବହାର କରି ସଂଖ୍ୟାଗୁଡ଼ିକର ଏକ ସେଟ୍ ର କେନ୍ଦ୍ରୀୟ ପ୍ରବୃତ୍ତି କିମ୍ବା ସାଧାରଣ ମୂଲ୍ୟକୁ ସୂଚିତ କରେ | ଜ୍ୟାମିତିକ ଅର୍ଥ n ସଂଖ୍ୟାର ଉତ୍ପାଦର n th ମୂଳ ଭାବରେ ବ୍ୟାଖ୍ୟା କରାଯାଇଛି, ଅର୍ଥାତ୍ x 1 , x 2 , ..., x n ସଂଖ୍ୟାଗୁଡ଼ିକର ଏକ ସେଟ୍ ପାଇଁ, ଜ୍ୟାମିତିକ ଅର୍ଥ ପରି ବ୍ୟାଖ୍ୟା କରାଯାଇଛି |
ଗାଣିତିକ କ୍ରମ: ଗାଣିତିକ ତର୍କ ରେ, arithmetical ଅନୁକ୍ରମ, ଗାଣିତିକ ଅନୁକ୍ରମ କିମ୍ବା Kleene-Mostowski ଅନୁକ୍ରମ ସେମାନଙ୍କୁ ବ୍ୟାଖ୍ୟା ଯେ ସୂତ୍ର ଜଟିଳତାକୁ ଉପରେ ଆଧାରିତ ନିର୍ଦ୍ଦିଷ୍ଟ େସଟଗୁଡ଼ିକ classifies। ଯେକ Any ଣସି ସେଟ୍ ଯାହା ଏକ ଶ୍ରେଣୀକରଣ ଗ୍ରହଣ କରେ ଏହାକୁ ଗଣିତ କୁହାଯାଏ |
ଗାଣିତିକ ହାଇପରବୋଲିକ୍ 3-ଗୁଣ: ଗଣିତରେ, ସଠିକ୍ ଭାବରେ ଗୋଷ୍ଠୀ ସିଦ୍ଧାନ୍ତ ଏବଂ ହାଇପରବୋଲିକ୍ ଜ୍ୟାମିତ୍ରୀରେ , ଆରିଥମେଟିକ୍ କ୍ଲିନିଆନ୍ ଗୋଷ୍ଠୀଗୁଡିକ କ୍ୱାଟର୍ନିଅନ୍ ବୀଜ ବର୍ଣ୍ଣରେ ଅର୍ଡର ବ୍ୟବହାର କରି ନିର୍ମିତ କ୍ଲିନିଆନ୍ ଗୋଷ୍ଠୀର ଏକ ସ୍ୱତନ୍ତ୍ର ଶ୍ରେଣୀ | ସେମାନେ ଗାଣିତିକ ଗୋଷ୍ଠୀର ନିର୍ଦ୍ଦିଷ୍ଟ ଉଦାହରଣ | ଏକ ଆରିଥମେଟିକ୍ ହାଇପରବୋଲିକ୍ ଥ୍ରୀ-ମେନିଫୋଲ୍ଡ ହେଉଛି ହାଇପରବୋଲିକ୍ ସ୍ପେସ୍ ର କୋଟୋଏଣ୍ଟ୍ | ଏକ ଗାଣିତିକ କ୍ଲିନିଆନ୍ ଗୋଷ୍ଠୀ ଦ୍ୱାରା | ଏହି ମେନିଫୋଲ୍ଡଗୁଡ଼ିକରେ କିଛି ବିଶେଷ ସୁନ୍ଦର ବା ଉଲ୍ଲେଖନୀୟ ଉଦାହରଣ ଅନ୍ତର୍ଭୁକ୍ତ |
ଗାଣିତିକ ଫୁଚିଆନ୍ ଗୋଷ୍ଠୀ: ଆରିଥମେଟିକ୍ ଫୁଚିଆନ୍ ଗୋଷ୍ଠୀଗୁଡ଼ିକ ହେଉଛି କ୍ୱାଟର୍ନିଅନ୍ ଆଲଜେବ୍ରାରେ ଅର୍ଡର ବ୍ୟବହାର କରି ନିର୍ମିତ ଫୁଚିଆନ୍ ଗୋଷ୍ଠୀର ଏକ ସ୍ୱତନ୍ତ୍ର ଶ୍ରେଣୀ | ସେମାନେ ଗାଣିତିକ ଗୋଷ୍ଠୀର ନିର୍ଦ୍ଦିଷ୍ଟ ଉଦାହରଣ | ଏକ ଗାଣିତିକ ଫୁଚିଆନ୍ ଗୋଷ୍ଠୀର ପ୍ରୋଟୋଟାଇପିକାଲ୍ ଉଦାହରଣ ହେଉଛି ମଡ୍ୟୁଲାର୍ ଗ୍ରୁପ୍ | । ସେମାନେ, ଏବଂ ହାଇପରବୋଲିକ୍ ପୃଷ୍ଠରେ ସେମାନଙ୍କର କାର୍ଯ୍ୟ ସହିତ ଜଡିତ ହାଇପରବୋଲିକ୍ ପୃଷ୍ଠ ପ୍ରାୟତ Fu ଫୁଚିଆନ୍ ଗୋଷ୍ଠୀ ଏବଂ ହାଇପରବୋଲିକ୍ ପୃଷ୍ଠଗୁଡ଼ିକ ମଧ୍ୟରେ ନିୟମିତ ଆଚରଣ ପ୍ରଦର୍ଶନ କରେ |
ଗାଣିତିକ IF: ଆରିଥମେଟିକ୍ IF ଷ୍ଟେଟମେଣ୍ଟ ହେଉଛି ଏକ ତିନି-ମାର୍ଗ ଗଣିତ କଣ୍ଡିଶନାଲ୍ ଷ୍ଟେଟମେଣ୍ଟ, ପ୍ରଥମେ 1957 ରେ ଫୋର୍ଟ୍ରାନ୍ ର ପ୍ରଥମ ପ୍ରକାଶନରେ ଦେଖାଯାଇଥିଲା ଏବଂ ପରବର୍ତ୍ତୀ ସଂସ୍କରଣରେ ଏବଂ ଅନ୍ୟାନ୍ୟ ପ୍ରୋଗ୍ରାମିଂ ଭାଷା ଯେପରିକି FOCAL | ଅନ୍ୟ ଭାଷାରେ ଦେଖାଯାଇଥିବା ଯୁକ୍ତିଯୁକ୍ତ IF ଷ୍ଟେଟମେଣ୍ଟ ପରି, ଫୋର୍ଟ୍ରାନ୍ ଷ୍ଟେଟମେଣ୍ଟ୍ ତିନୋଟି ଭିନ୍ନ ଶାଖାକୁ ବ୍ୟାଖ୍ୟା କରେ ଯାହା ଉପରେ ନିର୍ଭର କରି ଏକ ଅଭିବ୍ୟକ୍ତିର ଫଳାଫଳ ନକାରାତ୍ମକ, ଶୂନ୍ୟ କିମ୍ବା ସକରାତ୍ମକ ଅଟେ:
ଗଣିତ କଳା ଉପରେ ନଅ ଅଧ୍ୟାୟ: ଗଣିତ କଳା ଉପରେ ନଅ ଅଧ୍ୟାୟ ହେଉଛି ଏକ ଚାଇନାର ଗଣିତ ପୁସ୍ତକ, ଯାହା ଖ୍ରୀଷ୍ଟପୂର୍ବ ଦଶମ - ଦ୍ century ିତୀୟ ଶତାବ୍ଦୀର ପଣ୍ଡିତମାନଙ୍କ ଦ୍ୱାରା ରଚନା କରାଯାଇଥିଲା, ଏହାର ଶେଷ ପର୍ଯ୍ୟାୟ ଦ୍ୱିତୀୟ ଶତାବ୍ଦୀରୁ ହୋଇଥିଲା | ଏହି ପୁସ୍ତକ ଚାଇନାରୁ ସର୍ବପ୍ରଥମ ବଞ୍ଚିଥିବା ଗାଣିତିକ ଗ୍ରନ୍ଥ ମଧ୍ୟରୁ ଅନ୍ୟତମ, ସୁଆନ୍ ଶୁ ଶୁ ଏବଂ ଜୋବି ସୁଆଜିଙ୍ଗ୍ | ଏହା ଗଣିତ ପାଇଁ ଏକ ପନ୍ଥା ଅବଲମ୍ବନ କରେ ଯାହା ସମସ୍ୟାର ସମାଧାନର ସାଧାରଣ ପଦ୍ଧତି ଖୋଜିବା ଉପରେ ଧ୍ୟାନ ଦେଇଥାଏ, ଯାହା ପ୍ରାଚୀନ ଗ୍ରୀକ୍ ଗଣିତଜ୍ଞଙ୍କ ପାଇଁ ସାଧାରଣ ଆଭିମୁଖ୍ୟ ସହିତ ଭିନ୍ନ ହୋଇପାରେ, ଯେଉଁମାନେ ଆକ୍ସିୟୋମର ପ୍ରାରମ୍ଭିକ ସେଟରୁ ପ୍ରସ୍ତାବ ବାହାର କରିବାକୁ ଚେଷ୍ଟା କରିଥିଲେ |
ସୀମିତ କ୍ଷେତ୍ର ଗଣିତ: ଗଣିତରେ, ସୀମିତ କ୍ଷେତ୍ର ଆରିଥମେଟିକ୍ ଏକ ସୀମିତ କ୍ଷେତ୍ରରେ ଗାଣିତିକ ଅଟେ ଯାହା ଯୁକ୍ତିଯୁକ୍ତ ସଂଖ୍ୟା କ୍ଷେତ୍ର ପରି ଏକ ଅସୀମ ସଂଖ୍ୟକ ଉପାଦାନ ସହିତ ଏକ କ୍ଷେତ୍ରରେ ଗଣିତର ବିପରୀତ ଅଟେ |
ଗଣିତ କଳା ଉପରେ ନଅ ଅଧ୍ୟାୟ: ଗଣିତ କଳା ଉପରେ ନଅ ଅଧ୍ୟାୟ ହେଉଛି ଏକ ଚାଇନାର ଗଣିତ ପୁସ୍ତକ, ଯାହା ଖ୍ରୀଷ୍ଟପୂର୍ବ ଦଶମ - ଦ୍ century ିତୀୟ ଶତାବ୍ଦୀର ପଣ୍ଡିତମାନଙ୍କ ଦ୍ୱାରା ରଚନା କରାଯାଇଥିଲା, ଏହାର ଶେଷ ପର୍ଯ୍ୟାୟ ଦ୍ୱିତୀୟ ଶତାବ୍ଦୀରୁ ହୋଇଥିଲା | ଏହି ପୁସ୍ତକ ଚାଇନାରୁ ସର୍ବପ୍ରଥମ ବଞ୍ଚିଥିବା ଗାଣିତିକ ଗ୍ରନ୍ଥ ମଧ୍ୟରୁ ଅନ୍ୟତମ, ସୁଆନ୍ ଶୁ ଶୁ ଏବଂ ଜୋବି ସୁଆଜିଙ୍ଗ୍ | ଏହା ଗଣିତ ପାଇଁ ଏକ ପନ୍ଥା ଅବଲମ୍ବନ କରେ ଯାହା ସମସ୍ୟାର ସମାଧାନର ସାଧାରଣ ପଦ୍ଧତି ଖୋଜିବା ଉପରେ ଧ୍ୟାନ ଦେଇଥାଏ, ଯାହା ପ୍ରାଚୀନ ଗ୍ରୀକ୍ ଗଣିତଜ୍ଞଙ୍କ ପାଇଁ ସାଧାରଣ ଆଭିମୁଖ୍ୟ ସହିତ ଭିନ୍ନ ହୋଇପାରେ, ଯେଉଁମାନେ ଆକ୍ସିୟୋମର ପ୍ରାରମ୍ଭିକ ସେଟରୁ ପ୍ରସ୍ତାବ ବାହାର କରିବାକୁ ଚେଷ୍ଟା କରିଥିଲେ |
ଛାତର ମଡେଲ୍: ରୁଫ୍ ଲାଇନ୍ ମଡେଲ୍ ହେଉଛି ଏକ ଅନ୍ତର୍ନିହିତ ଭିଜୁଆଲ୍ କାର୍ଯ୍ୟଦକ୍ଷତା ମଡେଲ୍, ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ କମ୍ପ୍ୟୁଟ କର୍ଣ୍ଣଲ କିମ୍ବା ମଲ୍ଟି-କୋର, ବହୁ-କୋର, କିମ୍ବା ତ୍ୱରାନ୍ୱିତ ପ୍ରୋସେସର୍ ସ୍ଥାପତ୍ୟରେ ଚାଲୁଥିବା ପ୍ରୟୋଗର କାର୍ଯ୍ୟଦକ୍ଷତା ଆକଳନ ପ୍ରଦାନ କରିବା ପାଇଁ ବ୍ୟବହୃତ ହୁଏ, ଅନ୍ତର୍ନିହିତ ହାର୍ଡୱେର୍ ସୀମିତତା, ଏବଂ ସମ୍ଭାବ୍ୟ ଲାଭ ଏବଂ ଅପ୍ଟିମାଇଜେସନ୍ ର ପ୍ରାଥମିକତା | ସ୍ଥାନୀୟତା, ବ୍ୟାଣ୍ଡୱିଡଥ୍, ଏବଂ ବିଭିନ୍ନ ସମାନ୍ତରାଳ ପାରାଡିଗମକୁ ଏକ କାର୍ଯ୍ୟଦକ୍ଷତା ଚିତ୍ରରେ ମିଶ୍ରଣ କରି, ମଡେଲ୍ ସରଳ ଶତକଡ଼ା-ଶିଖର ଆକଳନ ବ୍ୟବହାର କରିବା ପରିବର୍ତ୍ତେ ପ୍ରାପ୍ତ କାର୍ଯ୍ୟର ଗୁଣବତ୍ତା ଆକଳନ କରିବା ପାଇଁ ଏକ ପ୍ରଭାବଶାଳୀ ବିକଳ୍ପ ହୋଇପାରେ, ଯେହେତୁ ଏହା ଉଭୟ କାର୍ଯ୍ୟକାରିତା ଉପରେ ଅନ୍ତର୍ନିହିତ ସୂଚନା ପ୍ରଦାନ କରିଥାଏ | ଅନ୍ତର୍ନିହିତ କାର୍ଯ୍ୟଦକ୍ଷତା ସୀମିତତା |
ବହୁଗୁଣ ଓଲଟା: ଗଣିତ, ଏକ multiplicative inverse କିମ୍ବା ପାରସ୍ପରିକ ଏକ ସଂଖ୍ୟା X ପାଇଁ, ଦ୍ୱାରା 1 / x କିମ୍ବା x -1, ଏକ ସଂଖ୍ୟା ଯାହା ଯେତେବେଳେ x ଦ୍ୱାରା ବୃଦ୍ଧି multiplicative ପରିଚୟ, 1. ଏକ ଭଗ୍ନାଂଶ ଏକ ର multiplicative inverse / b ହେଉଛି b ନିଜେ ହେଉଛି / ଅବଧାରଣା a । ଏକ ପ୍ରକୃତ ସଂଖ୍ୟାର ଗୁଣାତ୍ମକ ଓଲଟା ପାଇଁ, ସଂଖ୍ୟା ଦ୍ୱାରା 1 ଭାଗ କରନ୍ତୁ | ଉଦାହରଣ ସ୍ୱରୂପ, 5 ର ପ୍ରତିକ୍ରିୟା ଏକ ପ fifth ୍ଚମ, ଏବଂ 0.25 ର ପ୍ରତିକ୍ରିୟା 1 କୁ 0.25, କିମ୍ବା 4 ଦ୍ divided ାରା ବିଭକ୍ତ କରାଯାଇଛି | ପ୍ରତିକ୍ରିୟାତ୍ମକ କାର୍ଯ୍ୟ , ଫଙ୍କସନ୍ f ( x ) ଯାହା x ରୁ 1 / x ମାନଚିତ୍ର କରେ, ଏହାର ଏକ ସରଳ ଉଦାହରଣ ଅଟେ | ଏକ ଫଙ୍କସନ୍ ଯାହା ଏହାର ଓଲଟା ଅଟେ |
ଲାଟାଇସ୍ (ପୃଥକ ଉପଗୋଷ୍ଠୀ): ମିଛ ତତ୍ତ୍ and ଏବଂ ଗଣିତର ଆନୁସଙ୍ଗିକ କ୍ଷେତ୍ରରେ, ଏକ ସ୍ଥାନୀୟ କମ୍ପାକ୍ଟ ଗୋଷ୍ଠୀର ଏକ ଲାଟାଇସ୍ ହେଉଛି ସମ୍ପତ୍ତି ସହିତ ଏକ ପୃଥକ ଉପଗୋଷ୍ଠୀ ଯାହା କ୍ୱିଣ୍ଟେଣ୍ଟ୍ ସ୍ପେସ୍ ସୀମିତ ଇନଭାରିଅଣ୍ଟ୍ ମାପ ଅଟେ | R n ର ଉପଗୋଷ୍ଠୀଗୁଡିକର ସ୍ case ତନ୍ତ୍ର କ୍ଷେତ୍ରରେ, ଏହା ପଏଣ୍ଟର ପର୍ଯ୍ୟାୟ ସବସେଟ୍ ଭାବରେ ଏକ ଲାଟାଇସର ସାଧାରଣ ଜ୍ୟାମିତିକ ଧାରଣା ସହିତ ପରିଣତ ହୁଏ, ଏବଂ ଲାଟାଇସର ଉଭୟ ବୀଜ ବର୍ଣ୍ଣିତ ଗଠନ ଏବଂ ସମସ୍ତ ଲାଟାଇଟ୍ ସ୍ପେସ୍ ର ଜ୍ୟାମିତି ଅପେକ୍ଷାକୃତ ଭଲ ଭାବରେ ବୁ understood ାପଡେ |