Arithmetic logic unit, Arithmetic logic unit, Arithmetic logic unit

ଗାଣିତିକ ତର୍କ ଏକକ: ଗଣନାରେ, ଏକ ଆରିଥମେଟିକ୍ ଲଜିକ୍ ୟୁନିଟ୍ (ALU) ହେଉଛି ଏକ ମିଳିତ ଡିଜିଟାଲ୍ ସର୍କିଟ୍ ଯାହା ଇଣ୍ଟିଜର୍ ବାଇନାରୀ ନମ୍ବର ଉପରେ ଗାଣିତିକ ଏବଂ ବିଟୱାଇସ୍ ଅପରେସନ୍ କରିଥାଏ | ଏହା ଏକ ଫ୍ଲୋଟିଂ ପଏଣ୍ଟ ୟୁନିଟ୍ (FPU) ର ବିପରୀତ, ଯାହା ଫ୍ଲୋଟିଂ ପଏଣ୍ଟ ନମ୍ବର ଉପରେ କାର୍ଯ୍ୟ କରେ | ଏହା କମ୍ପ୍ୟୁଟର, FPU ଏବଂ ଗ୍ରାଫିକ୍ସ ପ୍ରକ୍ରିୟାକରଣ ୟୁନିଟ୍ (ଜିପିୟୁ) ର କେନ୍ଦ୍ରୀୟ ପ୍ରକ୍ରିୟାକରଣ ୟୁନିଟ୍ (CPU) ଅନ୍ତର୍ଭୂକ୍ତ କରି ଅନେକ ପ୍ରକାରର ଗଣନା ସର୍କିଟ୍ ର ଏକ ମ fundamental ଳିକ ବିଲ୍ଡିଂ ବ୍ଲକ୍ |
ଗାଣିତିକ ତର୍କ ଏକକ: ଗଣନାରେ, ଏକ ଆରିଥମେଟିକ୍ ଲଜିକ୍ ୟୁନିଟ୍ (ALU) ହେଉଛି ଏକ ମିଳିତ ଡିଜିଟାଲ୍ ସର୍କିଟ୍ ଯାହା ଇଣ୍ଟିଜର୍ ବାଇନାରୀ ନମ୍ବର ଉପରେ ଗାଣିତିକ ଏବଂ ବିଟୱାଇସ୍ ଅପରେସନ୍ କରିଥାଏ | ଏହା ଏକ ଫ୍ଲୋଟିଂ ପଏଣ୍ଟ ୟୁନିଟ୍ (FPU) ର ବିପରୀତ, ଯାହା ଫ୍ଲୋଟିଂ ପଏଣ୍ଟ ନମ୍ବର ଉପରେ କାର୍ଯ୍ୟ କରେ | ଏହା କମ୍ପ୍ୟୁଟର, FPU ଏବଂ ଗ୍ରାଫିକ୍ସ ପ୍ରକ୍ରିୟାକରଣ ୟୁନିଟ୍ (ଜିପିୟୁ) ର କେନ୍ଦ୍ରୀୟ ପ୍ରକ୍ରିୟାକରଣ ୟୁନିଟ୍ (CPU) ଅନ୍ତର୍ଭୂକ୍ତ କରି ଅନେକ ପ୍ରକାରର ଗଣନା ସର୍କିଟ୍ ର ଏକ ମ fundamental ଳିକ ବିଲ୍ଡିଂ ବ୍ଲକ୍ |
ଗାଣିତିକ ତର୍କ ଏକକ: ଗଣନାରେ, ଏକ ଆରିଥମେଟିକ୍ ଲଜିକ୍ ୟୁନିଟ୍ (ALU) ହେଉଛି ଏକ ମିଳିତ ଡିଜିଟାଲ୍ ସର୍କିଟ୍ ଯାହା ଇଣ୍ଟିଜର୍ ବାଇନାରୀ ନମ୍ବର ଉପରେ ଗାଣିତିକ ଏବଂ ବିଟୱାଇସ୍ ଅପରେସନ୍ କରିଥାଏ | ଏହା ଏକ ଫ୍ଲୋଟିଂ ପଏଣ୍ଟ ୟୁନିଟ୍ (FPU) ର ବିପରୀତ, ଯାହା ଫ୍ଲୋଟିଂ ପଏଣ୍ଟ ନମ୍ବର ଉପରେ କାର୍ଯ୍ୟ କରେ | ଏହା କମ୍ପ୍ୟୁଟର, FPU ଏବଂ ଗ୍ରାଫିକ୍ସ ପ୍ରକ୍ରିୟାକରଣ ୟୁନିଟ୍ (ଜିପିୟୁ) ର କେନ୍ଦ୍ରୀୟ ପ୍ରକ୍ରିୟାକରଣ ୟୁନିଟ୍ (CPU) ଅନ୍ତର୍ଭୂକ୍ତ କରି ଅନେକ ପ୍ରକାରର ଗଣନା ସର୍କିଟ୍ ର ଏକ ମ fundamental ଳିକ ବିଲ୍ଡିଂ ବ୍ଲକ୍ |
ପାସ୍କାଲର କାଲକୁଲେଟର: ପାସ୍କାଲର କାଲକୁଲେଟର ହେଉଛି ଏକ ଯାନ୍ତ୍ରିକ କାଲକୁଲେଟର ଯାହାକି 17 ଶତାବ୍ଦୀର ମଧ୍ୟଭାଗରେ ବ୍ଲେଜ୍ ପାସ୍କାଲଙ୍କ ଦ୍ୱାରା ଉଦ୍ଭାବିତ ହୋଇଥିଲା | ରୁଆନରେ ଟ୍ୟାକ୍ସର ସୁପରଭାଇଜର ଭାବରେ ତାଙ୍କ ପିତାଙ୍କ କାର୍ଯ୍ୟ ଆବଶ୍ୟକ କରୁଥିବା ପରିଶ୍ରମୀ ଗଣିତ ଗଣନା ଦ୍ୱାରା ପାସ୍କାଲ୍ ଏକ କାଲକୁଲେଟର ବିକାଶ କରିବାକୁ ନେତୃତ୍ୱ ନେଇଥିଲେ | ସିଧାସଳଖ ଦୁଇଟି ସଂଖ୍ୟା ଯୋଡିବା ଏବଂ ବାହାର କରିବା ଏବଂ ବାରମ୍ବାର ଯୋଗ କିମ୍ବା ବିତରଣ ମାଧ୍ୟମରେ ଗୁଣନ ଏବଂ ବିଭାଜନ କରିବା ପାଇଁ ସେ ମେସିନ୍ ଡିଜାଇନ୍ କରିଥିଲେ |
ଗାଣିତିକ ଅର୍ଥ: ଗଣିତ ଏବଂ ପରିସଂଖ୍ୟାନରେ, ଗାଣିତିକ ଅର୍ଥ , କିମ୍ବା କେବଳ ଅର୍ଥ ବା ହାରାହାରି , ସଂଗ୍ରହରେ ସଂଖ୍ୟା ଗଣନା ଦ୍ୱାରା ବିଭକ୍ତ ସଂଖ୍ୟା ସଂଗ୍ରହର ସମଷ୍ଟି ଅଟେ | ସଂଗ୍ରହ ପ୍ରାୟତ an ଏକ ପରୀକ୍ଷଣ କିମ୍ବା ପର୍ଯ୍ୟବେକ୍ଷଣଶୀଳ ଅଧ୍ୟୟନର ଫଳାଫଳର ଏକ ସେଟ୍, କିମ୍ବା ବାରମ୍ବାର ଏକ ସର୍ବେକ୍ଷଣରୁ ଫଳାଫଳର ଏକ ସେଟ୍ | ଗଣିତ ଏବଂ ପରିସଂଖ୍ୟାନରେ କେତେକ ପ୍ରସଙ୍ଗରେ "ଗାଣିତିକ ଅର୍ଥ" ଶବ୍ଦକୁ ଅଧିକ ପସନ୍ଦ କରାଯାଏ, କାରଣ ଏହା ଏହାକୁ ଅନ୍ୟ ଉପାୟଠାରୁ ଭିନ୍ନ କରିବାରେ ସାହାଯ୍ୟ କରିଥାଏ, ଯେପରିକି ଜ୍ୟାମିତିକ ଅର୍ଥ ଏବଂ ହାରମୋନିକ୍ ଅର୍ଥ |
ଗାଣିତିକ ଏବଂ ଜ୍ୟାମିତିକ ଅର୍ଥର ଅସମାନତା: ଗଣିତରେ, ଗାଣିତିକ ଏବଂ ଜ୍ୟାମିତିକ ଅର୍ଥର ଅସମାନତା , କିମ୍ବା ଅଧିକ ସଂକ୍ଷେପରେ AM - GM ଅସମାନତା ଦର୍ଶାଏ ଯେ ଅଣ-ନକାରାତ୍ମକ ପ୍ରକୃତ ସଂଖ୍ୟାର ତାଲିକାର ଗାଣିତିକ ଅର୍ଥ ସମାନ ତାଲିକାର ଜ୍ୟାମିତିକ ଅର୍ଥଠାରୁ ଅଧିକ କିମ୍ବା ସମାନ; ଏବଂ ଆହୁରି ମଧ୍ୟ, ଯଦି ତାଲିକାର ପ୍ରତ୍ୟେକ ସଂଖ୍ୟା ସମାନ ତେବେ ଦୁଇଟି ଅର୍ଥ ସମାନ |
ସାଧାରଣ (ଗଣିତ): ଗଣିତରେ, ଏକ ଆଦର୍ଶ ହେଉଛି ଏକ ବାସ୍ତବ କିମ୍ବା ଜଟିଳ ଭେକ୍ଟର ସ୍ପେସ୍ ଠାରୁ ଅଣ-ନେଗେଟିଭ୍ ରିଅଲ୍ ନମ୍ବର ପର୍ଯ୍ୟନ୍ତ ଏକ କାର୍ଯ୍ୟ ଯାହା ମୂଳରୁ ଦୂରତା ପରି କିଛି ଉପାୟରେ ଆଚରଣ କରେ: ଏହା ମାପିବା ସହିତ ଗତି କରେ, ତ୍ରିରଙ୍ଗା ଅସମାନତାର ଏକ ରୂପ ପାଳନ କରେ ଏବଂ କେବଳ ଶୂନ୍ୟ ଉତ୍ପତ୍ତି ବିଶେଷ ଭାବରେ, ମୂଳରୁ ଏକ ଭେକ୍ଟରର ଇଉକ୍ଲିଡିଆନ୍ ଦୂରତା ଏକ ଆଦର୍ଶ, ଯାହାକୁ ଇଉକ୍ଲିଡିଆନ୍ ନର୍ମା ବା 2-ନର୍ମା କୁହାଯାଏ, ଯାହା ନିଜେ ଏକ ଭେକ୍ଟରର ଆଭ୍ୟନ୍ତରୀଣ ଉତ୍ପାଦର ବର୍ଗ ମୂଳ ଭାବରେ ମଧ୍ୟ ବ୍ୟାଖ୍ୟା କରାଯାଇପାରେ |
ଗାଣିତିକ ସଂଖ୍ୟା: ସଂଖ୍ୟା ତତ୍ତ୍ In ରେ, ଏକ ଗାଣିତିକ ସଂଖ୍ୟା ହେଉଛି ଏକ ପୂର୍ଣ୍ଣ ସଂଖ୍ୟା ଯାହା ପାଇଁ ଏହାର ସକରାତ୍ମକ ବିଭାଜନର ହାରାହାରି ମଧ୍ୟ ଏକ ପୂର୍ଣ୍ଣ ସଂଖ୍ୟା | ଉଦାହରଣ ସ୍ .ରୁପ, 6 ହେଉଛି ଏକ ଗଣିତ ସଂଖ୍ୟା କାରଣ ଏହାର ବିଭାଜକଙ୍କ ହାରାହାରି |
ଏକ ହତ୍ୟାକାଣ୍ଡର ଗାଣିତିକ: ଆରିଥମେଟିକ୍ ଅଫ୍ ମର୍ଡର୍ ହେଉଛି 1991 ସୋଭିଏତ୍ କ୍ରାଇମ୍ ଫିଲ୍ମ, ଡିମିଟ୍ରି ସ୍ vet ଟୋଜାରୋଭଙ୍କ ନିର୍ଦ୍ଦେଶିତ |
ଆବେଲିଆନ୍ କିସମର ଗାଣିତିକ: ଗଣିତରେ, ଆବେଲିଆନ୍ କିସମର ଗାଣିତିକ ହେଉଛି ଏକ ଆବେଲିଆନ୍ କିସମର ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତର ଅଧ୍ୟୟନ, କିମ୍ବା ଆବେଲିଆନ୍ କିସମର ଏକ ପରିବାର | ଏହା ପିଆର ଡି ଫର୍ମାଟଙ୍କ ଅଧ୍ୟୟନକୁ ଫେରିଯାଏ ଯାହା ବର୍ତ୍ତମାନ ଏଲିପଟିକ୍ ବକ୍ର ଭାବରେ ସ୍ୱୀକୃତିପ୍ରାପ୍ତ; ଉଭୟ ଫଳାଫଳ ଏବଂ ଧାରଣା ଦୃଷ୍ଟିରୁ ଗାଣିତିକ ଜ୍ୟାମିତିର ଏକ ମହତ୍ area ପୂର୍ଣ୍ଣ କ୍ଷେତ୍ର ହୋଇପାରିଛି | ଏଥିମଧ୍ୟରୁ ଅଧିକାଂଶ ଏକ ଆବେଲିଆନ୍ ବିବିଧତା A ପାଇଁ ଏକ ସଂଖ୍ୟା କ୍ଷେତ୍ର K ଉପରେ ପୋଜ୍ ହୋଇପାରେ | କିମ୍ବା ସାଧାରଣତ। ଅଧିକ |
ଆବେଲିଆନ୍ କିସମର ଗାଣିତିକ: ଗଣିତରେ, ଆବେଲିଆନ୍ କିସମର ଗାଣିତିକ ହେଉଛି ଏକ ଆବେଲିଆନ୍ କିସମର ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତର ଅଧ୍ୟୟନ, କିମ୍ବା ଆବେଲିଆନ୍ କିସମର ଏକ ପରିବାର | ଏହା ପିଆର ଡି ଫର୍ମାଟଙ୍କ ଅଧ୍ୟୟନକୁ ଫେରିଯାଏ ଯାହା ବର୍ତ୍ତମାନ ଏଲିପଟିକ୍ ବକ୍ର ଭାବରେ ସ୍ୱୀକୃତିପ୍ରାପ୍ତ; ଉଭୟ ଫଳାଫଳ ଏବଂ ଧାରଣା ଦୃଷ୍ଟିରୁ ଗାଣିତିକ ଜ୍ୟାମିତିର ଏକ ମହତ୍ area ପୂର୍ଣ୍ଣ କ୍ଷେତ୍ର ହୋଇପାରିଛି | ଏଥିମଧ୍ୟରୁ ଅଧିକାଂଶ ଏକ ଆବେଲିଆନ୍ ବିବିଧତା A ପାଇଁ ଏକ ସଂଖ୍ୟା କ୍ଷେତ୍ର K ଉପରେ ପୋଜ୍ ହୋଇପାରେ | କିମ୍ବା ସାଧାରଣତ। ଅଧିକ |
ଆବେଲିଆନ୍ କିସମର ଗାଣିତିକ: ଗଣିତରେ, ଆବେଲିଆନ୍ କିସମର ଗାଣିତିକ ହେଉଛି ଏକ ଆବେଲିଆନ୍ କିସମର ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତର ଅଧ୍ୟୟନ, କିମ୍ବା ଆବେଲିଆନ୍ କିସମର ଏକ ପରିବାର | ଏହା ପିଆର ଡି ଫର୍ମାଟଙ୍କ ଅଧ୍ୟୟନକୁ ଫେରିଯାଏ ଯାହା ବର୍ତ୍ତମାନ ଏଲିପଟିକ୍ ବକ୍ର ଭାବରେ ସ୍ୱୀକୃତିପ୍ରାପ୍ତ; ଉଭୟ ଫଳାଫଳ ଏବଂ ଧାରଣା ଦୃଷ୍ଟିରୁ ଗାଣିତିକ ଜ୍ୟାମିତିର ଏକ ମହତ୍ area ପୂର୍ଣ୍ଣ କ୍ଷେତ୍ର ହୋଇପାରିଛି | ଏଥିମଧ୍ୟରୁ ଅଧିକାଂଶ ଏକ ଆବେଲିଆନ୍ ବିବିଧତା A ପାଇଁ ଏକ ସଂଖ୍ୟା କ୍ଷେତ୍ର K ଉପରେ ପୋଜ୍ ହୋଇପାରେ | କିମ୍ବା ସାଧାରଣତ। ଅଧିକ |
ସୀମିତ କ୍ଷେତ୍ର ଗଣିତ: ଗଣିତରେ, ସୀମିତ କ୍ଷେତ୍ର ଆରିଥମେଟିକ୍ ଏକ ସୀମିତ କ୍ଷେତ୍ରରେ ଗାଣିତିକ ଅଟେ ଯାହା ଯୁକ୍ତିଯୁକ୍ତ ସଂଖ୍ୟା କ୍ଷେତ୍ର ପରି ଏକ ଅସୀମ ସଂଖ୍ୟକ ଉପାଦାନ ସହିତ ଏକ କ୍ଷେତ୍ରରେ ଗଣିତର ବିପରୀତ ଅଟେ |
ସାଧାରଣ ଗାଣିତିକ: ସେଟ୍ ସିଦ୍ଧାନ୍ତର ଗାଣିତିକ କ୍ଷେତ୍ରରେ, ଅର୍ଡିନାଲ୍ ଆରିଥମେଟିକ୍ କ୍ରମାଗତ ସଂଖ୍ୟା ଉପରେ ତିନୋଟି ସାଧାରଣ କାର୍ଯ୍ୟକୁ ବର୍ଣ୍ଣନା କରେ: ଯୋଗ, ଗୁଣନ, ଏବଂ ଏକ୍ସପୋନ୍ସନ୍ | ପ୍ରତ୍ୟେକକୁ ମୁଖ୍ୟତ two ଦୁଇଟି ଭିନ୍ନ ଉପାୟରେ ବ୍ୟାଖ୍ୟା କରାଯାଇପାରେ: ଏକ ସ୍ପଷ୍ଟ ସୁସଜ୍ଜିତ ସେଟ୍ ନିର୍ମାଣ କରି ଯାହା ଅପରେସନ୍ କୁ ପ୍ରତିନିଧିତ୍ୱ କରେ କିମ୍ବା ଟ୍ରାନ୍ସଫାଇଟ୍ ରିସର୍ସନ୍ ବ୍ୟବହାର କରି | କ୍ୟାଣ୍ଟର ସାଧାରଣ ଫର୍ମ ଅର୍ଡିନାଲ୍ ଲେଖିବାର ଏକ ମାନକ ଉପାୟ ପ୍ରଦାନ କରେ | ଏହି ସାଧାରଣ ଅର୍ଡିନାଲ୍ ଅପରେସନ୍ ସହିତ, ଅର୍ଡିନାଲ୍ ଏବଂ ନିମ୍ବର ଅପରେସନ୍ ର "ପ୍ରାକୃତିକ" ଗାଣିତିକ ମଧ୍ୟ ଅଛି |
ଗାଣିତିକ: ଆରିଥମେଟିକ୍ ହେଉଛି ଗଣିତର ଏକ ଶାଖା ଯାହା ସଂଖ୍ୟାଗୁଡ଼ିକର ଅଧ୍ୟୟନକୁ ନେଇ ଗଠିତ, ବିଶେଷତ them ସେମାନଙ୍କ ଉପରେ ପାରମ୍ପାରିକ କାର୍ଯ୍ୟର ଗୁଣ - ଯୋଗ, ବିତରଣ, ଗୁଣନ, ବିଭାଜନ, ମୂଳ ଏବଂ ନିର୍ବାହ | ଆରିଥମେଟିକ୍ ହେଉଛି ସଂଖ୍ୟା ତତ୍ତ୍ an ର ଏକ ପ୍ରାଥମିକ ଅଂଶ, ଏବଂ ସଂଖ୍ୟା ଥିଓରୀକୁ ଆଧୁନିକ ଗଣିତର ଏକ ଉଚ୍ଚ ସ୍ତରୀୟ ବିଭାଗ ଭାବରେ ବିବେଚନା କରାଯାଏ, ବୀଜ୍, ଜ୍ୟାମିତି ଏବଂ ବିଶ୍ଳେଷଣ ସହିତ | ଆରିଥମେଟିକ୍ ଏବଂ ଉଚ୍ଚ ଆରିଥମେଟିକ୍ ଶବ୍ଦଗୁଡିକ ବିଂଶ ଶତାବ୍ଦୀର ଆରମ୍ଭ ପର୍ଯ୍ୟନ୍ତ ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତର ସମକକ୍ଷ ଭାବରେ ବ୍ୟବହୃତ ହୋଇଥିଲା ଏବଂ ବେଳେବେଳେ ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତର ଏକ ବ୍ୟାପକ ଅଂଶକୁ ସୂଚାଇବା ପାଇଁ ବ୍ୟବହୃତ ହୁଏ |
ଗାଣିତିକ: ଆରିଥମେଟିକ୍ ହେଉଛି ଗଣିତର ଏକ ଶାଖା ଯାହା ସଂଖ୍ୟାଗୁଡ଼ିକର ଅଧ୍ୟୟନକୁ ନେଇ ଗଠିତ, ବିଶେଷତ them ସେମାନଙ୍କ ଉପରେ ପାରମ୍ପାରିକ କାର୍ଯ୍ୟର ଗୁଣ - ଯୋଗ, ବିତରଣ, ଗୁଣନ, ବିଭାଜନ, ମୂଳ ଏବଂ ନିର୍ବାହ | ଆରିଥମେଟିକ୍ ହେଉଛି ସଂଖ୍ୟା ତତ୍ତ୍ an ର ଏକ ପ୍ରାଥମିକ ଅଂଶ, ଏବଂ ସଂଖ୍ୟା ଥିଓରୀକୁ ଆଧୁନିକ ଗଣିତର ଏକ ଉଚ୍ଚ ସ୍ତରୀୟ ବିଭାଗ ଭାବରେ ବିବେଚନା କରାଯାଏ, ବୀଜ୍, ଜ୍ୟାମିତି ଏବଂ ବିଶ୍ଳେଷଣ ସହିତ | ଆରିଥମେଟିକ୍ ଏବଂ ଉଚ୍ଚ ଆରିଥମେଟିକ୍ ଶବ୍ଦଗୁଡିକ ବିଂଶ ଶତାବ୍ଦୀର ଆରମ୍ଭ ପର୍ଯ୍ୟନ୍ତ ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତର ସମକକ୍ଷ ଭାବରେ ବ୍ୟବହୃତ ହୋଇଥିଲା ଏବଂ ବେଳେବେଳେ ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତର ଏକ ବ୍ୟାପକ ଅଂଶକୁ ସୂଚାଇବା ପାଇଁ ବ୍ୟବହୃତ ହୁଏ |
ଗାଣିତିକ: ଆରିଥମେଟିକ୍ ହେଉଛି ଗଣିତର ଏକ ଶାଖା ଯାହା ସଂଖ୍ୟାଗୁଡ଼ିକର ଅଧ୍ୟୟନକୁ ନେଇ ଗଠିତ, ବିଶେଷତ them ସେମାନଙ୍କ ଉପରେ ପାରମ୍ପାରିକ କାର୍ଯ୍ୟର ଗୁଣ - ଯୋଗ, ବିତରଣ, ଗୁଣନ, ବିଭାଜନ, ମୂଳ ଏବଂ ନିର୍ବାହ | ଆରିଥମେଟିକ୍ ହେଉଛି ସଂଖ୍ୟା ତତ୍ତ୍ an ର ଏକ ପ୍ରାଥମିକ ଅଂଶ, ଏବଂ ସଂଖ୍ୟା ଥିଓରୀକୁ ଆଧୁନିକ ଗଣିତର ଏକ ଉଚ୍ଚ ସ୍ତରୀୟ ବିଭାଗ ଭାବରେ ବିବେଚନା କରାଯାଏ, ବୀଜ୍, ଜ୍ୟାମିତି ଏବଂ ବିଶ୍ଳେଷଣ ସହିତ | ଆରିଥମେଟିକ୍ ଏବଂ ଉଚ୍ଚ ଆରିଥମେଟିକ୍ ଶବ୍ଦଗୁଡିକ ବିଂଶ ଶତାବ୍ଦୀର ଆରମ୍ଭ ପର୍ଯ୍ୟନ୍ତ ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତର ସମକକ୍ଷ ଭାବରେ ବ୍ୟବହୃତ ହୋଇଥିଲା ଏବଂ ବେଳେବେଳେ ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତର ଏକ ବ୍ୟାପକ ଅଂଶକୁ ସୂଚାଇବା ପାଇଁ ବ୍ୟବହୃତ ହୁଏ |
ଗାଣିତିକ: ଆରିଥମେଟିକ୍ ହେଉଛି ଗଣିତର ଏକ ଶାଖା ଯାହା ସଂଖ୍ୟାଗୁଡ଼ିକର ଅଧ୍ୟୟନକୁ ନେଇ ଗଠିତ, ବିଶେଷତ them ସେମାନଙ୍କ ଉପରେ ପାରମ୍ପାରିକ କାର୍ଯ୍ୟର ଗୁଣ - ଯୋଗ, ବିତରଣ, ଗୁଣନ, ବିଭାଜନ, ମୂଳ ଏବଂ ନିର୍ବାହ | ଆରିଥମେଟିକ୍ ହେଉଛି ସଂଖ୍ୟା ତତ୍ତ୍ an ର ଏକ ପ୍ରାଥମିକ ଅଂଶ, ଏବଂ ସଂଖ୍ୟା ଥିଓରୀକୁ ଆଧୁନିକ ଗଣିତର ଏକ ଉଚ୍ଚ ସ୍ତରୀୟ ବିଭାଗ ଭାବରେ ବିବେଚନା କରାଯାଏ, ବୀଜ୍, ଜ୍ୟାମିତି ଏବଂ ବିଶ୍ଳେଷଣ ସହିତ | ଆରିଥମେଟିକ୍ ଏବଂ ଉଚ୍ଚ ଆରିଥମେଟିକ୍ ଶବ୍ଦଗୁଡିକ ବିଂଶ ଶତାବ୍ଦୀର ଆରମ୍ଭ ପର୍ଯ୍ୟନ୍ତ ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତର ସମକକ୍ଷ ଭାବରେ ବ୍ୟବହୃତ ହୋଇଥିଲା ଏବଂ ବେଳେବେଳେ ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତର ଏକ ବ୍ୟାପକ ଅଂଶକୁ ସୂଚାଇବା ପାଇଁ ବ୍ୟବହୃତ ହୁଏ |
ପୂର୍ଣ୍ଣ ଓଭରଫ୍ଲୋ: କମ୍ପ୍ୟୁଟର ପ୍ରୋଗ୍ରାମିଂରେ, ଏକ ଇଣ୍ଟିଜର୍ ଓଭରଫ୍ଲୋ ହୁଏ ଯେତେବେଳେ ଏକ ଆରିଥମେଟିକ୍ ଅପରେସନ୍ ଏକ ସାଂଖ୍ୟିକ ମୂଲ୍ୟ ସୃଷ୍ଟି କରିବାକୁ ଚେଷ୍ଟା କରେ ଯାହା ପରିସର ବାହାରେ ଯାହା ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ସଂଖ୍ୟା ସହିତ ଉପସ୍ଥାପିତ ହୋଇପାରେ - ସର୍ବାଧିକ କିମ୍ବା ସର୍ବନିମ୍ନ ପ୍ରତିନିଧିତ୍ value ମୂଲ୍ୟଠାରୁ କମ୍ |
P-adic L- କାର୍ଯ୍ୟ: ଗଣିତରେ, ଏକ p- ଆଡିକ୍ ଜେଟା ଫଙ୍କସନ୍ , କିମ୍ବା ସାଧାରଣତ a p -adic L- ଫଙ୍କସନ୍ , ରିମାନ୍ ଜେଟା ଫଙ୍କସନ୍, କିମ୍ବା ଅଧିକ ସାଧାରଣ L- ଫଙ୍କସନ୍ ସହିତ ସମାନ କାର୍ଯ୍ୟ, କିନ୍ତୁ ଯାହାର ଡୋମେନ୍ ଏବଂ ଟାର୍ଗେଟ୍ p-adic | ଉଦାହରଣ ସ୍ୱରୂପ, ଡୋମେନ୍ p -adic ଗଣନ Z p, ଏକ profinite p -group, କିମ୍ବା ଗାଲୋଇସ ଉପସ୍ଥାପନା ଏକ p -adic ପରିବାର ହେବ ନାହିଁ, ଏବଂ ପ୍ରତିଛବି p -adic ସଂଖ୍ୟା Q p କିମ୍ବା ଏହାର algebraic ନିବଦ୍ଧ ହେବ ନାହିଁ।
ଗୁରୁତ୍ୱପୂର୍ଣ୍ଣ ସଂଖ୍ୟା: ପୋଜିସନାଲ୍ ନୋଟେସନ୍ ରେ ଏକ ସଂଖ୍ୟାର ମହତ୍ figures ପୂର୍ଣ ସଂଖ୍ୟା ହେଉଛି ସଂଖ୍ୟାରେ ଥିବା ସଂଖ୍ୟା ଯାହା ନିର୍ଭରଯୋଗ୍ୟ ଏବଂ କିଛି ପରିମାଣ ସୂଚାଇବା ପାଇଁ ସମ୍ପୂର୍ଣ୍ଣ ଆବଶ୍ୟକ | ଯଦି କିଛି ପରିମାପର ଫଳାଫଳକୁ ପ୍ରକାଶ କରୁଥିବା ସଂଖ୍ୟାରେ ମାପ ରିଜୋଲ୍ୟୁସନ୍ ଦ୍ୱାରା ଅନୁମୋଦିତ ଅଙ୍କ ଅପେକ୍ଷା ଅଧିକ ସଂଖ୍ୟା ଥାଏ, କେବଳ ମାପ ରିଜୋଲ୍ୟୁସନ୍ ଦ୍ୱାରା ଅନୁମତି ପ୍ରାପ୍ତ ସଂଖ୍ୟାଗୁଡ଼ିକ ନିର୍ଭରଯୋଗ୍ୟ ତେଣୁ କେବଳ ଏଗୁଡ଼ିକ ଗୁରୁତ୍ୱପୂର୍ଣ୍ଣ ସଂଖ୍ୟା ହୋଇପାରେ | ଉଦାହରଣ ସ୍ୱରୂପ, ଯଦି ଏକ ଲମ୍ବ ମାପ 114.8 ମିମି ଦେଇଥାଏ ଯେତେବେଳେ ମାପରେ ବ୍ୟବହୃତ ଶାସକ ଉପରେ ଚିହ୍ନ ମଧ୍ୟରେ କ୍ଷୁଦ୍ରତମ ବ୍ୟବଧାନ 1 ମିମି, ତେବେ ପ୍ରଥମ ତିନୋଟି ଅଙ୍କ କେବଳ ବିଶ୍ୱାସଯୋଗ୍ୟ ତେଣୁ ଗୁରୁତ୍ୱପୂର୍ଣ୍ଣ ସଂଖ୍ୟା ହୋଇପାରେ | ଏହି ସଂଖ୍ୟାଗୁଡିକ ମଧ୍ୟରେ, ଶେଷ ଅଙ୍କରେ ଅନିଶ୍ଚିତତା ଅଛି କିନ୍ତୁ ଏହା ଏକ ଗୁରୁତ୍ୱପୂର୍ଣ୍ଣ ବ୍ୟକ୍ତିତ୍ୱ ଭାବରେ ବିବେଚନା କରାଯାଏ କାରଣ ଅଙ୍କଗୁଡିକ ଅନିଶ୍ଚିତ କିନ୍ତୁ ନିର୍ଭରଯୋଗ୍ୟ ଗୁରୁତ୍ୱପୂର୍ଣ୍ଣ ସଂଖ୍ୟା ଭାବରେ ବିବେଚନା କରାଯାଏ | ଅନ୍ୟ ଏକ ଉଦାହରଣ ହେଉଛି ± 0.05 L ର ଅନିଶ୍ଚିତତା ସହିତ 2.98 L ର ଭଲ୍ୟୁମ୍ ମାପ | ପ୍ରକୃତ ଭଲ୍ୟୁମ୍ କ ewhere ଣସି ସ୍ଥାନରେ 2.93 L ରୁ 3.03 L ମଧ୍ୟରେ ଅଛି ଯଦିଓ ସମସ୍ତ ତିନୋଟି ସଂଖ୍ୟା ନିଶ୍ଚିତ ନୁହେଁ କିନ୍ତୁ ନିର୍ଭରଯୋଗ୍ୟ କାରଣ ଏହା ଗ୍ରହଣୀୟ ଅନିଶ୍ଚିତତା ସହିତ ପ୍ରକୃତ ଭଲ୍ୟୁମକୁ ସୂଚିତ କରେ | । ତେଣୁ, ଏଗୁଡ଼ିକ ହେଉଛି ଗୁରୁତ୍ୱପୂର୍ଣ୍ଣ ସଂଖ୍ୟା |
ଗାଣିତିକ ପ୍ରଗତି: ଏକ ଆରିଥମେଟିକ୍ ପ୍ରଗତି (AP) ବା ଗାଣିତିକ କ୍ରମ ହେଉଛି ସଂଖ୍ୟାଗୁଡ଼ିକର କ୍ରମ ଯେପରି କ୍ରମାଗତ ଶବ୍ଦଗୁଡ଼ିକ ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ ସ୍ଥିର ଅଟେ | ଉଦାହରଣ ସ୍ୱରୂପ, କ୍ରମ 5, 7, 9, 11, 13, 15 ,। 2 ର ସାଧାରଣ ପାର୍ଥକ୍ୟ ସହିତ ଏକ ଗାଣିତିକ ପ୍ରଗତି |
ଗାଣିତିକ ପ୍ରଗତି ଖେଳ: ଗାଣିତିକ ପ୍ରଗତି ଖେଳ ହେଉଛି ଏକ ପୋଜିସନାଲ୍ ଖେଳ ଯେଉଁଠାରେ ଦୁଇ ଖେଳାଳି ବିକଳ୍ପ ଭାବରେ ସଂଖ୍ୟା ବାଛନ୍ତି, ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଆକାରର ସମ୍ପୂର୍ଣ୍ଣ ଗାଣିତିକ ପ୍ରଗତି ଦଖଲ କରିବାକୁ ଚେଷ୍ଟା କରନ୍ତି |
ଗାଣିତିକ ପ୍ରଗତି: ଏକ ଆରିଥମେଟିକ୍ ପ୍ରଗତି (AP) ବା ଗାଣିତିକ କ୍ରମ ହେଉଛି ସଂଖ୍ୟାଗୁଡ଼ିକର କ୍ରମ ଯେପରି କ୍ରମାଗତ ଶବ୍ଦଗୁଡ଼ିକ ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ ସ୍ଥିର ଅଟେ | ଉଦାହରଣ ସ୍ୱରୂପ, କ୍ରମ 5, 7, 9, 11, 13, 15 ,। 2 ର ସାଧାରଣ ପାର୍ଥକ୍ୟ ସହିତ ଏକ ଗାଣିତିକ ପ୍ରଗତି |
ରିଙ୍ଗ (ଗଣିତ): ଗଣିତରେ, ରିଙ୍ଗଗୁଡ଼ିକ ହେଉଛି ବୀଜ ବର୍ଣ୍ଣିତ ସଂରଚନା ଯାହା କ୍ଷେତ୍ରଗୁଡ଼ିକୁ ସାଧାରଣ କରିଥାଏ: ଗୁଣନ କ୍ରମାଗତ ହେବା ଆବଶ୍ୟକ ନୁହେଁ ଏବଂ ଗୁଣନ ଇନଭର୍ସ ରହିବା ଆବଶ୍ୟକ ନାହିଁ | ଅନ୍ୟ ଅର୍ଥରେ, ଗୋଟିଏ ରିଙ୍ଗ ହେଉଛି ଦୁଇଟି ବାଇନାରୀ ଅପରେସନ୍ ସହିତ ସଜ୍ଜିତ ଗୁଣ ଯାହା ଇଣ୍ଟିଜର୍ସର ଯୋଗ ଏବଂ ଗୁଣନ ସହିତ ସମାନ ଅଟେ | ରିଙ୍ଗ୍ ଉପାଦାନଗୁଡିକ ସଂଖ୍ୟା ହୋଇପାରେ ଯେପରିକି ଇଣ୍ଟିଜର୍ କିମ୍ବା ଜଟିଳ ସଂଖ୍ୟା, କିନ୍ତୁ ସେଗୁଡ଼ିକ ଅଣ-ସାଂଖ୍ୟିକ ବସ୍ତୁ ହୋଇପାରେ ଯେପରିକି ପଲିନୋମିଆଲ୍, ବର୍ଗ ମ୍ୟାଟ୍ରିକ୍ସ, ଫଙ୍କସନ୍, ଏବଂ ପାୱାର୍ ସିରିଜ୍ |
ଗାଣିତିକ କ୍ରମ: ଗାଣିତିକ ତର୍କ ରେ, arithmetical ଅନୁକ୍ରମ, ଗାଣିତିକ ଅନୁକ୍ରମ କିମ୍ବା Kleene-Mostowski ଅନୁକ୍ରମ ସେମାନଙ୍କୁ ବ୍ୟାଖ୍ୟା ଯେ ସୂତ୍ର ଜଟିଳତାକୁ ଉପରେ ଆଧାରିତ ନିର୍ଦ୍ଦିଷ୍ଟ େସଟଗୁଡ଼ିକ classifies। ଯେକ Any ଣସି ସେଟ୍ ଯାହା ଏକ ଶ୍ରେଣୀକରଣ ଗ୍ରହଣ କରେ ଏହାକୁ ଗଣିତ କୁହାଯାଏ |
ଫେରସ୍ତ ହାର: ଆର୍ଥିକ କ୍ଷେତ୍ରରେ, ରିଟର୍ଣ୍ଣ ହେଉଛି ଏକ ବିନିଯୋଗ ଉପରେ ଲାଭ | ଏଥିରେ ପୁଞ୍ଜି ବିନିଯୋଗର ମୂଲ୍ୟରେ ଯେକ change ଣସି ପରିବର୍ତ୍ତନ, ଏବଂ / କିମ୍ବା ନଗଦ ପ୍ରବାହ ରହିଥାଏ ଯାହା ନିବେଶକ ସେହି ନିବେଶରୁ ଗ୍ରହଣ କରନ୍ତି, ଯେପରିକି ସୁଧ ଦେୟ, କୁପନ୍, ନଗଦ ଡିଭିଡେଣ୍ଡ୍, ଷ୍ଟକ୍ ଡିଭିଡେଣ୍ଡ୍ କିମ୍ବା ଏକ ଉତ୍ପାଦିତ କିମ୍ବା ସଂରକ୍ଷିତ ଉତ୍ପାଦରୁ ପେ ଅଫ୍ | ଏହା ସଂପୂର୍ଣ୍ଣ ଶବ୍ଦରେ କିମ୍ବା ବିନିଯୋଗ ହୋଇଥିବା ପରିମାଣର ଶତକଡ଼ା ପରି ମାପ କରାଯାଇପାରେ | ଶେଷକୁ ହୋଲ୍ଡିଂ ପିରିୟଡ୍ ରିଟର୍ନ ମଧ୍ୟ କୁହାଯାଏ |
ଗାଣିତିକ ପରିବର୍ତ୍ତନ: କମ୍ପ୍ୟୁଟର ପ୍ରୋଗ୍ରାମିଂରେ, ଏକ ଗାଣିତିକ ଶିଫ୍ଟ ହେଉଛି ଏକ ଶିଫ୍ଟ ଅପରେଟର, ବେଳେବେଳେ ଏକ ସ୍ signed ାକ୍ଷରିତ ଶିଫ୍ଟ କୁହାଯାଏ | ଦୁଇଟି ମ basic ଳିକ ପ୍ରକାର ହେଉଛି ଗାଣିତିକ ବାମ ଶିଫ୍ଟ ଏବଂ ଗାଣିତିକ ଡାହାଣ ଶିଫ୍ଟ | ବାଇନାରୀ ନମ୍ବର ପାଇଁ ଏହା ଏକ ଟିକେ ବୁଦ୍ଧ ଅପରେସନ୍ ଯାହା ଏହାର ଅପରେଣ୍ଡର ସମସ୍ତ ବିଟ୍ ସ୍ଥାନାନ୍ତର କରେ | ଅପରେଣ୍ଡରେ ଥିବା ପ୍ରତ୍ୟେକ ବିଟ୍ କେବଳ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ସଂଖ୍ୟକ ବିଟ୍ ପୋଜିସନ୍ ସ୍ଥାନାନ୍ତରିତ ହୁଏ, ଏବଂ ଖାଲି ବିଟ୍-ପୋଜିସନ୍ ଗୁଡିକ ପୂର୍ଣ୍ଣ ହୁଏ | ସମସ୍ତ 0s ରେ ଭରିବା ପରିବର୍ତ୍ତେ, ଲଜିକାଲ୍ ସିଫ୍ଟ ପରି, ଡାହାଣକୁ ଯିବାବେଳେ ବାମପଟ ବିଟ୍ ନକଲ ହୁଏ | ସମସ୍ତ ଖାଲି ପଦବୀ ପୂରଣ କରନ୍ତୁ |
ଗାଣିତିକ ରିଙ୍ଗ: ଏକ commutative ମୁଦି R arithmetical ବୋଲି କହିଲେ ହୋଇଥାଏ algebra ରେ, ନିମ୍ନଲିଖିତ ସମାନ ଅବସ୍ଥା ଯେକୌଣସି ଧାରଣ ଯଦି: ଲୋକାଲାଇଜେସନ୍ ର R ରେ ପ୍ରତ୍ୟେକ ସର୍ବାଧିକ ଆଦର୍ଶ ପାଇଁ ଏକ ୟୁନିସେରିଆଲ୍ ରିଙ୍ଗ | R ର ସମସ୍ତ ଆଦର୍ଶ ପାଇଁ | , ଏବଂ , ସମସ୍ତ ଆଦର୍ଶ ପାଇଁ | , ଏବଂ ,
ଗାଣିତିକ ଦଉଡି: ଗାଣିତିକ ଦଉଡି ବା ଗଣ୍ଠି ଦଉଡି ମଧ୍ୟଯୁଗରେ ବହୁଳ ଭାବରେ ବ୍ୟବହୃତ ଗଣିତ ଉପକରଣ ଥିଲା ଯାହା ଅନେକ ଗାଣିତିକ ଏବଂ ଜ୍ୟାମିତିକ ସମସ୍ୟାର ସମାଧାନ ପାଇଁ ବ୍ୟବହୃତ ହୋଇପାରେ |
ଆରାକେଲୋଭ୍ ସିଦ୍ଧାନ୍ତ: ଗଣିତରେ, ଆରାକେଲୋଭ୍ ସିଦ୍ଧାନ୍ତ ହେଉଛି ଡାଇଓଫାଣ୍ଟାଇନ୍ ଜ୍ୟାମିତିର ଏକ ଆଭିମୁଖ୍ୟ, ଯାହା ସୁରେନ୍ ଆରାକେଲୋଭ୍ ପାଇଁ ନାମିତ | ଉଚ୍ଚ ଆକାରରେ ଡାଇଓଫାଣ୍ଟାଇନ୍ ସମୀକରଣ ଅଧ୍ୟୟନ ପାଇଁ ଏହା ବ୍ୟବହୃତ ହୁଏ |
ବିସ୍ତୃତ ଆନାଲିଟିକ୍ ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତ: ଅବଷ୍ଟ୍ରାକ୍ଟ ଆନାଲିଟିକ୍ ନମ୍ବର ସିଦ୍ଧାନ୍ତ ହେଉଛି ଗଣିତର ଏକ ଶାଖା ଯାହା ଶାସ୍ତ୍ରୀୟ ଆନାଲିଟିକ୍ ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତର ଧାରଣା ଏବଂ କ ques ଶଳକୁ ନେଇଥାଏ ଏବଂ ଏହାକୁ ବିଭିନ୍ନ ଗାଣିତିକ କ୍ଷେତ୍ରରେ ପ୍ରୟୋଗ କରିଥାଏ | ଶାସ୍ତ୍ରୀୟ ପ୍ରାଇମ୍ ନମ୍ବର ଥିଓରେମ୍ ଏକ ପ୍ରୋଟୋଟାଇପିକାଲ୍ ଉଦାହରଣ ଭାବରେ କାର୍ଯ୍ୟ କରେ, ଏବଂ ଅବଷ୍ଟ୍ରାକ୍ଟ ଅସ୍ମିପଟୋଟିକ୍ ବଣ୍ଟନ ଫଳାଫଳ ଉପରେ ଗୁରୁତ୍ୱ ଦିଆଯାଇଛି | ବିଂଶ ଶତାବ୍ଦୀରେ ଜନ୍ ନୋପଫମାଚର୍ ଏବଂ ଆର୍ନ ବେର୍ଲିଙ୍ଗଙ୍କ ପରି ଗଣିତଜ୍ଞଙ୍କ ଦ୍ The ାରା ଏହି ସିଦ୍ଧାନ୍ତ ଉଦ୍ଭାବନ କରାଯାଇଥିଲା ଏବଂ ବିକଶିତ ହୋଇଥିଲା |
ଗାଣିତିକ ପ୍ରଗତି: ଏକ ଆରିଥମେଟିକ୍ ପ୍ରଗତି (AP) ବା ଗାଣିତିକ କ୍ରମ ହେଉଛି ସଂଖ୍ୟାଗୁଡ଼ିକର କ୍ରମ ଯେପରି କ୍ରମାଗତ ଶବ୍ଦଗୁଡ଼ିକ ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ ସ୍ଥିର ଅଟେ | ଉଦାହରଣ ସ୍ୱରୂପ, କ୍ରମ 5, 7, 9, 11, 13, 15 ,। 2 ର ସାଧାରଣ ପାର୍ଥକ୍ୟ ସହିତ ଏକ ଗାଣିତିକ ପ୍ରଗତି |
ଗାଣିତିକ ପ୍ରଗତି: ଏକ ଆରିଥମେଟିକ୍ ପ୍ରଗତି (AP) ବା ଗାଣିତିକ କ୍ରମ ହେଉଛି ସଂଖ୍ୟାଗୁଡ଼ିକର କ୍ରମ ଯେପରି କ୍ରମାଗତ ଶବ୍ଦଗୁଡ଼ିକ ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ ସ୍ଥିର ଅଟେ | ଉଦାହରଣ ସ୍ୱରୂପ, କ୍ରମ 5, 7, 9, 11, 13, 15 ,। 2 ର ସାଧାରଣ ପାର୍ଥକ୍ୟ ସହିତ ଏକ ଗାଣିତିକ ପ୍ରଗତି |
ଗାଣିତିକ ସେଟ୍: ଗାଣିତିକ ତର୍କରେ, ଏକ ଗାଣିତିକ ସେଟ୍ ହେଉଛି ପ୍ରାକୃତିକ ସଂଖ୍ୟାଗୁଡ଼ିକର ଏକ ସେଟ୍ ଯାହା ପ୍ରଥମ କ୍ରମର ପିଆନୋ ଗାଣିତିକର ଏକ ସୂତ୍ର ଦ୍ୱାରା ବ୍ୟାଖ୍ୟା କରାଯାଇପାରେ | ଗାଣିତିକ ସେଟ୍ ଗୁଡିକ ଗାଣିତିକ କ୍ରମବଦ୍ଧତା ଦ୍ୱାରା ବର୍ଗୀକୃତ |
ଗାଣିତିକ ପରିବର୍ତ୍ତନ: କମ୍ପ୍ୟୁଟର ପ୍ରୋଗ୍ରାମିଂରେ, ଏକ ଗାଣିତିକ ଶିଫ୍ଟ ହେଉଛି ଏକ ଶିଫ୍ଟ ଅପରେଟର, ବେଳେବେଳେ ଏକ ସ୍ signed ାକ୍ଷରିତ ଶିଫ୍ଟ କୁହାଯାଏ | ଦୁଇଟି ମ basic ଳିକ ପ୍ରକାର ହେଉଛି ଗାଣିତିକ ବାମ ଶିଫ୍ଟ ଏବଂ ଗାଣିତିକ ଡାହାଣ ଶିଫ୍ଟ | ବାଇନାରୀ ନମ୍ବର ପାଇଁ ଏହା ଏକ ଟିକେ ବୁଦ୍ଧ ଅପରେସନ୍ ଯାହା ଏହାର ଅପରେଣ୍ଡର ସମସ୍ତ ବିଟ୍ ସ୍ଥାନାନ୍ତର କରେ | ଅପରେଣ୍ଡରେ ଥିବା ପ୍ରତ୍ୟେକ ବିଟ୍ କେବଳ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ସଂଖ୍ୟକ ବିଟ୍ ପୋଜିସନ୍ ସ୍ଥାନାନ୍ତରିତ ହୁଏ, ଏବଂ ଖାଲି ବିଟ୍-ପୋଜିସନ୍ ଗୁଡିକ ପୂର୍ଣ୍ଣ ହୁଏ | ସମସ୍ତ 0s ରେ ଭରିବା ପରିବର୍ତ୍ତେ, ଲଜିକାଲ୍ ସିଫ୍ଟ ପରି, ଡାହାଣକୁ ଯିବାବେଳେ ବାମପଟ ବିଟ୍ ନକଲ ହୁଏ | ସମସ୍ତ ଖାଲି ପଦବୀ ପୂରଣ କରନ୍ତୁ |
ମାନସିକ ଗଣନା: ମାନସିକ ଗଣନା କେବଳ ମାନବ ମସ୍ତିଷ୍କ ବ୍ୟବହାର କରି ଗାଣିତିକ ଗଣନାକୁ ନେଇ ଗଠିତ, କାଲକୁଲେଟର ପରି କ supplies ଣସି ଯୋଗାଣ କିମ୍ବା ଉପକରଣର କ help ଣସି ସାହାଯ୍ୟ ବିନା | ଯେତେବେଳେ ଗଣନା ଉପକରଣଗୁଡ଼ିକ ଉପଲବ୍ଧ ନଥାଏ, ଯେତେବେଳେ ଏହା ଅନ୍ୟ ଗଣନାର ମାଧ୍ୟମ ଅପେକ୍ଷା ତୀବ୍ର ହୁଏ, କିମ୍ବା ଏକ ପ୍ରତିଯୋଗିତାମୂଳକ ପ୍ରସଙ୍ଗରେ ମଧ୍ୟ ଲୋକମାନେ ମାନସିକ ଗଣନା ବ୍ୟବହାର କରନ୍ତି | ମାନସିକ ଗଣନା ପ୍ରାୟତ specific ନିର୍ଦ୍ଦିଷ୍ଟ ପ୍ରକାରର ସମସ୍ୟା ପାଇଁ ପ୍ରସ୍ତୁତ ନିର୍ଦ୍ଦିଷ୍ଟ କ ques ଶଳର ବ୍ୟବହାରକୁ ଅନ୍ତର୍ଭୁକ୍ତ କରିଥାଏ | ମାନସିକ ଗଣନା କରିବାକୁ ଅସାଧାରଣ ଉଚ୍ଚ କ୍ଷମତା ଥିବା ଲୋକଙ୍କୁ ମାନସିକ କାଲକୁଲେଟର ବା ବଜ୍ର କାଲକୁଲେଟର s କୁହାଯାଏ |
ମାନସିକ ଗଣନା: ମାନସିକ ଗଣନା କେବଳ ମାନବ ମସ୍ତିଷ୍କ ବ୍ୟବହାର କରି ଗାଣିତିକ ଗଣନାକୁ ନେଇ ଗଠିତ, କାଲକୁଲେଟର ପରି କ supplies ଣସି ଯୋଗାଣ କିମ୍ବା ଉପକରଣର କ help ଣସି ସାହାଯ୍ୟ ବିନା | ଯେତେବେଳେ ଗଣନା ଉପକରଣଗୁଡ଼ିକ ଉପଲବ୍ଧ ନଥାଏ, ଯେତେବେଳେ ଏହା ଅନ୍ୟ ଗଣନାର ମାଧ୍ୟମ ଅପେକ୍ଷା ତୀବ୍ର ହୁଏ, କିମ୍ବା ଏକ ପ୍ରତିଯୋଗିତାମୂଳକ ପ୍ରସଙ୍ଗରେ ମଧ୍ୟ ଲୋକମାନେ ମାନସିକ ଗଣନା ବ୍ୟବହାର କରନ୍ତି | ମାନସିକ ଗଣନା ପ୍ରାୟତ specific ନିର୍ଦ୍ଦିଷ୍ଟ ପ୍ରକାରର ସମସ୍ୟା ପାଇଁ ପ୍ରସ୍ତୁତ ନିର୍ଦ୍ଦିଷ୍ଟ କ ques ଶଳର ବ୍ୟବହାରକୁ ଅନ୍ତର୍ଭୁକ୍ତ କରିଥାଏ | ମାନସିକ ଗଣନା କରିବାକୁ ଅସାଧାରଣ ଉଚ୍ଚ କ୍ଷମତା ଥିବା ଲୋକଙ୍କୁ ମାନସିକ କାଲକୁଲେଟର ବା ବଜ୍ର କାଲକୁଲେଟର s କୁହାଯାଏ |
ସୁସ୍ଥତା: ତର୍କରେ, ଅଧିକ ସଠିକ୍ ଭାବରେ deductive ଯୁକ୍ତିରେ, ଯଦି ଉଭୟ ଫର୍ମରେ ବ valid ଧ ଏବଂ ଏହାର ପରିସର ସତ୍ୟ ତେବେ ଏକ ଯୁକ୍ତି ଶବ୍ଦ ଅଟେ | ଗାଣିତିକ ତର୍କରେ ସାଉଣ୍ଡେସନର ମଧ୍ୟ ଏକ ସମ୍ବନ୍ଧିତ ଅର୍ଥ ଅଛି, ଯେଉଁଠାରେ ଲଜିକାଲ୍ ସିଷ୍ଟମଗୁଡ଼ିକ ସଠିକ୍ ଏବଂ ଯଦି ସିଷ୍ଟମରେ ପ୍ରମାଣିତ ହୋଇପାରେ ପ୍ରତ୍ୟେକ ସୂତ୍ର ସିଷ୍ଟମର ସେମାଣ୍ଟିକ୍ସ ସହିତ ଯୁକ୍ତିଯୁକ୍ତ ଭାବରେ ବ valid ଧ ଅଟେ |
ଆର୍କିମିଡିଆନ୍ ସ୍ପିରାଲ୍: ଖ୍ରୀଷ୍ଟପୂର୍ବ 3rd ୟ ଶତାବ୍ଦୀର ଗ୍ରୀକ୍ ଗଣିତଜ୍ଞ ଆର୍କିମିଡିସ୍ଙ୍କ ନାମରେ ନାମିତ ଆର୍କିମିଡିଆନ୍ ସ୍ପିରାଲ୍ | ଏହା ଏକ ବିନ୍ଦୁ ସମୟ ସହିତ ଅବସ୍ଥାନ ସହିତ ଅନୁରୂପ ଅବସ୍ଥାନ ଅଟେ ଯାହାକି ଏକ ସ୍ଥିର ବିନ୍ଦୁରୁ ଏକ ଗତି ସହିତ ଏକ ସ୍ଥିର ଗତି ସହିତ ସ୍ଥିର କୋଣାର୍କ ବେଗ ସହିତ ଘୂର୍ଣ୍ଣନ କରେ | ସମାନ ଭାବରେ, ପୋଲାର କୋର୍ଡିନେଟ୍ସରେ ( r , θ ) ଏହାକୁ ସମୀକରଣ ଦ୍ୱାରା ବର୍ଣ୍ଣନା କରାଯାଇପାରେ |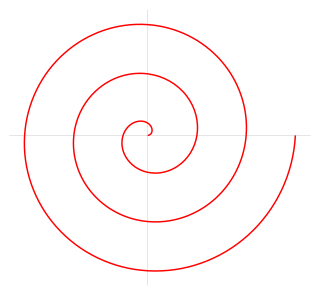
ଗାଣିତିକ ଗୋଷ୍ଠୀ: ଗଣିତରେ, ଏକ ଗାଣିତିକ ଗୋଷ୍ଠୀ ହେଉଛି ଏକ ଗୋଷ୍ଠୀ ଯାହାକି ଏକ ବୀଜ ବର୍ଣ୍ଣିତ ଗୋଷ୍ଠୀର ପୂର୍ଣ୍ଣ ପଏଣ୍ଟ ଭାବରେ ପ୍ରାପ୍ତ ହୋଇଛି | ଚତୁର୍ଥାଂଶ ଫର୍ମଗୁଡିକର ଗାଣିତିକ ଗୁଣ ଏବଂ ସଂଖ୍ୟା ତତ୍ତ୍ other ରେ ଅନ୍ୟାନ୍ୟ ଶାସ୍ତ୍ରୀୟ ବିଷୟଗୁଡିକ ଅଧ୍ୟୟନରେ ସେମାନେ ସ୍ natural ାଭାବିକ ଭାବରେ ଉଭା ହୁଅନ୍ତି | ସେମାନେ ରିମାନିଆନ୍ ମେନିଫୋଲ୍ଡର ଅତି ଆକର୍ଷଣୀୟ ଉଦାହରଣ ମଧ୍ୟ ସୃଷ୍ଟି କରନ୍ତି ଏବଂ ତେଣୁ ଭିନ୍ନ ଭିନ୍ନ ଜ୍ୟାମିତି ଏବଂ ଟପୋଲୋଜି ପ୍ରତି ଆଗ୍ରହର ବିଷୟ | ଶେଷରେ, ଏହି ଦୁଇଟି ବିଷୟ ଅଟୋମୋର୍ଫିକ୍ ଫର୍ମଗୁଡିକର ସିଦ୍ଧାନ୍ତରେ ଯୋଗଦାନ କରେ ଯାହା ଆଧୁନିକ ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତରେ ମ fundamental ଳିକ ଅଟେ |
ଗାଣିତିକ ପ୍ରଗତି: ଏକ ଆରିଥମେଟିକ୍ ପ୍ରଗତି (AP) ବା ଗାଣିତିକ କ୍ରମ ହେଉଛି ସଂଖ୍ୟାଗୁଡ଼ିକର କ୍ରମ ଯେପରି କ୍ରମାଗତ ଶବ୍ଦଗୁଡ଼ିକ ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ ସ୍ଥିର ଅଟେ | ଉଦାହରଣ ସ୍ୱରୂପ, କ୍ରମ 5, 7, 9, 11, 13, 15 ,। 2 ର ସାଧାରଣ ପାର୍ଥକ୍ୟ ସହିତ ଏକ ଗାଣିତିକ ପ୍ରଗତି |
ଗାଣିତିକ ପୃଷ୍ଠ: ଗଣିତରେ, ଭଗ୍ନାଂଶ କ୍ଷେତ୍ର ସହିତ ଏକ ଡେଡେକିଣ୍ଡ ଡୋମେନ୍ R ଉପରେ ଏକ ଗଣିତ ପୃଷ୍ଠ | ଏକ ଜ୍ୟାମିତିକ ବସ୍ତୁ ହେଉଛି ଗୋଟିଏ ପାରମ୍ପାରିକ ଡାଇମେନ୍ସନ୍, ଏବଂ ଅନ୍ୟ ଏକ ଡାଇମେନ୍ସନ୍ ପ୍ରାଇମ୍ସର ଅସୀମତା ଦ୍ୱାରା ପ୍ରଦତ୍ତ | ଯେତେବେଳେ R ହେଉଛି ଇଣ୍ଟିଜର୍ Z ର ରିଙ୍ଗ, ଏହି ଅନ୍ତର୍ନିହିତତା ଏକ ଆଦର୍ଶ ସହିତ ଦେଖାଯାଉଥିବା ମୂଖ୍ୟ ଆଦର୍ଶ ସ୍ପେକ୍ଟ୍ରମ୍ ସ୍ପେକ୍ ( Z ) ଉପରେ ନିର୍ଭର କରେ | ଆରିଥମେଟିକ୍ ପୃଷ୍ଠଗୁଡ଼ିକ ଡାଇଓଫାଣ୍ଟାଇନ୍ ଜ୍ୟାମିତୀରେ ସ୍ natural ାଭାବିକ ଭାବରେ ଉତ୍ପନ୍ନ ହୁଏ, ଯେତେବେଳେ K ଉପରେ ବ୍ୟାଖ୍ୟା କରାଯାଇଥିବା ଏକ ବୀଜ ବର୍ଣ୍ଣିତ ବକ୍ର R / P କ୍ଷେତ୍ର ଉପରେ ହ୍ରାସ ବୋଲି ଚିନ୍ତା କରାଯାଏ, ଯେଉଁଠାରେ P R ର ଏକ ଆଦର୍ଶ ଅଟେ, ପ୍ରାୟ ସମସ୍ତ P ପାଇଁ ; ଏବଂ R / P କୁ ହ୍ରାସ କରିବାର ପ୍ରକ୍ରିୟା ବିଷୟରେ କ'ଣ ଘଟିବା ଉଚିତ ତାହା ନିର୍ଦ୍ଧିଷ୍ଟ କରିବାରେ ସହାୟକ ହୋଇଥାଏ ଯେତେବେଳେ ଅତ୍ୟନ୍ତ ନିର୍ବୋଧ ଉପାୟ ବୁ sense ିବାରେ ବିଫଳ ହୁଏ |
ଗାଣିତିକ ଟପୋଲୋଜି: ଗାଣିତିକ ଟପୋଲୋଜି ହେଉଛି ଗଣିତର ଏକ କ୍ଷେତ୍ର ଯାହା ବୀଜ ବର୍ଣ୍ଣିତ ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତ ଏବଂ ଟପୋଲୋଜିର ଏକ ମିଶ୍ରଣ | ଏହା ସଂଖ୍ୟା କ୍ଷେତ୍ର ଏବଂ ବନ୍ଦ, ଆଭିମୁଖ୍ୟ 3-ମେନିଫୋଲ୍ଡ ମଧ୍ୟରେ ଏକ ସମାନତା ପ୍ରତିଷ୍ଠା କରେ |
କକ୍ସଟର - ଡିନକିନ୍ ଚିତ୍ର: ଜ୍ୟାମିତୀରେ , ଏକ କକ୍ସେଟର୍ - ଡିନକିନ୍ ଚିତ୍ର ହେଉଛି ଏକ ଗ୍ରାଫ୍ ଯାହା ସାଂଖ୍ୟିକ ଭାବରେ ଲେବଲ୍ ହୋଇଥିବା ଧାର ସହିତ ଦର୍ପଣ ସଂଗ୍ରହ ମଧ୍ୟରେ ସ୍ଥାନିକ ସମ୍ପର୍କକୁ ପ୍ରତିନିଧିତ୍ୱ କରେ | ଏହା ଏକ କାଲିଡୋସ୍କୋପିକ୍ ନିର୍ମାଣକୁ ବର୍ଣ୍ଣନା କରେ: ପ୍ରତ୍ୟେକ ଗ୍ରାଫ୍ "ନୋଡ୍" ଏକ ଦର୍ପଣକୁ ପ୍ରତିପାଦିତ କରେ ଏବଂ ଏକ ଶାଖା ସହିତ ସଂଲଗ୍ନ ହୋଇଥିବା ଲେବଲ୍ ଦୁଇଟି ଦର୍ପଣ ମଧ୍ୟରେ ଡାଇହେଡ୍ରାଲ୍ ଆଙ୍ଗଲ୍ କ୍ରମକୁ ଏନକୋଡ୍ କରେ, ଅର୍ଥାତ୍ ପ୍ରତିଫଳିତ ବିମାନଗୁଡ଼ିକ ମଧ୍ୟରେ କୋଣକୁ 180 ପାଇବାକୁ ଗୁଣ କରାଯାଇପାରେ | ଡିଗ୍ରୀ ଏକ ଅବ୍ୟବହୃତ ଶାଖା କ୍ରମାଗତ ଭାବରେ ଅର୍ଡର -3 କୁ ପ୍ରତିନିଧିତ୍ୱ କରେ |
ଗାଣିତିକ ଅଣ୍ଡରଫ୍ଲୋ: ଆରିଥମେଟିକ୍ ଅଣ୍ଡରଫ୍ଲୋ ଶବ୍ଦ ହେଉଛି ଏକ କମ୍ପ୍ୟୁଟର ପ୍ରୋଗ୍ରାମର ଏକ ଅବସ୍ଥା ଯେଉଁଠାରେ ଏକ ଗଣନର ଫଳାଫଳ ଅନେକ ଛୋଟ ସଂପୂର୍ଣ୍ଣ ମୂଲ୍ୟ ଅଟେ, କମ୍ପ୍ୟୁଟର ପ୍ରକୃତରେ ଏହାର କେନ୍ଦ୍ରୀୟ ପ୍ରକ୍ରିୟାକରଣ ୟୁନିଟ୍ (CPU) ରେ ସ୍ମୃତିରେ ପ୍ରତିନିଧିତ୍ୱ କରିପାରିବ |
ଗାଣିତିକ ବିବିଧତା: ଗଣିତରେ, ଏକ ଗାଣିତିକ ବିବିଧତା ହେଉଛି ହର୍ମିଟିଆନ୍ ସମୃଦ୍ଧ ସ୍ଥାନର ସହଭାଗୀ ବୀଜ ବର୍ଣ୍ଣିତ ମିଛ ଗୋଷ୍ଠୀର ଏକ ଆରିଥମେଟିକ୍ ସବ୍ ଗ୍ରୁପ୍ ଦ୍ୱାରା |
ଗାଣିତିକ ବିବିଧତା: ଗଣିତରେ, ଏକ ଗାଣିତିକ ବିବିଧତା ହେଉଛି ହର୍ମିଟିଆନ୍ ସମୃଦ୍ଧ ସ୍ଥାନର ସହଭାଗୀ ବୀଜ ବର୍ଣ୍ଣିତ ମିଛ ଗୋଷ୍ଠୀର ଏକ ଆରିଥମେଟିକ୍ ସବ୍ ଗ୍ରୁପ୍ ଦ୍ୱାରା |
ଗାଣିତିକ ଜେଟା କାର୍ଯ୍ୟ: ଗଣିତରେ, ଗାଣିତିକ ଜେଟା ଫଙ୍କସନ୍ ହେଉଛି ଏକ ଜେଟା ଫଙ୍କସନ୍ ଯାହା ଇଣ୍ଟିଜର୍ସ ଉପରେ ସୀମିତ ପ୍ରକାରର ସ୍କିମ୍ ସହିତ ଜଡିତ | ଗାଣିତିକ ଜେଟା ଫଙ୍କସନ୍ ରିମାନ୍ ଜେଟା ଫଙ୍କସନ୍ ଏବଂ ଡେଡେକିଣ୍ଡ ଜେଟା ଫଙ୍କସନ୍ କୁ ଉଚ୍ଚ ଆକାରରେ ସାଧାରଣ କରିଥାଏ | ଗାଣିତିକ ଜେଟା ଫଙ୍କସନ୍ ହେଉଛି ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତର ଅନ୍ୟତମ ମ fundamental ଳିକ ବସ୍ତୁ |
ଗାଣିତିକ: ଆରିଥମେଟିକା ହେଉଛି ଗଣିତ ଉପରେ ଏକ ପ୍ରାଚୀନ ଗ୍ରୀକ୍ ପାଠ ଯାହାକି ଖ୍ରୀଷ୍ଟାବ୍ଦ ତୃତୀୟ ଶତାବ୍ଦୀରେ ଗଣିତଜ୍ଞ ଡାୟୋଫାଣ୍ଟସ୍ଙ୍କ ଦ୍ୱାରା ଲିଖିତ | ଏହା 130 ସମୀକରଣ ସମସ୍ୟାର ଏକ ସଂଗ୍ରହ ଅଟେ ଯାହା ନିର୍ଣ୍ଣୟ ସମୀକରଣ ଏବଂ ନିର୍ଦ୍ଦିଷ୍ଟ ସମୀକରଣର ସାଂଖ୍ୟିକ ସମାଧାନ ପ୍ରଦାନ କରେ |
ଜନ ୱାଲିସ୍: ଜନ୍ ୱାଲିସ୍ ଜଣେ ଇଂରାଜୀ ଧର୍ମଗୁରୁ ତଥା ଗଣିତଜ୍ଞ ଥିଲେ ଯିଏ ଅସୀମ କାଲକୁଲସ୍ ବିକାଶ ପାଇଁ ଆଂଶିକ ଶ୍ରେୟ ପ୍ରଦାନ କରିଥିଲେ | 1643 ରୁ 1689 ମଧ୍ୟରେ ସେ ସଂସଦ ଏବଂ ପରେ ରାଜକୀୟ ପାଇଁ ମୁଖ୍ୟ କ୍ରିପ୍ଟୋଗ୍ରାଫର ଭାବରେ କାର୍ଯ୍ୟ କରିଥିଲେ | ଅସୀମତାର ସଂକଳ୍ପକୁ ପ୍ରତିପାଦନ କରିବା ପାଇଁ ସେ ପ୍ରତୀକ ପରିଚୟ ଦେଇ ଶ୍ରେୟସ୍କର | ସେ ସମାନ ଭାବରେ ଏକ ଅସୀମ ପାଇଁ 1 / used ବ୍ୟବହାର କଲେ | ଜନ୍ ୱାଲିସ୍ ନ୍ୟୁଟନ୍ ର ସମକାଳୀନ ଏବଂ ଗଣିତର ପ୍ରାରମ୍ଭିକ ପୁନ na ନିର୍ମାଣର ଶ୍ରେଷ୍ଠ ବୁଦ୍ଧିଜୀବୀ ଥିଲେ |
ହେନେରୀ ବ୍ରିଗ୍ଗସ୍ (ଗଣିତଜ୍ଞ): ହେନେରୀ ବ୍ରିଗ୍ଗସ୍ ଜଣେ ଇଂରାଜୀ ଗଣିତଜ୍ଞ ଥିଲେ, ଜନ୍ ନାପିଅର୍ଙ୍କ ଦ୍ ven ାରା ଉଦ୍ଭାବିତ ମୂଳ ଲୋଗାରିଦମକୁ ସାଧାରଣ ଲୋଗାରିଦମରେ ପରିଣତ କରିବା ପାଇଁ ଉଲ୍ଲେଖନୀୟ ଥିଲେ, ଯାହା ତାଙ୍କ ସମ୍ମାନରେ ବ୍ରିଗସିୟାନ୍ ଲୋଗାରିଦମ ଭାବରେ ଜଣାଶୁଣା | ଆଧୁନିକ ବ୍ୟବହାରରେ ଦୀର୍ଘ ବିଭାଜନ ପାଇଁ ନିର୍ଦ୍ଦିଷ୍ଟ ଆଲଗୋରିଦମ ବ୍ରିଗସ୍ ସି ଦ୍ୱାରା ପ୍ରବର୍ତ୍ତିତ ହୋଇଥିଲା | 1600 ଖ୍ରୀଷ୍ଟ
ଆରିଥମେଟିକା ୟୁନିଭର୍ଲିସ୍: ଆରିଥମେଟିକା ୟୁନିଭର୍ଲିସ୍ ହେଉଛି ଆଇଜାକ୍ ନ୍ୟୁଟନ୍ଙ୍କ ଏକ ଗଣିତ ପାଠ୍ୟ | ଲାଟିନ୍ ଭାଷାରେ ଲିଖିତ, ଏହାକୁ କେମ୍ବ୍ରିଜ୍ ବିଶ୍ୱବିଦ୍ୟାଳୟର ଗଣିତର ଲୁକାସିଆନ୍ ପ୍ରଫେସର ଭାବରେ ନ୍ୟୁଟନ୍ଙ୍କ ଉତ୍ତରାଧିକାରୀ ୱିଲିୟମ୍ ହ୍ୱିଷ୍ଟନ୍ ସମ୍ପାଦନା କରି ପ୍ରକାଶ କରିଥିଲେ। ଆରିଥମେଟିକା ନ୍ୟୁଟନ୍ଙ୍କ ବକ୍ତୃତା ନୋଟ୍ ଉପରେ ଆଧାରିତ ଥିଲା |
ଦଶ ଗଣନାକାରୀ କାନନ୍: ଦଶ ଗଣନାକାରୀ କାନନ୍ ଦଶଟି ଚାଇନିଜ୍ ଗାଣିତିକ କାର୍ଯ୍ୟର ଏକ ସଂଗ୍ରହ ଥିଲା, ଯାହା ଟାଙ୍ଗ୍ ରାଜବଂଶର ଗଣିତଜ୍ଞ ଲି ଚୁନ୍ଫେଙ୍ଗ୍ (602-670) ଙ୍କ ଦ୍ iled ାରା ଗଣିତରେ ସାମ୍ରାଜ୍ୟ ପରୀକ୍ଷା ପାଇଁ ସରକାରୀ ଗାଣିତିକ ଗ୍ରନ୍ଥ ଭାବରେ ସଂକଳିତ ହୋଇଥିଲା |
ଦ୍ୱିତୀୟ କ୍ରମ ଗଣିତ: ଗାଣିତିକ ତର୍କରେ, ଦ୍ୱିତୀୟ କ୍ରମାଙ୍କ ଗଣିତ ହେଉଛି ସ୍ୱୀକୃତିପ୍ରାପ୍ତ ପ୍ରଣାଳୀର ଏକ ସଂଗ୍ରହ ଯାହା ପ୍ରାକୃତିକ ସଂଖ୍ୟା ଏବଂ ସେମାନଙ୍କର ସବ୍ସେଟ୍କୁ formal ପଚାରିକ କରିଥାଏ | ଗଣିତର ଅନେକ ପାଇଁ ମୂଳଦୁଆ ଭାବରେ ଆକ୍ସିଓମେଟିକ୍ ସେଟ୍ ସିଦ୍ଧାନ୍ତ ପାଇଁ ଏହା ଏକ ବିକଳ୍ପ |
ଜର୍ଜ ପାଇକ: ଜର୍ଜ ପାଇକ FRS ଜଣେ ଇଂରାଜୀ ଗଣିତଜ୍ଞ ଏବଂ ଅଙ୍ଗଲିକାନ୍ ଧର୍ମଗୁରୁ ଥିଲେ | ଯାହାକୁ ତର୍କର ବ୍ରିଟିଶ ବୀଜ ବିବେଚନା କୁହାଯାଏ ସେ ପ୍ରତିଷ୍ଠା କରିଥିଲେ।
ଗାଣିତିକ ଜ୍ୟାମିତି: ଗଣିତରେ, ଗାଣିତିକ ଜ୍ୟାମିତି ପ୍ରାୟତ al ବୀଜ ବର୍ଣ୍ଣିତ ଜ୍ୟାମିତିରୁ ସଂଖ୍ୟା ତତ୍ତ୍ problems ର ସମସ୍ୟା ପର୍ଯ୍ୟନ୍ତ କ techni ଶଳର ପ୍ରୟୋଗ ଅଟେ | ଆରିଥମେଟିକ୍ ଜ୍ୟାମିତ୍ରୀ ଡାୟୋଫାଣ୍ଟାଇନ୍ ଜ୍ୟାମିତିର ଚାରିପାଖରେ କେନ୍ଦ୍ରୀଭୂତ ହୋଇଛି, ବୀଜ ବର୍ଣ୍ଣିତ କିସମର ଯୁକ୍ତିଯୁକ୍ତ ବିନ୍ଦୁ ଅଧ୍ୟୟନ |
ଗାଣିତିକ ତର୍କ ଏକକ: ଗଣନାରେ, ଏକ ଆରିଥମେଟିକ୍ ଲଜିକ୍ ୟୁନିଟ୍ (ALU) ହେଉଛି ଏକ ମିଳିତ ଡିଜିଟାଲ୍ ସର୍କିଟ୍ ଯାହା ଇଣ୍ଟିଜର୍ ବାଇନାରୀ ନମ୍ବର ଉପରେ ଗାଣିତିକ ଏବଂ ବିଟୱାଇସ୍ ଅପରେସନ୍ କରିଥାଏ | ଏହା ଏକ ଫ୍ଲୋଟିଂ ପଏଣ୍ଟ ୟୁନିଟ୍ (FPU) ର ବିପରୀତ, ଯାହା ଫ୍ଲୋଟିଂ ପଏଣ୍ଟ ନମ୍ବର ଉପରେ କାର୍ଯ୍ୟ କରେ | ଏହା କମ୍ପ୍ୟୁଟର, FPU ଏବଂ ଗ୍ରାଫିକ୍ସ ପ୍ରକ୍ରିୟାକରଣ ୟୁନିଟ୍ (ଜିପିୟୁ) ର କେନ୍ଦ୍ରୀୟ ପ୍ରକ୍ରିୟାକରଣ ୟୁନିଟ୍ (CPU) ଅନ୍ତର୍ଭୂକ୍ତ କରି ଅନେକ ପ୍ରକାରର ଗଣନା ସର୍କିଟ୍ ର ଏକ ମ fundamental ଳିକ ବିଲ୍ଡିଂ ବ୍ଲକ୍ |
ଦ୍ୱିତୀୟ କ୍ରମ ଗଣିତ: ଗାଣିତିକ ତର୍କରେ, ଦ୍ୱିତୀୟ କ୍ରମାଙ୍କ ଗଣିତ ହେଉଛି ସ୍ୱୀକୃତିପ୍ରାପ୍ତ ପ୍ରଣାଳୀର ଏକ ସଂଗ୍ରହ ଯାହା ପ୍ରାକୃତିକ ସଂଖ୍ୟା ଏବଂ ସେମାନଙ୍କର ସବ୍ସେଟ୍କୁ formal ପଚାରିକ କରିଥାଏ | ଗଣିତର ଅନେକ ପାଇଁ ମୂଳଦୁଆ ଭାବରେ ଆକ୍ସିଓମେଟିକ୍ ସେଟ୍ ସିଦ୍ଧାନ୍ତ ପାଇଁ ଏହା ଏକ ବିକଳ୍ପ |
ଦ୍ୱିତୀୟ କ୍ରମ ଗଣିତ: ଗାଣିତିକ ତର୍କରେ, ଦ୍ୱିତୀୟ କ୍ରମାଙ୍କ ଗଣିତ ହେଉଛି ସ୍ୱୀକୃତିପ୍ରାପ୍ତ ପ୍ରଣାଳୀର ଏକ ସଂଗ୍ରହ ଯାହା ପ୍ରାକୃତିକ ସଂଖ୍ୟା ଏବଂ ସେମାନଙ୍କର ସବ୍ସେଟ୍କୁ formal ପଚାରିକ କରିଥାଏ | ଗଣିତର ଅନେକ ପାଇଁ ମୂଳଦୁଆ ଭାବରେ ଆକ୍ସିଓମେଟିକ୍ ସେଟ୍ ସିଦ୍ଧାନ୍ତ ପାଇଁ ଏହା ଏକ ବିକଳ୍ପ |
ବିସ୍ତୃତ ଆନାଲିଟିକ୍ ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତ: ଅବଷ୍ଟ୍ରାକ୍ଟ ଆନାଲିଟିକ୍ ନମ୍ବର ସିଦ୍ଧାନ୍ତ ହେଉଛି ଗଣିତର ଏକ ଶାଖା ଯାହା ଶାସ୍ତ୍ରୀୟ ଆନାଲିଟିକ୍ ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତର ଧାରଣା ଏବଂ କ ques ଶଳକୁ ନେଇଥାଏ ଏବଂ ଏହାକୁ ବିଭିନ୍ନ ଗାଣିତିକ କ୍ଷେତ୍ରରେ ପ୍ରୟୋଗ କରିଥାଏ | ଶାସ୍ତ୍ରୀୟ ପ୍ରାଇମ୍ ନମ୍ବର ଥିଓରେମ୍ ଏକ ପ୍ରୋଟୋଟାଇପିକାଲ୍ ଉଦାହରଣ ଭାବରେ କାର୍ଯ୍ୟ କରେ, ଏବଂ ଅବଷ୍ଟ୍ରାକ୍ଟ ଅସ୍ମିପଟୋଟିକ୍ ବଣ୍ଟନ ଫଳାଫଳ ଉପରେ ଗୁରୁତ୍ୱ ଦିଆଯାଇଛି | ବିଂଶ ଶତାବ୍ଦୀରେ ଜନ୍ ନୋପଫମାଚର୍ ଏବଂ ଆର୍ନ ବେର୍ଲିଙ୍ଗଙ୍କ ପରି ଗଣିତଜ୍ଞଙ୍କ ଦ୍ The ାରା ଏହି ସିଦ୍ଧାନ୍ତ ଉଦ୍ଭାବନ କରାଯାଇଥିଲା ଏବଂ ବିକଶିତ ହୋଇଥିଲା |
ଗାଣିତିକ କାର୍ଯ୍ୟ: ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତରେ, ଏକ ଗାଣିତିକ , ଗାଣିତିକ , କିମ୍ବା ସଂଖ୍ୟା-ତତ୍ତ୍ୱିକ କାର୍ଯ୍ୟ ଅଧିକାଂଶ ଲେଖକଙ୍କ ପାଇଁ ଯେକ any ଣସି କାର୍ଯ୍ୟ f ( n ) ଯାହାର ଡୋମେନ୍ ସକରାତ୍ମକ ପୂର୍ଣ୍ଣ ସଂଖ୍ୟା ଏବଂ ଯାହାର ପରିସର ଜଟିଳ ସଂଖ୍ୟାଗୁଡ଼ିକର ଉପସେଟ ଅଟେ | ହାର୍ଡି ଏବଂ ରାଇଟ୍ ସେମାନଙ୍କର ପରିଭାଷାରେ ଆବଶ୍ୟକତାକୁ ଅନ୍ତର୍ଭୁକ୍ତ କରନ୍ତି ଯେ ଏକ ଗାଣିତିକ କାର୍ଯ୍ୟ " n ର କିଛି ଗାଣିତିକ ଗୁଣ ପ୍ରକାଶ କରେ" |
ଗାଣିତିକ କାର୍ଯ୍ୟ: ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତରେ, ଏକ ଗାଣିତିକ , ଗାଣିତିକ , କିମ୍ବା ସଂଖ୍ୟା-ତତ୍ତ୍ୱିକ କାର୍ଯ୍ୟ ଅଧିକାଂଶ ଲେଖକଙ୍କ ପାଇଁ ଯେକ any ଣସି କାର୍ଯ୍ୟ f ( n ) ଯାହାର ଡୋମେନ୍ ସକରାତ୍ମକ ପୂର୍ଣ୍ଣ ସଂଖ୍ୟା ଏବଂ ଯାହାର ପରିସର ଜଟିଳ ସଂଖ୍ୟାଗୁଡ଼ିକର ଉପସେଟ ଅଟେ | ହାର୍ଡି ଏବଂ ରାଇଟ୍ ସେମାନଙ୍କର ପରିଭାଷାରେ ଆବଶ୍ୟକତାକୁ ଅନ୍ତର୍ଭୁକ୍ତ କରନ୍ତି ଯେ ଏକ ଗାଣିତିକ କାର୍ଯ୍ୟ " n ର କିଛି ଗାଣିତିକ ଗୁଣ ପ୍ରକାଶ କରେ" |
ଗାଣିତିକ କ୍ରମ: ଗାଣିତିକ ତର୍କ ରେ, arithmetical ଅନୁକ୍ରମ, ଗାଣିତିକ ଅନୁକ୍ରମ କିମ୍ବା Kleene-Mostowski ଅନୁକ୍ରମ ସେମାନଙ୍କୁ ବ୍ୟାଖ୍ୟା ଯେ ସୂତ୍ର ଜଟିଳତାକୁ ଉପରେ ଆଧାରିତ ନିର୍ଦ୍ଦିଷ୍ଟ େସଟଗୁଡ଼ିକ classifies। ଯେକ Any ଣସି ସେଟ୍ ଯାହା ଏକ ଶ୍ରେଣୀକରଣ ଗ୍ରହଣ କରେ ଏହାକୁ ଗଣିତ କୁହାଯାଏ |
ଗାଣିତିକ ଅର୍ଥ: ଗଣିତ ଏବଂ ପରିସଂଖ୍ୟାନରେ, ଗାଣିତିକ ଅର୍ଥ , କିମ୍ବା କେବଳ ଅର୍ଥ ବା ହାରାହାରି , ସଂଗ୍ରହରେ ସଂଖ୍ୟା ଗଣନା ଦ୍ୱାରା ବିଭକ୍ତ ସଂଖ୍ୟା ସଂଗ୍ରହର ସମଷ୍ଟି ଅଟେ | ସଂଗ୍ରହ ପ୍ରାୟତ an ଏକ ପରୀକ୍ଷଣ କିମ୍ବା ପର୍ଯ୍ୟବେକ୍ଷଣଶୀଳ ଅଧ୍ୟୟନର ଫଳାଫଳର ଏକ ସେଟ୍, କିମ୍ବା ବାରମ୍ବାର ଏକ ସର୍ବେକ୍ଷଣରୁ ଫଳାଫଳର ଏକ ସେଟ୍ | ଗଣିତ ଏବଂ ପରିସଂଖ୍ୟାନରେ କେତେକ ପ୍ରସଙ୍ଗରେ "ଗାଣିତିକ ଅର୍ଥ" ଶବ୍ଦକୁ ଅଧିକ ପସନ୍ଦ କରାଯାଏ, କାରଣ ଏହା ଏହାକୁ ଅନ୍ୟ ଉପାୟଠାରୁ ଭିନ୍ନ କରିବାରେ ସାହାଯ୍ୟ କରିଥାଏ, ଯେପରିକି ଜ୍ୟାମିତିକ ଅର୍ଥ ଏବଂ ହାରମୋନିକ୍ ଅର୍ଥ |
ଗାଣିତିକ ସେଟ୍: ଗାଣିତିକ ତର୍କରେ, ଏକ ଗାଣିତିକ ସେଟ୍ ହେଉଛି ପ୍ରାକୃତିକ ସଂଖ୍ୟାଗୁଡ଼ିକର ଏକ ସେଟ୍ ଯାହା ପ୍ରଥମ କ୍ରମର ପିଆନୋ ଗାଣିତିକର ଏକ ସୂତ୍ର ଦ୍ୱାରା ବ୍ୟାଖ୍ୟା କରାଯାଇପାରେ | ଗାଣିତିକ ସେଟ୍ ଗୁଡିକ ଗାଣିତିକ କ୍ରମବଦ୍ଧତା ଦ୍ୱାରା ବର୍ଗୀକୃତ |
ଗାଣିତିକ ସେଟ୍: ଗାଣିତିକ ତର୍କରେ, ଏକ ଗାଣିତିକ ସେଟ୍ ହେଉଛି ପ୍ରାକୃତିକ ସଂଖ୍ୟାଗୁଡ଼ିକର ଏକ ସେଟ୍ ଯାହା ପ୍ରଥମ କ୍ରମର ପିଆନୋ ଗାଣିତିକର ଏକ ସୂତ୍ର ଦ୍ୱାରା ବ୍ୟାଖ୍ୟା କରାଯାଇପାରେ | ଗାଣିତିକ ସେଟ୍ ଗୁଡିକ ଗାଣିତିକ କ୍ରମବଦ୍ଧତା ଦ୍ୱାରା ବର୍ଗୀକୃତ |
ଗାଣିତିକ: ଆରିଥମେଟିକ୍ ହେଉଛି ଗଣିତର ଏକ ଶାଖା ଯାହା ସଂଖ୍ୟାଗୁଡ଼ିକର ଅଧ୍ୟୟନକୁ ନେଇ ଗଠିତ, ବିଶେଷତ them ସେମାନଙ୍କ ଉପରେ ପାରମ୍ପାରିକ କାର୍ଯ୍ୟର ଗୁଣ - ଯୋଗ, ବିତରଣ, ଗୁଣନ, ବିଭାଜନ, ମୂଳ ଏବଂ ନିର୍ବାହ | ଆରିଥମେଟିକ୍ ହେଉଛି ସଂଖ୍ୟା ତତ୍ତ୍ an ର ଏକ ପ୍ରାଥମିକ ଅଂଶ, ଏବଂ ସଂଖ୍ୟା ଥିଓରୀକୁ ଆଧୁନିକ ଗଣିତର ଏକ ଉଚ୍ଚ ସ୍ତରୀୟ ବିଭାଗ ଭାବରେ ବିବେଚନା କରାଯାଏ, ବୀଜ୍, ଜ୍ୟାମିତି ଏବଂ ବିଶ୍ଳେଷଣ ସହିତ | ଆରିଥମେଟିକ୍ ଏବଂ ଉଚ୍ଚ ଆରିଥମେଟିକ୍ ଶବ୍ଦଗୁଡିକ ବିଂଶ ଶତାବ୍ଦୀର ଆରମ୍ଭ ପର୍ଯ୍ୟନ୍ତ ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତର ସମକକ୍ଷ ଭାବରେ ବ୍ୟବହୃତ ହୋଇଥିଲା ଏବଂ ବେଳେବେଳେ ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତର ଏକ ବ୍ୟାପକ ଅଂଶକୁ ସୂଚାଇବା ପାଇଁ ବ୍ୟବହୃତ ହୁଏ |
ଗାଣିତିକ ପ୍ରଗତି: ଏକ ଆରିଥମେଟିକ୍ ପ୍ରଗତି (AP) ବା ଗାଣିତିକ କ୍ରମ ହେଉଛି ସଂଖ୍ୟାଗୁଡ଼ିକର କ୍ରମ ଯେପରି କ୍ରମାଗତ ଶବ୍ଦଗୁଡ଼ିକ ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ ସ୍ଥିର ଅଟେ | ଉଦାହରଣ ସ୍ୱରୂପ, କ୍ରମ 5, 7, 9, 11, 13, 15 ,। 2 ର ସାଧାରଣ ପାର୍ଥକ୍ୟ ସହିତ ଏକ ଗାଣିତିକ ପ୍ରଗତି |
Otonality ଏବଂ Utonality: ଓଟୋନାଲିଟି ଏବଂ ଉଟୋନାଲିଟି ଶବ୍ଦଗୁଡିକ ହ୍ୟାରି ପାର୍ଟଙ୍କ ଦ୍ introduced ାରା ପ୍ରବର୍ତ୍ତିତ ଶବ୍ଦଗୁଡିକ ବର୍ଣ୍ଣନା କରିବାକୁ ଯାହାର ପିଚ୍ ଶ୍ରେଣୀଗୁଡ଼ିକ ଯଥାକ୍ରମେ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ସ୍ୱର (ପରିଚୟ) ର ହାରମୋନିକ୍ସ ବା ସବହର୍ମୋନିକ୍ସ | ଉଦାହରଣ ସ୍ୱରୂପ: 1/1, 2/1, 3/1, ... କିମ୍ବା 1/1, 1/2, 1/3, .... ଏକ ଓଟୋନାଲିଟି ହେଉଛି ସାଂଖ୍ୟିକ କାରକ (... ପରିଚୟ ) ଦ୍ ated ାରା ସୃଷ୍ଟି ହୋଇଥିବା ପିଚ୍ ସେଟ୍ ... ନାମରେ ଏକ ସାଂଖ୍ୟିକ ସ୍ଥିର ଉପରେ | ଅପରପକ୍ଷେ, ଏକ ଉଟୋନାଲିଟି ହେଉଛି ଏକ ଓଟୋନାଲିଟିର ବିପରୀତତା, ସାଂଖ୍ୟିକ କାରଣଗୁଡ଼ିକ ଉପରେ ସଂଖ୍ୟାରେ ଏକ ସାଂଖ୍ୟିକ ସ୍ଥିର ସହିତ ପିଚ୍ ସେଟ୍ ... ନାମରେ |
ଗାଣିତିକ ସେଟ୍: ଗାଣିତିକ ତର୍କରେ, ଏକ ଗାଣିତିକ ସେଟ୍ ହେଉଛି ପ୍ରାକୃତିକ ସଂଖ୍ୟାଗୁଡ଼ିକର ଏକ ସେଟ୍ ଯାହା ପ୍ରଥମ କ୍ରମର ପିଆନୋ ଗାଣିତିକର ଏକ ସୂତ୍ର ଦ୍ୱାରା ବ୍ୟାଖ୍ୟା କରାଯାଇପାରେ | ଗାଣିତିକ ସେଟ୍ ଗୁଡିକ ଗାଣିତିକ କ୍ରମବଦ୍ଧତା ଦ୍ୱାରା ବର୍ଗୀକୃତ |
ଗାଣିତିକ କ୍ରମ: ଗାଣିତିକ ତର୍କ ରେ, arithmetical ଅନୁକ୍ରମ, ଗାଣିତିକ ଅନୁକ୍ରମ କିମ୍ବା Kleene-Mostowski ଅନୁକ୍ରମ ସେମାନଙ୍କୁ ବ୍ୟାଖ୍ୟା ଯେ ସୂତ୍ର ଜଟିଳତାକୁ ଉପରେ ଆଧାରିତ ନିର୍ଦ୍ଦିଷ୍ଟ େସଟଗୁଡ଼ିକ classifies। ଯେକ Any ଣସି ସେଟ୍ ଯାହା ଏକ ଶ୍ରେଣୀକରଣ ଗ୍ରହଣ କରେ ଏହାକୁ ଗଣିତ କୁହାଯାଏ |
ଗାଣିତିକ ରିଙ୍ଗ: ଏକ commutative ମୁଦି R arithmetical ବୋଲି କହିଲେ ହୋଇଥାଏ algebra ରେ, ନିମ୍ନଲିଖିତ ସମାନ ଅବସ୍ଥା ଯେକୌଣସି ଧାରଣ ଯଦି: ଲୋକାଲାଇଜେସନ୍ ର R ରେ ପ୍ରତ୍ୟେକ ସର୍ବାଧିକ ଆଦର୍ଶ ପାଇଁ ଏକ ୟୁନିସେରିଆଲ୍ ରିଙ୍ଗ | R ର ସମସ୍ତ ଆଦର୍ଶ ପାଇଁ | , ଏବଂ , ସମସ୍ତ ଆଦର୍ଶ ପାଇଁ | , ଏବଂ ,
ଗାଣିତିକ ସେଟ୍: ଗାଣିତିକ ତର୍କରେ, ଏକ ଗାଣିତିକ ସେଟ୍ ହେଉଛି ପ୍ରାକୃତିକ ସଂଖ୍ୟାଗୁଡ଼ିକର ଏକ ସେଟ୍ ଯାହା ପ୍ରଥମ କ୍ରମର ପିଆନୋ ଗାଣିତିକର ଏକ ସୂତ୍ର ଦ୍ୱାରା ବ୍ୟାଖ୍ୟା କରାଯାଇପାରେ | ଗାଣିତିକ ସେଟ୍ ଗୁଡିକ ଗାଣିତିକ କ୍ରମବଦ୍ଧତା ଦ୍ୱାରା ବର୍ଗୀକୃତ |
ଓଲଟା ଗଣିତ: ଓଲଟା ଗଣିତ ହେଉଛି ଗାଣିତିକ ତର୍କର ଏକ ପ୍ରୋଗ୍ରାମ୍ ଯାହା ଗଣିତର ତତ୍ତ୍ prove ପ୍ରମାଣ କରିବାକୁ କେଉଁ ଆକ୍ସିୟମ୍ ଆବଶ୍ୟକ ତାହା ନିର୍ଣ୍ଣୟ କରିବାକୁ ଚେଷ୍ଟା କରେ | ଏହାର ପରିଭାଷିତ ପଦ୍ଧତିକୁ ସଂକ୍ଷେପରେ ବର୍ଣ୍ଣନା କରାଯାଇପାରେ ଯେ ଆକ୍ସିଓମରୁ ଥିଓରେମଗୁଡିକ ପ୍ରାପ୍ତ କରିବାର ସାଧାରଣ ଗାଣିତିକ ଅଭ୍ୟାସର ବିପରୀତ ଭାବରେ, "ଥିଓରେମ୍ ଠାରୁ ଆକ୍ସିଓମ୍ କୁ ପଛକୁ ଯିବା" ଭାବରେ ବର୍ଣ୍ଣନା କରାଯାଇପାରେ | ପର୍ଯ୍ୟାପ୍ତ ପରିସ୍ଥିତିରୁ ଆବଶ୍ୟକ ସର୍ତ୍ତଗୁଡିକ ସ୍କଲପ୍ କରିବା ପରି ଏହାକୁ ଧାରଣା କରାଯାଇପାରେ |
ଗାଣିତିକ ସେଟ୍: ଗାଣିତିକ ତର୍କରେ, ଏକ ଗାଣିତିକ ସେଟ୍ ହେଉଛି ପ୍ରାକୃତିକ ସଂଖ୍ୟାଗୁଡ଼ିକର ଏକ ସେଟ୍ ଯାହା ପ୍ରଥମ କ୍ରମର ପିଆନୋ ଗାଣିତିକର ଏକ ସୂତ୍ର ଦ୍ୱାରା ବ୍ୟାଖ୍ୟା କରାଯାଇପାରେ | ଗାଣିତିକ ସେଟ୍ ଗୁଡିକ ଗାଣିତିକ କ୍ରମବଦ୍ଧତା ଦ୍ୱାରା ବର୍ଗୀକୃତ |
ଗାଣିତିକ ସେଟ୍: ଗାଣିତିକ ତର୍କରେ, ଏକ ଗାଣିତିକ ସେଟ୍ ହେଉଛି ପ୍ରାକୃତିକ ସଂଖ୍ୟାଗୁଡ଼ିକର ଏକ ସେଟ୍ ଯାହା ପ୍ରଥମ କ୍ରମର ପିଆନୋ ଗାଣିତିକର ଏକ ସୂତ୍ର ଦ୍ୱାରା ବ୍ୟାଖ୍ୟା କରାଯାଇପାରେ | ଗାଣିତିକ ସେଟ୍ ଗୁଡିକ ଗାଣିତିକ କ୍ରମବଦ୍ଧତା ଦ୍ୱାରା ବର୍ଗୀକୃତ |
ଡେଡେକିଣ୍ଡ ଜେଟା କାର୍ଯ୍ୟ: ରେ ଗଣିତ, ଏକ algebraic ସଂଖ୍ଯା କ୍ଷେତ୍ର କେ Dedekind zeta ଫଳନ, ସାଧାରଣତଃ ζ K (ଗୁଡିକ) ଅବଧାରଣା, Riemann zeta ଫଙ୍କସନ୍ ଏକ generalization ଅଟେ। ଏହାକୁ ଏକ ଡାଇରିଚଲେଟ୍ ସିରିଜ୍ ଭାବରେ ବ୍ୟାଖ୍ୟା କରାଯାଇପାରେ, ଏହାର ଏକ ଇଉଲର୍ ଉତ୍ପାଦ ବିସ୍ତାର ଅଛି, ଏହା ଏକ କାର୍ଯ୍ୟକଳାପ ସମୀକରଣକୁ ସନ୍ତୁଷ୍ଟ କରେ, ଏହାର ଜଟିଳ ବିମାନ C ରେ ଏକ ମେରୋମର୍ଫିକ୍ ଫଙ୍କସନ୍ ପାଇଁ ଏକ ଆନାଲିଟିକ୍ ଜାରି ରହିଛି, କେବଳ s = 1 ରେ ଏକ ସରଳ ପୋଲ ସହିତ ଏହାର ମୂଲ୍ୟ ଏନକୋଡ୍ | K ର ଗାଣିତିକ ତଥ୍ୟ ବିସ୍ତୃତ Riemann ସେପ୍ଟେମ୍ବର ରାଜ୍ୟ ଯେ ଯଦି ζ K (ଗୁଡିକ) = 0 ଏବଂ 0 <ପୁନଃ (ଗୁଡିକ) <1, ତେବେ Re (ଗୁଡିକ) = 1/2।
ଆରିଥମେଟିକ୍ସ ପ୍ରିନ୍ସିପିଆ, ନୋଭା ପଦ୍ଧତି ଏକ୍ସପୋଜିଟା: ୧ 898989 ର ଗ୍ରନ୍ଥ ଆରିଥମେଟିକ୍ସ ପ୍ରିନ୍ସିୟା, ଜିଉସେପ୍ ପିଆନୋଙ୍କ ନୋଭା ପଦ୍ଧତି ଏକ୍ସପୋଜିଟା ଗାଣିତିକ ତର୍କ ଏବଂ ସେଟ୍ ସିଦ୍ଧାନ୍ତରେ ଏକ ସେମିନାଲ୍ ଡକ୍ୟୁମେଣ୍ଟ୍ ଅଟେ, ଯାହା ବର୍ତ୍ତମାନ ପ୍ରାକୃତିକ ସଂଖ୍ୟାଗୁଡ଼ିକର ମାନକ ଆକ୍ସିଓମାଟାଇଜେସନ୍ ଅଟେ, ଏବଂ ପିଆନୋ ଆକ୍ସିଓମ୍ ଭାବରେ ଜଣାଶୁଣା, ଏବଂ କିଛି ବିସ୍ତାରିତ ନୋଟିସ୍ | ମ basic ଳିକ ସେଟ୍ ଅପରେସନ୍ ପାଇଁ ପ୍ରତୀକ ଭାବରେ ∈, ⊂, ∩, and, ଏବଂ A - B |
ଆରିଥମେଟିକ୍ସ ପ୍ରିନ୍ସିପିଆ, ନୋଭା ପଦ୍ଧତି ଏକ୍ସପୋଜିଟା: ୧ 898989 ର ଗ୍ରନ୍ଥ ଆରିଥମେଟିକ୍ସ ପ୍ରିନ୍ସିୟା, ଜିଉସେପ୍ ପିଆନୋଙ୍କ ନୋଭା ପଦ୍ଧତି ଏକ୍ସପୋଜିଟା ଗାଣିତିକ ତର୍କ ଏବଂ ସେଟ୍ ସିଦ୍ଧାନ୍ତରେ ଏକ ସେମିନାଲ୍ ଡକ୍ୟୁମେଣ୍ଟ୍ ଅଟେ, ଯାହା ବର୍ତ୍ତମାନ ପ୍ରାକୃତିକ ସଂଖ୍ୟାଗୁଡ଼ିକର ମାନକ ଆକ୍ସିଓମାଟାଇଜେସନ୍ ଅଟେ, ଏବଂ ପିଆନୋ ଆକ୍ସିଓମ୍ ଭାବରେ ଜଣାଶୁଣା, ଏବଂ କିଛି ବିସ୍ତାରିତ ନୋଟିସ୍ | ମ basic ଳିକ ସେଟ୍ ଅପରେସନ୍ ପାଇଁ ପ୍ରତୀକ ଭାବରେ ∈, ⊂, ∩, and, ଏବଂ A - B |
ଗାଣିତିକ: ଆରିଥମେଟିକ୍ ହେଉଛି ଗଣିତର ଏକ ଶାଖା ଯାହା ସଂଖ୍ୟାଗୁଡ଼ିକର ଅଧ୍ୟୟନକୁ ନେଇ ଗଠିତ, ବିଶେଷତ them ସେମାନଙ୍କ ଉପରେ ପାରମ୍ପାରିକ କାର୍ଯ୍ୟର ଗୁଣ - ଯୋଗ, ବିତରଣ, ଗୁଣନ, ବିଭାଜନ, ମୂଳ ଏବଂ ନିର୍ବାହ | ଆରିଥମେଟିକ୍ ହେଉଛି ସଂଖ୍ୟା ତତ୍ତ୍ an ର ଏକ ପ୍ରାଥମିକ ଅଂଶ, ଏବଂ ସଂଖ୍ୟା ଥିଓରୀକୁ ଆଧୁନିକ ଗଣିତର ଏକ ଉଚ୍ଚ ସ୍ତରୀୟ ବିଭାଗ ଭାବରେ ବିବେଚନା କରାଯାଏ, ବୀଜ୍, ଜ୍ୟାମିତି ଏବଂ ବିଶ୍ଳେଷଣ ସହିତ | ଆରିଥମେଟିକ୍ ଏବଂ ଉଚ୍ଚ ଆରିଥମେଟିକ୍ ଶବ୍ଦଗୁଡିକ ବିଂଶ ଶତାବ୍ଦୀର ଆରମ୍ଭ ପର୍ଯ୍ୟନ୍ତ ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତର ସମକକ୍ଷ ଭାବରେ ବ୍ୟବହୃତ ହୋଇଥିଲା ଏବଂ ବେଳେବେଳେ ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତର ଏକ ବ୍ୟାପକ ଅଂଶକୁ ସୂଚାଇବା ପାଇଁ ବ୍ୟବହୃତ ହୁଏ |
କଳା କ୍ଷେତ୍ର: ରୋବର୍ଟ ରେକର୍ଡର ଆରିଥମେଟିକ୍ : କିମ୍ବା, ଗ୍ରାଉଣ୍ଡ୍ ଅଫ୍ ଆର୍ଟସ୍ ଗଣିତ ଉପରେ ପ୍ରଥମ ମୁଦ୍ରିତ ଇଂରାଜୀ ପାଠ୍ୟ ପୁସ୍ତକ ମଧ୍ୟରୁ ଗୋଟିଏ ଥିଲା ଏବଂ ଏହାର ସମୟର ସବୁଠାରୁ ଲୋକପ୍ରିୟ ଥିଲା | ୧ 43 1543 ମସିହାରେ ଲଣ୍ଡନରେ ଗ୍ରାଉଣ୍ଡ୍ ଅଫ୍ ଆର୍ଟସ୍ ଦେଖାଦେଲା ଏବଂ ୧ 00 17 ୦ ପର୍ଯ୍ୟନ୍ତ ଏହା ପ୍ରାୟ 45 ଟି ସଂସ୍କରଣରେ ପୁନ int ମୁଦ୍ରିତ ହୋଇଥିଲା।
ଆରିଥମେଟିକୋ - ଜ୍ୟାମିତିକ କ୍ରମ: ଗଣିତରେ, ଏକ ଗାଣିତିକ ପ୍ରଗତିର ଅନୁରୂପ ସର୍ତ୍ତାବଳୀ ସହିତ ଏକ ଜ୍ୟାମିତିକ ପ୍ରଗତିର ଶବ୍ଦ- ଦ୍ -ାରା ଗୁଣନର ଫଳାଫଳ ହେଉଛି ଏକ ଗଣିତ - ଜ୍ୟାମିତିକ କ୍ରମ | ଅଧିକ ସ୍ପଷ୍ଟରୂେପ ରଖ, ଏକ arithmetico-Geometric ସିକ୍ୟୁଏନ୍ସ n ନେଟୱାର୍କରେ ସର୍ତ୍ତାବଳୀକୁ ଉତ୍ପାଦ n ଗୋଟିଏ ଗାଣିତିକ sequenceand n ଏକ Geometric ଏକ ର th ସର୍ତ୍ତାବଳୀକୁ th ଶବ୍ଦ ଅଟେ। ଆରିଥମେଟିକୋ - ଜ୍ୟାମିତିକ କ୍ରମ ବିଭିନ୍ନ ପ୍ରୟୋଗରେ ସୃଷ୍ଟି ହୁଏ, ଯେପରିକି ସମ୍ଭାବ୍ୟତା ସିଦ୍ଧାନ୍ତରେ ଆଶା କରାଯାଉଥିବା ମୂଲ୍ୟର ଗଣନା | ଉଦାହରଣ ସ୍ୱରୂପ, କ୍ରମ |
ଆରିଥମେଟିକୋ - ଜ୍ୟାମିତିକ କ୍ରମ: ଗଣିତରେ, ଏକ ଗାଣିତିକ ପ୍ରଗତିର ଅନୁରୂପ ସର୍ତ୍ତାବଳୀ ସହିତ ଏକ ଜ୍ୟାମିତିକ ପ୍ରଗତିର ଶବ୍ଦ- ଦ୍ -ାରା ଗୁଣନର ଫଳାଫଳ ହେଉଛି ଏକ ଗଣିତ - ଜ୍ୟାମିତିକ କ୍ରମ | ଅଧିକ ସ୍ପଷ୍ଟରୂେପ ରଖ, ଏକ arithmetico-Geometric ସିକ୍ୟୁଏନ୍ସ n ନେଟୱାର୍କରେ ସର୍ତ୍ତାବଳୀକୁ ଉତ୍ପାଦ n ଗୋଟିଏ ଗାଣିତିକ sequenceand n ଏକ Geometric ଏକ ର th ସର୍ତ୍ତାବଳୀକୁ th ଶବ୍ଦ ଅଟେ। ଆରିଥମେଟିକୋ - ଜ୍ୟାମିତିକ କ୍ରମ ବିଭିନ୍ନ ପ୍ରୟୋଗରେ ସୃଷ୍ଟି ହୁଏ, ଯେପରିକି ସମ୍ଭାବ୍ୟତା ସିଦ୍ଧାନ୍ତରେ ଆଶା କରାଯାଉଥିବା ମୂଲ୍ୟର ଗଣନା | ଉଦାହରଣ ସ୍ୱରୂପ, କ୍ରମ |
ଆରିଥମେଟିକୋ - ଜ୍ୟାମିତିକ କ୍ରମ: ଗଣିତରେ, ଏକ ଗାଣିତିକ ପ୍ରଗତିର ଅନୁରୂପ ସର୍ତ୍ତାବଳୀ ସହିତ ଏକ ଜ୍ୟାମିତିକ ପ୍ରଗତିର ଶବ୍ଦ- ଦ୍ -ାରା ଗୁଣନର ଫଳାଫଳ ହେଉଛି ଏକ ଗଣିତ - ଜ୍ୟାମିତିକ କ୍ରମ | ଅଧିକ ସ୍ପଷ୍ଟରୂେପ ରଖ, ଏକ arithmetico-Geometric ସିକ୍ୟୁଏନ୍ସ n ନେଟୱାର୍କରେ ସର୍ତ୍ତାବଳୀକୁ ଉତ୍ପାଦ n ଗୋଟିଏ ଗାଣିତିକ sequenceand n ଏକ Geometric ଏକ ର th ସର୍ତ୍ତାବଳୀକୁ th ଶବ୍ଦ ଅଟେ। ଆରିଥମେଟିକୋ - ଜ୍ୟାମିତିକ କ୍ରମ ବିଭିନ୍ନ ପ୍ରୟୋଗରେ ସୃଷ୍ଟି ହୁଏ, ଯେପରିକି ସମ୍ଭାବ୍ୟତା ସିଦ୍ଧାନ୍ତରେ ଆଶା କରାଯାଉଥିବା ମୂଲ୍ୟର ଗଣନା | ଉଦାହରଣ ସ୍ୱରୂପ, କ୍ରମ |
ଆରିଥମେଟିକୋ - ଜ୍ୟାମିତିକ କ୍ରମ: ଗଣିତରେ, ଏକ ଗାଣିତିକ ପ୍ରଗତିର ଅନୁରୂପ ସର୍ତ୍ତାବଳୀ ସହିତ ଏକ ଜ୍ୟାମିତିକ ପ୍ରଗତିର ଶବ୍ଦ- ଦ୍ -ାରା ଗୁଣନର ଫଳାଫଳ ହେଉଛି ଏକ ଗଣିତ - ଜ୍ୟାମିତିକ କ୍ରମ | ଅଧିକ ସ୍ପଷ୍ଟରୂେପ ରଖ, ଏକ arithmetico-Geometric ସିକ୍ୟୁଏନ୍ସ n ନେଟୱାର୍କରେ ସର୍ତ୍ତାବଳୀକୁ ଉତ୍ପାଦ n ଗୋଟିଏ ଗାଣିତିକ sequenceand n ଏକ Geometric ଏକ ର th ସର୍ତ୍ତାବଳୀକୁ th ଶବ୍ଦ ଅଟେ। ଆରିଥମେଟିକୋ - ଜ୍ୟାମିତିକ କ୍ରମ ବିଭିନ୍ନ ପ୍ରୟୋଗରେ ସୃଷ୍ଟି ହୁଏ, ଯେପରିକି ସମ୍ଭାବ୍ୟତା ସିଦ୍ଧାନ୍ତରେ ଆଶା କରାଯାଉଥିବା ମୂଲ୍ୟର ଗଣନା | ଉଦାହରଣ ସ୍ୱରୂପ, କ୍ରମ |
ଆରିଥମେଟିକୋ - ଜ୍ୟାମିତିକ କ୍ରମ: ଗଣିତରେ, ଏକ ଗାଣିତିକ ପ୍ରଗତିର ଅନୁରୂପ ସର୍ତ୍ତାବଳୀ ସହିତ ଏକ ଜ୍ୟାମିତିକ ପ୍ରଗତିର ଶବ୍ଦ- ଦ୍ -ାରା ଗୁଣନର ଫଳାଫଳ ହେଉଛି ଏକ ଗଣିତ - ଜ୍ୟାମିତିକ କ୍ରମ | ଅଧିକ ସ୍ପଷ୍ଟରୂେପ ରଖ, ଏକ arithmetico-Geometric ସିକ୍ୟୁଏନ୍ସ n ନେଟୱାର୍କରେ ସର୍ତ୍ତାବଳୀକୁ ଉତ୍ପାଦ n ଗୋଟିଏ ଗାଣିତିକ sequenceand n ଏକ Geometric ଏକ ର th ସର୍ତ୍ତାବଳୀକୁ th ଶବ୍ଦ ଅଟେ। ଆରିଥମେଟିକୋ - ଜ୍ୟାମିତିକ କ୍ରମ ବିଭିନ୍ନ ପ୍ରୟୋଗରେ ସୃଷ୍ଟି ହୁଏ, ଯେପରିକି ସମ୍ଭାବ୍ୟତା ସିଦ୍ଧାନ୍ତରେ ଆଶା କରାଯାଉଥିବା ମୂଲ୍ୟର ଗଣନା | ଉଦାହରଣ ସ୍ୱରୂପ, କ୍ରମ |
ଆରିଥମେଟିକୋ - ଜ୍ୟାମିତିକ କ୍ରମ: ଗଣିତରେ, ଏକ ଗାଣିତିକ ପ୍ରଗତିର ଅନୁରୂପ ସର୍ତ୍ତାବଳୀ ସହିତ ଏକ ଜ୍ୟାମିତିକ ପ୍ରଗତିର ଶବ୍ଦ- ଦ୍ -ାରା ଗୁଣନର ଫଳାଫଳ ହେଉଛି ଏକ ଗଣିତ - ଜ୍ୟାମିତିକ କ୍ରମ | ଅଧିକ ସ୍ପଷ୍ଟରୂେପ ରଖ, ଏକ arithmetico-Geometric ସିକ୍ୟୁଏନ୍ସ n ନେଟୱାର୍କରେ ସର୍ତ୍ତାବଳୀକୁ ଉତ୍ପାଦ n ଗୋଟିଏ ଗାଣିତିକ sequenceand n ଏକ Geometric ଏକ ର th ସର୍ତ୍ତାବଳୀକୁ th ଶବ୍ଦ ଅଟେ। ଆରିଥମେଟିକୋ - ଜ୍ୟାମିତିକ କ୍ରମ ବିଭିନ୍ନ ପ୍ରୟୋଗରେ ସୃଷ୍ଟି ହୁଏ, ଯେପରିକି ସମ୍ଭାବ୍ୟତା ସିଦ୍ଧାନ୍ତରେ ଆଶା କରାଯାଉଥିବା ମୂଲ୍ୟର ଗଣନା | ଉଦାହରଣ ସ୍ୱରୂପ, କ୍ରମ |
ଗାଣିତିକ: ଆରିଥମେଟିକ୍ ହେଉଛି ଗଣିତର ଏକ ଶାଖା ଯାହା ସଂଖ୍ୟାଗୁଡ଼ିକର ଅଧ୍ୟୟନକୁ ନେଇ ଗଠିତ, ବିଶେଷତ them ସେମାନଙ୍କ ଉପରେ ପାରମ୍ପାରିକ କାର୍ଯ୍ୟର ଗୁଣ - ଯୋଗ, ବିତରଣ, ଗୁଣନ, ବିଭାଜନ, ମୂଳ ଏବଂ ନିର୍ବାହ | ଆରିଥମେଟିକ୍ ହେଉଛି ସଂଖ୍ୟା ତତ୍ତ୍ an ର ଏକ ପ୍ରାଥମିକ ଅଂଶ, ଏବଂ ସଂଖ୍ୟା ଥିଓରୀକୁ ଆଧୁନିକ ଗଣିତର ଏକ ଉଚ୍ଚ ସ୍ତରୀୟ ବିଭାଗ ଭାବରେ ବିବେଚନା କରାଯାଏ, ବୀଜ୍, ଜ୍ୟାମିତି ଏବଂ ବିଶ୍ଳେଷଣ ସହିତ | ଆରିଥମେଟିକ୍ ଏବଂ ଉଚ୍ଚ ଆରିଥମେଟିକ୍ ଶବ୍ଦଗୁଡିକ ବିଂଶ ଶତାବ୍ଦୀର ଆରମ୍ଭ ପର୍ଯ୍ୟନ୍ତ ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତର ସମକକ୍ଷ ଭାବରେ ବ୍ୟବହୃତ ହୋଇଥିଲା ଏବଂ ବେଳେବେଳେ ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତର ଏକ ବ୍ୟାପକ ଅଂଶକୁ ସୂଚାଇବା ପାଇଁ ବ୍ୟବହୃତ ହୁଏ |
ଗାଣିତିକ - ଜ୍ୟାମିତିକ ଅର୍ଥ: ଗଣିତରେ, ଦୁଇଟି ସକାରାତ୍ମକ ପ୍ରକୃତ ସଂଖ୍ୟା x ଏବଂ y ର ଗାଣିତିକ - ଜ୍ୟାମିତିକ ଅର୍ଥ ( AGM ) କୁ ନିମ୍ନଲିଖିତ ଭାବରେ ବ୍ୟାଖ୍ୟା କରାଯାଇଛି:
ଗାଣିତିକ ଏବଂ ଜ୍ୟାମିତିକ ଅର୍ଥର ଅସମାନତା: ଗଣିତରେ, ଗାଣିତିକ ଏବଂ ଜ୍ୟାମିତିକ ଅର୍ଥର ଅସମାନତା , କିମ୍ବା ଅଧିକ ସଂକ୍ଷେପରେ AM - GM ଅସମାନତା ଦର୍ଶାଏ ଯେ ଅଣ-ନକାରାତ୍ମକ ପ୍ରକୃତ ସଂଖ୍ୟାର ତାଲିକାର ଗାଣିତିକ ଅର୍ଥ ସମାନ ତାଲିକାର ଜ୍ୟାମିତିକ ଅର୍ଥଠାରୁ ଅଧିକ କିମ୍ବା ସମାନ; ଏବଂ ଆହୁରି ମଧ୍ୟ, ଯଦି ତାଲିକାର ପ୍ରତ୍ୟେକ ସଂଖ୍ୟା ସମାନ ତେବେ ଦୁଇଟି ଅର୍ଥ ସମାନ |
ଜ୍ୟାମିତିକ ଅର୍ଥ: ଗଣିତରେ, ଜ୍ୟାମିତିକ ଅର୍ଥ ହେଉଛି ଏକ ହାରାହାରି ବା ହାରାହାରି, ଯାହା ସେମାନଙ୍କର ମୂଲ୍ୟର ଉତ୍ପାଦ ବ୍ୟବହାର କରି ସଂଖ୍ୟାଗୁଡ଼ିକର ଏକ ସେଟ୍ ର କେନ୍ଦ୍ରୀୟ ପ୍ରବୃତ୍ତି କିମ୍ବା ସାଧାରଣ ମୂଲ୍ୟକୁ ସୂଚିତ କରେ | ଜ୍ୟାମିତିକ ଅର୍ଥ n ସଂଖ୍ୟାର ଉତ୍ପାଦର n th ମୂଳ ଭାବରେ ବ୍ୟାଖ୍ୟା କରାଯାଇଛି, ଅର୍ଥାତ୍ x 1 , x 2 , ..., x n ସଂଖ୍ୟାଗୁଡ଼ିକର ଏକ ସେଟ୍ ପାଇଁ, ଜ୍ୟାମିତିକ ଅର୍ଥ ପରି ବ୍ୟାଖ୍ୟା କରାଯାଇଛି |
ଗାଣିତିକ ତର୍କ ଏକକ: ଗଣନାରେ, ଏକ ଆରିଥମେଟିକ୍ ଲଜିକ୍ ୟୁନିଟ୍ (ALU) ହେଉଛି ଏକ ମିଳିତ ଡିଜିଟାଲ୍ ସର୍କିଟ୍ ଯାହା ଇଣ୍ଟିଜର୍ ବାଇନାରୀ ନମ୍ବର ଉପରେ ଗାଣିତିକ ଏବଂ ବିଟୱାଇସ୍ ଅପରେସନ୍ କରିଥାଏ | ଏହା ଏକ ଫ୍ଲୋଟିଂ ପଏଣ୍ଟ ୟୁନିଟ୍ (FPU) ର ବିପରୀତ, ଯାହା ଫ୍ଲୋଟିଂ ପଏଣ୍ଟ ନମ୍ବର ଉପରେ କାର୍ଯ୍ୟ କରେ | ଏହା କମ୍ପ୍ୟୁଟର, FPU ଏବଂ ଗ୍ରାଫିକ୍ସ ପ୍ରକ୍ରିୟାକରଣ ୟୁନିଟ୍ (ଜିପିୟୁ) ର କେନ୍ଦ୍ରୀୟ ପ୍ରକ୍ରିୟାକରଣ ୟୁନିଟ୍ (CPU) ଅନ୍ତର୍ଭୂକ୍ତ କରି ଅନେକ ପ୍ରକାରର ଗଣନା ସର୍କିଟ୍ ର ଏକ ମ fundamental ଳିକ ବିଲ୍ଡିଂ ବ୍ଲକ୍ |
ଗାଣିତିକ: ଆରିଥମେଟିକ୍ ହେଉଛି ଗଣିତର ଏକ ଶାଖା ଯାହା ସଂଖ୍ୟାଗୁଡ଼ିକର ଅଧ୍ୟୟନକୁ ନେଇ ଗଠିତ, ବିଶେଷତ them ସେମାନଙ୍କ ଉପରେ ପାରମ୍ପାରିକ କାର୍ଯ୍ୟର ଗୁଣ - ଯୋଗ, ବିତରଣ, ଗୁଣନ, ବିଭାଜନ, ମୂଳ ଏବଂ ନିର୍ବାହ | ଆରିଥମେଟିକ୍ ହେଉଛି ସଂଖ୍ୟା ତତ୍ତ୍ an ର ଏକ ପ୍ରାଥମିକ ଅଂଶ, ଏବଂ ସଂଖ୍ୟା ଥିଓରୀକୁ ଆଧୁନିକ ଗଣିତର ଏକ ଉଚ୍ଚ ସ୍ତରୀୟ ବିଭାଗ ଭାବରେ ବିବେଚନା କରାଯାଏ, ବୀଜ୍, ଜ୍ୟାମିତି ଏବଂ ବିଶ୍ଳେଷଣ ସହିତ | ଆରିଥମେଟିକ୍ ଏବଂ ଉଚ୍ଚ ଆରିଥମେଟିକ୍ ଶବ୍ଦଗୁଡିକ ବିଂଶ ଶତାବ୍ଦୀର ଆରମ୍ଭ ପର୍ଯ୍ୟନ୍ତ ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତର ସମକକ୍ଷ ଭାବରେ ବ୍ୟବହୃତ ହୋଇଥିଲା ଏବଂ ବେଳେବେଳେ ସଂଖ୍ୟା ସିଦ୍ଧାନ୍ତର ଏକ ବ୍ୟାପକ ଅଂଶକୁ ସୂଚାଇବା ପାଇଁ ବ୍ୟବହୃତ ହୁଏ |
ବିଶ୍ଳେଷଣର ଗଣିତ: ବିଶ୍ଳେଷଣର ଆରିଥମେଟାଇଜେସନ୍ 19th ନବିଂଶ ଶତାବ୍ଦୀର ଦ୍ୱିତୀୟାର୍ଦ୍ଧରେ ଗଣିତର ମୂଳଦୁଆରେ ଏକ ଅନୁସନ୍ଧାନ କାର୍ଯ୍ୟକ୍ରମ ଥିଲା |
ବିଶ୍ଳେଷଣର ଗଣିତ: ବିଶ୍ଳେଷଣର ଆରିଥମେଟାଇଜେସନ୍ 19th ନବିଂଶ ଶତାବ୍ଦୀର ଦ୍ୱିତୀୟାର୍ଦ୍ଧରେ ଗଣିତର ମୂଳଦୁଆରେ ଏକ ଅନୁସନ୍ଧାନ କାର୍ଯ୍ୟକ୍ରମ ଥିଲା |
ବିଶ୍ଳେଷଣର ଗଣିତ: ବିଶ୍ଳେଷଣର ଆରିଥମେଟାଇଜେସନ୍ 19th ନବିଂଶ ଶତାବ୍ଦୀର ଦ୍ୱିତୀୟାର୍ଦ୍ଧରେ ଗଣିତର ମୂଳଦୁଆରେ ଏକ ଅନୁସନ୍ଧାନ କାର୍ଯ୍ୟକ୍ରମ ଥିଲା |
ଗୋଡେଲଙ୍କ ଅସମ୍ପୂର୍ଣ୍ଣତା ଥିଓରେମ୍: ଗୋଡେଲଙ୍କ ଅସମ୍ପୂର୍ଣ୍ଣତା ଥିଓରେମଗୁଡିକ ହେଉଛି ଗାଣିତିକ ତର୍କର ଦୁଇଟି ତତ୍ତ୍ that ଯାହା ଆନୁଷ୍ଠାନିକ ସ୍ୱୀକୃତି ତତ୍ତ୍ prov ରେ ପ୍ରୋଭିବିଲିଟିର ସୀମା ସହିତ ଜଡିତ | 1931 ମସିହାରେ କୁର୍ଟ ଗୋଡେଲଙ୍କ ଦ୍ published ାରା ପ୍ରକାଶିତ ଏହି ଫଳାଫଳଗୁଡିକ ଉଭୟ ଗାଣିତିକ ତର୍କ ଏବଂ ଗଣିତ ଦର୍ଶନରେ ଗୁରୁତ୍ୱପୂର୍ଣ୍ଣ | ଥିଓରେମଗୁଡିକ ବ୍ୟାପକ, କିନ୍ତୁ ସର୍ବଭାରତୀୟ ସ୍ତରରେ ନୁହେଁ, ବ୍ୟାଖ୍ୟା କରାଯାଇଛି ଯେ ସମସ୍ତ ଗଣିତ ପାଇଁ ଏକ ସମ୍ପୂର୍ଣ୍ଣ ଏବଂ ସ୍ଥିର ଆକ୍ସିୟୋମ୍ ସେଟ୍ ଖୋଜିବା ପାଇଁ ହିଲବର୍ଟଙ୍କ କାର୍ଯ୍ୟକ୍ରମ ଅସମ୍ଭବ ଅଟେ |
ଆରିଥମିୟମ୍: ଆରିଥମିୟମ୍ ହେଉଛି ଏକ ଗଣିତ ସଂଗ୍ରହାଳୟ ଯାହା ବୋନ୍ ବିଶ୍ୱବିଦ୍ୟାଳୟରେ ଫୋର୍ସୁଙ୍ଗସିନଷ୍ଟିଟଟ୍ ଫୁର୍ ଡିସ୍କ୍ରେଟ୍ ଗଣିତ |
ଆରିଥମୋଲୋଜି: ଆରିଥମୋଲୋଜି, ସାଇଭ୍ ଡି ଅବଡିଟିସ୍ ନ୍ୟୁମେରମ୍ ମିଷ୍ଟେରିସ୍ ହେଉଛି ଜେସୁଟ୍ ପଣ୍ଡିତ ଆଥାନାସିୟସ୍ କିର୍ଚର୍ ଙ୍କ 1665 କାର୍ଯ୍ୟ | 17 ଶତାବ୍ଦୀର ମଧ୍ୟଭାଗରେ ରୋମରେ ଥିବା ଜେସୁଟ୍ ଅର୍ଡର ପାଇଁ ମୁଖ୍ୟ ପ୍ରିଣ୍ଟିଂ ହାଉସ୍ ଭାରେସ୍ ଦ୍ୱାରା ଏହା ପ୍ରକାଶିତ ହୋଇଥିଲା | ଏହା ଫ୍ରାଞ୍ଜ ତୃତୀୟ ପାଇଁ ଉତ୍ସର୍ଗୀକୃତ ହୋଇଥିଲା | ନାଡାସ୍ଡି, କ୍ୟାଥୋଲିକ୍ ଧର୍ମ ଗ୍ରହଣ କରିଥିବା ବ୍ୟକ୍ତିଙ୍କ ସହ କିର୍ଚର୍ ପୂର୍ବରୁ ଓଡିପସ୍ ଏଜିପ୍ଟିଆକସ୍ ସହ-ଉତ୍ସର୍ଗ କରିଥିଲେ। ଆରିଥମୋଲୋଜି ହେଉଛି କିର୍ଚରଙ୍କ ଏକମାତ୍ର କାର୍ଯ୍ୟ ଯାହାକି ସଂପୂର୍ଣ୍ଣ ଭାବରେ ସଂଖ୍ୟା ପ୍ରତୀକର ବିଭିନ୍ନ ଦିଗ ପ୍ରତି ଉତ୍ସର୍ଗୀକୃତ |
ସଂଖ୍ୟାସଂଖ୍ୟା: ସଂଖ୍ୟା ଏବଂ ଏକ କିମ୍ବା ଏକାଧିକ ସମକକ୍ଷ ଘଟଣା ମଧ୍ୟରେ divine ଶ୍ୱରୀୟ କିମ୍ବା ରହସ୍ୟମୟ ସମ୍ପର୍କ ଉପରେ ନମ୍ବରୋଲୋଜି ହେଉଛି ବିଶ୍ୱାସ | ଏହା ମଧ୍ୟ ଶବ୍ଦ, ନାମ ଏବଂ ଚିନ୍ତାଧାରାରେ ଅକ୍ଷରର ସାଂଖ୍ୟିକ ମୂଲ୍ୟର ଅଧ୍ୟୟନ | ଏହା ପ୍ରାୟତ the ଜ୍ୟୋତିଷ ଶାସ୍ତ୍ର ସହିତ ପରମାନନ୍ଦ ସହିତ ଜଡିତ ଏବଂ ବିଭାଜିତ କଳା ସହିତ ସମାନ |
ରିଥମୋମାଚି: ରିଥୋମାଚି ଏକ ଅତ୍ୟନ୍ତ ଜଟିଳ, ପ୍ରାରମ୍ଭିକ ୟୁରୋପୀୟ ଗାଣିତିକ ବୋର୍ଡ ଖେଳ | ଏହାର ସର୍ବପ୍ରଥମ ଜଣାଶୁଣା ବର୍ଣ୍ଣନା ଏକାଦଶ ଶତାବ୍ଦୀରୁ ଆରମ୍ଭ ହୋଇଥିଲା | ନାମର ଏକ ଆକ୍ଷରିକ ଅନୁବାଦ ହେଉଛି "ସଂଖ୍ୟାଗୁଡିକର ଯୁଦ୍ଧ" | ଖେଳଟି ଚେସ ପରି, କ୍ୟାପଚରର ଅଧିକାଂଶ ପଦ୍ଧତି ପ୍ରତ୍ୟେକ ଖଣ୍ଡରେ ଲେଖାଯାଇଥିବା ସଂଖ୍ୟା ଉପରେ ନିର୍ଭର କରେ |
ଆରିଥମ୍ୟାନ୍ସି: ଆଧୁନିକ ସାଂଖ୍ୟିକ ଶବ୍ଦଗୁଡ଼ିକରେ, ଗାଣିତିକତା ହେଉଛି ଏକ ଶବ୍ଦ ବା ବାକ୍ୟାଂଶରେ ସାଂଖ୍ୟିକ ମୂଲ୍ୟ ନ୍ୟସ୍ତ କରିବା ଉପରେ ଆଧାର କରି ପ୍ରାଚୀନ ଗ୍ରୀକ୍ ଆଇସୋସେଫି କିମ୍ବା ହିବ୍ରୁ / ଆରାମିକ୍ ଜେମାଟ୍ରିଆର ସରଳୀକୃତ ସଂସ୍କରଣ ମାଧ୍ୟମରେ, ଲାଟିନ୍ ବର୍ଣ୍ଣମାଳା ସହିତ ଅନୁକୂଳ | ଆରିଥମ୍ୟାନ୍ସି କଲଦୀୟ, ପ୍ଲାଟୋନିଷ୍ଟ, ପାଇଥାଗୋରୀୟ ଏବଂ କବାବାଲା ସହିତ ଜଡିତ | ଯେତେବେଳେ ଜଣେ ବ୍ୟକ୍ତିଙ୍କ ନାମରେ ଗଣିତ ପ୍ରୟୋଗ କରାଯାଏ, ଏହା ଏକ ଅନୋମ୍ୟାନ୍ସିର ଏକ ରୂପ |
ଆରିଥମୋମାନିଆ: ଆରିଥମୋମାନିଆ ହେଉଛି ଏକ ମାନସିକ ବିକୃତି ଯାହା ଅବସେସିଭ୍ - ବାଧ୍ୟତାମୂଳକ ବ୍ୟାଧି (OCD) ର ଅଭିବ୍ୟକ୍ତି ଭାବରେ ଦେଖାଯାଇପାରେ | ଏହି ବ୍ୟାଧିରେ ପୀଡିତ ବ୍ୟକ୍ତିବିଶେଷଙ୍କର ନିଜ କାର୍ଯ୍ୟ କିମ୍ବା ବସ୍ତୁକୁ ନିଜ ଆଖପାଖରେ ଗଣନା କରିବାର ପ୍ରବଳ ଆବଶ୍ୟକତା ଅଛି |
ଆରିଥମୋମାନିଆ: ଆରିଥମୋମାନିଆ ହେଉଛି ଏକ ମାନସିକ ବିକୃତି ଯାହା ଅବସେସିଭ୍ - ବାଧ୍ୟତାମୂଳକ ବ୍ୟାଧି (OCD) ର ଅଭିବ୍ୟକ୍ତି ଭାବରେ ଦେଖାଯାଇପାରେ | ଏହି ବ୍ୟାଧିରେ ପୀଡିତ ବ୍ୟକ୍ତିବିଶେଷଙ୍କର ନିଜ କାର୍ଯ୍ୟ କିମ୍ବା ବସ୍ତୁକୁ ନିଜ ଆଖପାଖରେ ଗଣନା କରିବାର ପ୍ରବଳ ଆବଶ୍ୟକତା ଅଛି |
ଆରିଥମୋମିଟର: ଆରିଥମୋମିଟର ବା ଆରିଥମୋମେଟ୍ରେ ପ୍ରଥମ ଡିଜିଟାଲ୍ ଯାନ୍ତ୍ରିକ କାଲକୁଲେଟର ଯଥେଷ୍ଟ ଶକ୍ତିଶାଳୀ ଏବଂ ଏକ ଅଫିସ୍ ପରିବେଶରେ ପ୍ରତିଦିନ ବ୍ୟବହୃତ ହେବା ପାଇଁ ଯଥେଷ୍ଟ ନିର୍ଭରଯୋଗ୍ୟ | ଏହି କାଲକୁଲେଟର ସିଧାସଳଖ ଦୁଇଟି ସଂଖ୍ୟା ଯୋଡି ଏବଂ ବିଛିନ୍ନ କରିପାରେ ଏବଂ ଫଳାଫଳ ପାଇଁ ଏକ ଚଳନକାରୀ ଜମାକାରୀ ବ୍ୟବହାର କରି ଲମ୍ବା ଗୁଣନ ଏବଂ ବିଭାଜନକୁ ପ୍ରଭାବଶାଳୀ ଭାବରେ କାର୍ଯ୍ୟ କରିପାରିବ |
ଆରିଥମୋମିଟର: ଆରିଥମୋମିଟର ବା ଆରିଥମୋମେଟ୍ରେ ପ୍ରଥମ ଡିଜିଟାଲ୍ ଯାନ୍ତ୍ରିକ କାଲକୁଲେଟର ଯଥେଷ୍ଟ ଶକ୍ତିଶାଳୀ ଏବଂ ଏକ ଅଫିସ୍ ପରିବେଶରେ ପ୍ରତିଦିନ ବ୍ୟବହୃତ ହେବା ପାଇଁ ଯଥେଷ୍ଟ ନିର୍ଭରଯୋଗ୍ୟ | ଏହି କାଲକୁଲେଟର ସିଧାସଳଖ ଦୁଇଟି ସଂଖ୍ୟା ଯୋଡି ଏବଂ ବିଛିନ୍ନ କରିପାରେ ଏବଂ ଫଳାଫଳ ପାଇଁ ଏକ ଚଳନକାରୀ ଜମାକାରୀ ବ୍ୟବହାର କରି ଲମ୍ବା ଗୁଣନ ଏବଂ ବିଭାଜନକୁ ପ୍ରଭାବଶାଳୀ ଭାବରେ କାର୍ଯ୍ୟ କରିପାରିବ |
ଆରିଥମୋମିଟର: ଆରିଥମୋମିଟର ବା ଆରିଥମୋମେଟ୍ରେ ପ୍ରଥମ ଡିଜିଟାଲ୍ ଯାନ୍ତ୍ରିକ କାଲକୁଲେଟର ଯଥେଷ୍ଟ ଶକ୍ତିଶାଳୀ ଏବଂ ଏକ ଅଫିସ୍ ପରିବେଶରେ ପ୍ରତିଦିନ ବ୍ୟବହୃତ ହେବା ପାଇଁ ଯଥେଷ୍ଟ ନିର୍ଭରଯୋଗ୍ୟ | ଏହି କାଲକୁଲେଟର ସିଧାସଳଖ ଦୁଇଟି ସଂଖ୍ୟା ଯୋଡି ଏବଂ ବିଛିନ୍ନ କରିପାରେ ଏବଂ ଫଳାଫଳ ପାଇଁ ଏକ ଚଳନକାରୀ ଜମାକାରୀ ବ୍ୟବହାର କରି ଲମ୍ବା ଗୁଣନ ଏବଂ ବିଭାଜନକୁ ପ୍ରଭାବଶାଳୀ ଭାବରେ କାର୍ଯ୍ୟ କରିପାରିବ |
ଆରିଥମ୍ୟାନ୍ସି: ଆଧୁନିକ ସାଂଖ୍ୟିକ ଶବ୍ଦଗୁଡ଼ିକରେ, ଗାଣିତିକତା ହେଉଛି ଏକ ଶବ୍ଦ ବା ବାକ୍ୟାଂଶରେ ସାଂଖ୍ୟିକ ମୂଲ୍ୟ ନ୍ୟସ୍ତ କରିବା ଉପରେ ଆଧାର କରି ପ୍ରାଚୀନ ଗ୍ରୀକ୍ ଆଇସୋସେଫି କିମ୍ବା ହିବ୍ରୁ / ଆରାମିକ୍ ଜେମାଟ୍ରିଆର ସରଳୀକୃତ ସଂସ୍କରଣ ମାଧ୍ୟମରେ, ଲାଟିନ୍ ବର୍ଣ୍ଣମାଳା ସହିତ ଅନୁକୂଳ | ଆରିଥମ୍ୟାନ୍ସି କଲଦୀୟ, ପ୍ଲାଟୋନିଷ୍ଟ, ପାଇଥାଗୋରୀୟ ଏବଂ କବାବାଲା ସହିତ ଜଡିତ | ଯେତେବେଳେ ଜଣେ ବ୍ୟକ୍ତିଙ୍କ ନାମରେ ଗଣିତ ପ୍ରୟୋଗ କରାଯାଏ, ଏହା ଏକ ଅନୋମ୍ୟାନ୍ସିର ଏକ ରୂପ |
ଆଲୋକ ଏବଂ ଛାୟାର ଯୁଦ୍ଧ: ଲାଇଟ୍ ଆଣ୍ଡ୍ ଛାୟାର ଯୁଦ୍ଧ ହେଉଛି ଜାନି ୱର୍ଟସ୍ ଙ୍କ କଳ୍ପନା ପୁସ୍ତକ | ସମାପ୍ତ ହେବା ପରେ, ଏହା ପାଞ୍ଚଟି କାହାଣୀ ଆର୍କକୁ ନେଇ ଗଠିତ ହେବ, ପ୍ରଥମ ଚାରୋଟି ଆର୍କ ସମ୍ପୂର୍ଣ୍ଣ ହେବ |
ଆଲୋକ ଏବଂ ଛାୟାର ଯୁଦ୍ଧ: ଲାଇଟ୍ ଆଣ୍ଡ୍ ଛାୟାର ଯୁଦ୍ଧ ହେଉଛି ଜାନି ୱର୍ଟସ୍ ଙ୍କ କଳ୍ପନା ପୁସ୍ତକ | ସମାପ୍ତ ହେବା ପରେ, ଏହା ପାଞ୍ଚଟି କାହାଣୀ ଆର୍କକୁ ନେଇ ଗଠିତ ହେବ, ପ୍ରଥମ ଚାରୋଟି ଆର୍କ ସମ୍ପୂର୍ଣ୍ଣ ହେବ |
ଆଲୋକ ଏବଂ ଛାୟାର ଯୁଦ୍ଧ: ଲାଇଟ୍ ଆଣ୍ଡ୍ ଛାୟାର ଯୁଦ୍ଧ ହେଉଛି ଜାନି ୱର୍ଟସ୍ ଙ୍କ କଳ୍ପନା ପୁସ୍ତକ | ସମାପ୍ତ ହେବା ପରେ, ଏହା ପାଞ୍ଚଟି କାହାଣୀ ଆର୍କକୁ ନେଇ ଗଠିତ ହେବ, ପ୍ରଥମ ଚାରୋଟି ଆର୍କ ସମ୍ପୂର୍ଣ୍ଣ ହେବ |
ଟାନା ନଦୀ କାଉଣ୍ଟି: ତାନା ନଦୀ କାଉଣ୍ଟି କେନିଆର ପୂର୍ବ ତଟ ପ୍ରଦେଶର ଏକ କାଉଣ୍ଟି | ଏହାର ନାମ ତାନା ନଦୀ ନାମରେ ରଖାଯାଇଛି | ଏହାର କ୍ଷେତ୍ର 38,437 ବର୍ଗ କିଲୋମିଟର (14,841 ବର୍ଗ ମାଇଲ) ଏବଂ ଜନସଂଖ୍ୟା 315,943 | ରାଜଧାନୀ ଏବଂ ବୃହତ୍ତମ ସହର ହେଉଛି ହୋଲା |
ଆରିଟି: ଯୁକ୍ତି, ଗଣିତ ଏବଂ କମ୍ପ୍ୟୁଟର ବିଜ୍ଞାନରେ ଏକ କାର୍ଯ୍ୟ କିମ୍ବା କାର୍ଯ୍ୟ ଦ୍ୱାରା ନିଆଯାଇଥିବା ଆର୍ଗୁମେଣ୍ଟ୍ ବା ଅପରେଣ୍ଡ୍ ସଂଖ୍ୟା | ଗଣିତରେ, ଆରିଟିକୁ ମଧ୍ୟ ରାଙ୍କ୍ କୁହାଯାଇପାରେ, କିନ୍ତୁ ଏହି ଶବ୍ଦର ଗଣିତରେ ଅନ୍ୟାନ୍ୟ ଅନେକ ଅର୍ଥ ଥାଇପାରେ | ତର୍କ ଏବଂ ଦର୍ଶନରେ ଏହାକୁ ଆଡିସିଟି ଏବଂ ଡିଗ୍ରୀ ମଧ୍ୟ କୁହାଯାଏ | ଭାଷା ବିଜ୍ଞାନରେ ଏହାକୁ ସାଧାରଣତ val ଭାଲେନ୍ସି କୁହାଯାଏ |
କୃତ୍ରିମ ସ୍ନାୟୁ ନେଟୱାର୍କ: କୃତ୍ରିମ ସ୍ନାୟୁ ନେଟୱାର୍କ ( ANNs ), ସାଧାରଣତ simply କେବଳ ନ୍ୟୁରାଲ୍ ନେଟୱାର୍କ ( NNs ) କୁହାଯାଏ, ଗଣନା ପ୍ରଣାଳୀଗୁଡିକ ଜ bi ବିକ ସ୍ନାୟୁ ନେଟୱାର୍କ ଦ୍ୱାରା ଅସ୍ପଷ୍ଟ ଭାବରେ ଅନୁପ୍ରାଣିତ ହୋଇଥାଏ ଯାହା ପଶୁ ମସ୍ତିଷ୍କ ଗଠନ କରିଥାଏ |
ଆର୍ଟେମିସ୍: ଆର୍ଟେମିସ୍ ହେଉଛି ଶିକାରର ଗ୍ରୀକ୍ ଦେବୀ, ମରୁଭୂମି, ବଣୁଆ ଜନ୍ତୁ, ଚନ୍ଦ୍ର ଏବଂ ସଠିକତା | ଦେବୀ ଡାଏନା ତାଙ୍କର ରୋମାନ୍ ସମକକ୍ଷ |
ଆରିଣ୍ଟିକା: ଆଲିଣ୍ଟିକା ହେଉଛି ଚିଲିର ଆରିକା ୟ ପାରିନାକୋଟା ଅଞ୍ଚଳରେ, ବଲିଭିଆର ସୀମା ନିକଟରେ ଅବସ୍ଥିତ ଏକ ଷ୍ଟ୍ରାଟୋଭୋଲକାନୋ | ଏହା ସାଲାର ଡି ସୁରେରିଆର ଉତ୍ତରରେ ଅବସ୍ଥିତ | ଏହି ଆଗ୍ନେୟଗିରିର ଉତ୍ତରରେ ଏକ ମୁଖ୍ୟ ଶିଖର ସମ୍ମିଳନୀ, ଟିକିଏ ଛୋଟ ଦକ୍ଷିଣ ଶିଖର ଏବଂ ପଶ୍ଚିମରେ ଏକ ସହାୟକ ଶିଖର | ଶିଖର ମଧ୍ୟରେ ଏକ ଗ୍ଲେସିୟର ଉପତ୍ୟକା ଅବସ୍ଥିତ | ତୁଷାରପାତର ଉଚ୍ଚତା 5,590 ମିଟର (18,340 ଫୁଟ) | ଆରିଣ୍ଟିକାରେ ମିଳୁଥିବା ଦ୍ୱିତୀୟ ପର୍ଯ୍ୟାୟ ମୋରେନଗୁଡିକର ଉଚ୍ଚତା 4,350 ମିଟର (14,270 ଫୁଟ) ଠାରୁ ଦକ୍ଷିଣ ପାଶ୍ୱର୍ରେ 4,550 ମିଟର (14,930 ଫୁଟ) ପର୍ଯ୍ୟନ୍ତ ରହିଛି | ପଶ୍ଚିମ ପାର୍ଶ୍ୱରେ ସେମାନେ 4,400 ମିଟର (14,400 ଫୁଟ) ଉଚ୍ଚତାରେ ପହଞ୍ଚନ୍ତି | ମୋଟ ଉପରେ, ପାଞ୍ଚଟି ଗ୍ଲେସିର୍ ଆରିଣ୍ଟିକାକୁ ଘେରି ରହି ସାଲାର୍ ଡି ସୁରେରେ ନିଷ୍କାସିତ ହୋଇଥିଲେ | ବର୍ତ୍ତମାନ, ପର୍ବତ ଉପରେ ପଥର ଗ୍ଲେସିର୍ ସକ୍ରିୟ ଅଛି |
ଆରିଟିନ୍ଙ୍ଗିଥ୍ ଭାଷା: କ୍ୱିନ୍ସଲ୍ୟାଣ୍ଡର କେପ୍ ୟର୍କରେ ଥରେ ଆରିଟିନ୍ଙ୍ଗିଥ୍ ଏକ ଅଷ୍ଟ୍ରେଲୀୟ ଆଦିବାସୀ ଭାଷା |
ଆରିଟିନ୍ଙ୍ଗିଥ୍ ଭାଷା: କ୍ୱିନ୍ସଲ୍ୟାଣ୍ଡର କେପ୍ ୟର୍କରେ ଥରେ ଆରିଟିନ୍ଙ୍ଗିଥ୍ ଏକ ଅଷ୍ଟ୍ରେଲୀୟ ଆଦିବାସୀ ଭାଷା |
ଆରିଟିନ୍ଙ୍ଗିଥ୍ ଭାଷା: କ୍ୱିନ୍ସଲ୍ୟାଣ୍ଡର କେପ୍ ୟର୍କରେ ଥରେ ଆରିଟିନ୍ଙ୍ଗିଥ୍ ଏକ ଅଷ୍ଟ୍ରେଲୀୟ ଆଦିବାସୀ ଭାଷା |
ଆରିଟିନ୍ଙ୍ଗିଥ୍ ଭାଷା: କ୍ୱିନ୍ସଲ୍ୟାଣ୍ଡର କେପ୍ ୟର୍କରେ ଥରେ ଆରିଟିନ୍ଙ୍ଗିଥ୍ ଏକ ଅଷ୍ଟ୍ରେଲୀୟ ଆଦିବାସୀ ଭାଷା |